No CrossRef data available.
Article contents
A note on rectifiable curves
Published online by Cambridge University Press: 31 October 2008
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let f be a continuous complex-valued function of a real parameter whose real and imaginary parts are of bounded variation in the range (a, b) of the parameter, so that the range of f is a rectifiable plane curve. The main results connecting the arc-length s with the parametrization are as follows:
Theorem 1 (Tonelli). For any rectifiable curve,
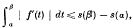
equality holding for all α, β (a ≤ α < β ≤ b) if and only if f is absolutely continuous in (a, b).
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1956


