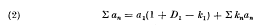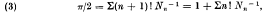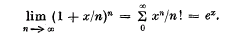Research Article
Colin Maclaurin
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 1-6
-
- Article
-
- You have access
- Export citation
A note on an identity of Jacobi's
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 7-9
-
- Article
-
- You have access
- Export citation
A note on the “probleme des rencontres.”
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 9-12
-
- Article
-
- You have access
- Export citation
A necessary and sufficient condition for differentiability
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 13-16
-
- Article
-
- You have access
- Export citation
On the evaluation of Planck's integral
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 17-20
-
- Article
-
- You have access
- Export citation
Some series for π
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 20-21
-
- Article
-
- You have access
- Export citation
The equal internal bisectors theorem
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 22-23
-
- Article
-
- You have access
- Export citation
A note on equilateral polygons
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 23-24
-
- Article
-
- You have access
- Export citation
On an approximate construction for a regular polygon
-
- Published online by Cambridge University Press:
- 31 October 2008, p. 25
-
- Article
-
- You have access
- Export citation
Euler's limit for ex and the exponential series
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 26-28
-
- Article
-
- You have access
- Export citation
Record of Meetings
Record of Meetings of the Edinburgh Mathematical Society Sixty-fifth Session, 1946–47
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 29-30
-
- Article
-
- You have access
- Export citation
Front matter
MAN volume 37 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2017, p. f1
-
- Article
-
- You have access
- Export citation

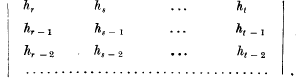 where
where 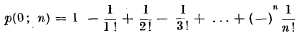 the first
the first 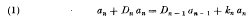
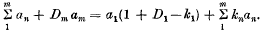 Hence, writing Σ for
Hence, writing Σ for 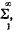 ,
,