Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-06T01:48:17.224Z Has data issue: false hasContentIssue false
  • English
  • Français

An Exact Geometrical Construction for the Exponential Curve

Published online by Cambridge University Press:  31 October 2008

David Robertson
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the curve y = ae−t/t0 (Fig. 1.)

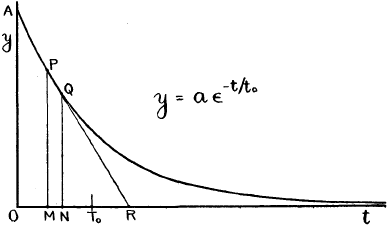
Mark off along the t – axis a distance OT0 equal to the time constant t0.

Divide OT0 into n equal parts and erect ordinates at each point of division.

M, N, are the mth and (m + 1)th of these, counting from O.

MP, NQ, are the corresponding ordinates; P, Q, the points on the curve; and R the intersection of the chord, produced, with the t – axis.

Type
Research Article
Information
Edinburgh Mathematical Notes , Volume 16 , May 1914 , pp. 184 - 186
Copyright
Copyright © Edinburgh Mathematical Society 1914