This paper develops the asymptotic theory for least absolute deviation estimation of a shift in linear regressions. Rates of convergence and asymptotic distributions for the estimated regression parameters and the estimated shift point are derived. The asymptotic theory is developed both for fixed magnitude of shift and for shift with magnitude converging to zero as the sample size increases. Asymptotic distributions are also obtained for trending regressors and for dependent disturbances. The analysis is carried out in the framework of partial structural change, allowing some parameters not to be influenced by the shift. Efficiency relative to least-squares estimation is also discussed. Monte Carlo analysis is performed to assess how informative the asymptotic distributions are.

In this article, we investigate a bias in an asymptotic expansion of the simulated maximum likelihood estimator introduced by Lerman and Manski (pp. 305–319 in C. Manski and D. McFadden (eds.), Structural Analysis of Discrete Data with Econometric Applications, Cambridge: MIT Press, 1981) for the estimation of discrete choice models. This bias occurs due to the nonlinearity of the derivatives of the log likelihood function and the statistically independent simulation errors of the choice probabilities across observations. This bias can be the dominating bias in an asymptotic expansion of the simulated maximum likelihood estimator when the number of simulated random variables per observation does not increase at least as fast as the sample size. The properly normalized simulated maximum likelihood estimator even has an asymptotic bias in its limiting distribution if the number of simulated random variables increases only as fast as the square root of the sample size. A bias-adjustment is introduced that can reduce the bias. Some Monte Carlo experiments have demonstrated the usefulness of the bias-adjustment procedure.

This paper is devoted to a detailed examination of the exact sampling properties of the instrumental variables (IV) estimator of the vector of coefficients on the exogenous variables in a single structural equation. The first two moments of a linear combination of the elements of this estimator and the joint distribution of these elements are considered. Estimable bounds for the first moment that can readily be incorporated into any IV estimation package are provided. The results obtained are in terms of the same special functions as those that characterize other results for this model, allowing a unified treatment of the model.

This paper examines the exact sampling behavior of a family of instrumental variables estimators of the coefficients in a single structural equation when the model has been misspecified by the incorrect inclusion or exclusion of variables. It is found that such specification errors can have implications for the structure of the exact results obtained. A brief numerical examination of the analytical results is also provided.

The definition of causation, discussed in Granger (1980) and elsewhere, has been widely applied in economics and in other disciplines. For this definition, a series yt is said to cause xt+l if it contains information about the forecastability for xt+l contained nowhere else in some large information set, which includes xt−j, j ≥ 0. However, it would be convenient to think of causality being different in extent or direction at seasonal or low frequencies, say, than at other frequencies. The fact that a stationary series is effectively the (uncountably infinite) sum of uncorrelated components, each of which is associated with a single frequency, or a narrow frequency band, introduces the possibility that the full causal relationship can be decomposed by frequency. This is known as the Wiener decomposition or the spectral decomposition of the series, as discussed by Hannan (1970). For any series 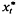generated by 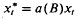, where xt, and 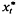are both stationary, with finite variances and a(B) is a backward filter

with B the backward operator, there is a simple, well-known relationship between the spectral decompositions of the two series.

Pötscher (1991, Econometric Theory7, 163–181) has recently considered the question of how the use of a model selection procedure affects the asymptotic distribution of parameter estimators and related statistics. An important potential application of such results is to the generation of confidence regions for the parameters of interest. It is demonstrated that a great deal of care must be exercised in any attempt at such an application. We also consider the effect of model selection on prediction regions. It is demonstrated that the use of asymptotic results for the construction of prediction regions requires the same sort of care as the use of such results for the construction of confidence regions.

In this comment, I first want to offer a few general remarks on the problems caused by nonuniformity in the convergence of coverage probabilities as pointed out in Kabaila's (1995) very stimulating paper. Second, I also argue that within the context of set estimation after model selection one typically will be more interested in conditional coverage probabilities than in unconditional ones. Concentrating on the last example of Section 2 in Kabaila, I then illustrate how a confidence region can be constructed such that the conditional coverage probabilities do not suffer from the nonuniformity problem discussed in Kabaila. As a by-product, I show that the confidence region considered in this example in Kabaila is not a very natural one and that it has undesirable conditional coverage properties, which I find actually more troublesome than the lack of uniformity in the unconditional coverage probability pointed out by Kabaila.

This paper presents a number of consistency results for nonparametric kernel estimators of density and regression functions and their derivatives. These results are particularly useful in semiparametric estimation and testing problems that rely on preliminary nonparametric estimators, as in Andrews (1994, Econometrica 62, 43–72). The results allow for near-epoch dependent, nonidentically distributed random variables, data-dependent bandwidth sequences, preliminary estimation of parameters (e.g., nonparametric regression based on residuals), and nonparametric regression on index functions.