This paper proposes new, simple, and more accurate statistical tests in a cointegrated system that allows for endogenous regressors and serially dependent errors. The approach involves first transforming the time series using orthonormal basis functions in L2[0, 1], which have energy concentrated at low frequencies, and then running an augmented regression based on the transformed data and constructing the test statistics in the usual way. The approach is essentially the same as the trend instrumental variable approach of Phillips (2014), but the number of orthonormal basis functions is held fixed for the development of the standard F and t asymptotic theory. The tests are extremely simple to implement, as they can be carried out in exactly the same way as if the transformed regression is a classical linear normal regression. In particular, critical values are from the standard F or t distribution. The proposed F and t tests are robust in that they are asymptotically valid regardless of whether the number of basis functions is held fixed or allowed to grow with the sample size. The F and t tests have more accurate size in finite samples than existing tests such as the asymptotic chi-squared and normal tests based on the fully modified OLS estimator of Phillips and Hansen (1990) and can be made as powerful as the latter test.

This article revisits the asymptotic inference for nonstationary AR(1) models of Phillips and Magdalinos (2007a) by incorporating a structural change in the AR parameter at an unknown time k0. Consider the model ${y_t} = {\beta _1}{y_{t - 1}}I\{ t \le {k_0}\} + {\beta _2}{y_{t - 1}}I\{ t > {k_0}\} + {\varepsilon _t},t = 1,2, \ldots ,T$, where I{·} denotes the indicator function, one of 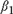${\beta _1}$ and 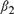${\beta _2}$ depends on the sample size T, and the other is equal to one. We examine four cases: Case (I): 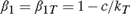${\beta _1} = {\beta _{1T}} = 1 - c/{k_T}$, 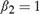${\beta _2} = 1$; (II): 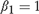${\beta _1} = 1$, 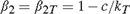${\beta _2} = {\beta _{2T}} = 1 - c/{k_T}$; (III): 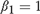${\beta _1} = 1$, 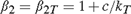${\beta _2} = {\beta _{2T}} = 1 + c/{k_T}$; and case (IV): 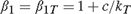${\beta _1} = {\beta _{1T}} = 1 + c/{k_T}$, 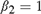${\beta _2} = 1$, where c is a fixed positive constant, and kT is a sequence of positive constants increasing to ∞ such that kT = o(T). We derive the limiting distributions of the t-ratios of 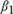${\beta _1}$ and 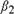${\beta _2}$ and the least squares estimator of the change point for the cases above under some mild conditions. Monte Carlo simulations are conducted to examine the finite-sample properties of the estimators. Our theoretical findings are supported by the Monte Carlo simulations.

In this article, we propose a general method for testing inequality restrictions on nonparametric functions. Our framework includes many nonparametric testing problems in a unified framework, with a number of possible applications in auction models, game theoretic models, wage inequality, and revealed preferences. Our test involves a one-sided version of Lp functionals of kernel-type estimators (1 ≤ p < ∞) and is easy to implement in general, mainly due to its recourse to the bootstrap method. The bootstrap procedure is based on the nonparametric bootstrap applied to kernel-based test statistics, with an option of estimating “contact sets.” We provide regularity conditions under which the bootstrap test is asymptotically valid uniformly over a large class of distributions, including cases where the limiting distribution of the test statistic is degenerate. Our bootstrap test is shown to exhibit good power properties in Monte Carlo experiments, and we provide a general form of the local power function. As an illustration, we consider testing implications from auction theory, provide primitive conditions for our test, and demonstrate its usefulness by applying our test to real data. We supplement this example with the second empirical illustration in the context of wage inequality.

Lieberman and Phillips (2017; LP) introduced a multivariate stochastic unit root (STUR) model, which allows for random, time varying local departures from a unit root (UR) model, where nonlinear least squares (NLLS) may be used for estimation and inference on the STUR coefficient. In a structural version of this model where the driver variables of the STUR coefficient are endogenous, the NLLS estimate of the STUR parameter is inconsistent, as are the corresponding estimates of the associated covariance parameters. This paper develops a nonlinear instrumental variable (NLIV) as well as GMM estimators of the STUR parameter which conveniently addresses endogeneity. We derive the asymptotic distributions of the NLIV and GMM estimators and establish consistency under similar orthogonality and relevance conditions to those used in the linear model. An overidentification test and its asymptotic distribution are also developed. The results enable inference about structural STUR models and a mechanism for testing the local STUR model against a simple UR null, which complements usual UR tests. Simulations reveal that the asymptotic distributions of the NLIV and GMM estimators of the STUR parameter as well as the test for overidentifying restrictions perform well in small samples and that the distribution of the NLIV estimator is heavily leptokurtic with a limit theory which has Cauchy-like tails. Comparisons of STUR coefficient and standard UR coefficient tests show that the one-sided UR test performs poorly against the one-sided STUR coefficient test both as the sample size and departures from the null rise. The results are applied to study the relationships between stock returns and bond spread changes.

The current article examines the limit distribution of the quasi-maximum likelihood estimator obtained from a directionally differentiable quasi-likelihood function and represents its limit distribution as a functional of a Gaussian stochastic process indexed by direction. In this way, the standard analysis that assumes a differentiable quasi-likelihood function is treated as a special case of our analysis. We also examine and redefine the standard quasi-likelihood ratio, Wald, and Lagrange multiplier test statistics so that their null limit behaviors are regular under our model framework.

Limit theory with stochastic integrals plays a major role in time series econometrics. In earlier contributions on weak convergence to stochastic integrals, the literature commonly uses martingale and semi-martingale structures. Liang, Phillips, Wang, and Wang (2016) (see also Wang (2015), Chap. 4.5) currently extended weak convergence to stochastic integrals by allowing for a linear process or a α-mixing sequence in innovations. While these martingale, linear process and α-mixing structures have wide relevance, they are not sufficiently general to cover many econometric applications that have endogeneity and nonlinearity. This paper provides new conditions for weak convergence to stochastic integrals. Our frameworks allow for long memory processes, causal processes, and near-epoch dependence in innovations, which have applications in a wide range of econometric areas such as TAR, bilinear, and other nonlinear models.