Research Article
Noncausality in Continuous Time Models
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 215-256
-
- Article
- Export citation
The Bahadur-Kiefer Representation of Lp Regression Estimators
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 257-283
-
- Article
- Export citation
Laws of Large Numbers for Hilbert Space-Valued Mixingales with Applications
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 284-304
-
- Article
- Export citation
Nonparametric Two-Stage Estimation of Simultaneous Equations with Limited Endogenous Regressors
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 305-330
-
- Article
- Export citation
Valid Edgeworth Expansions of M-Estimators in Regression Models with Weakly Dependent Resfduals
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 331-346
-
- Article
- Export citation
Stochastic Equicontinuity for Unbounded Dependent Heterogeneous Arrays
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 347-359
-
- Article
- Export citation
Gaussian Estimation of a Continuous Time Dynamic Model with Common Stochastic Trends
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 361-373
-
- Article
- Export citation
The Estimation of Continuous Parameter Long-Memory Time Series Models
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 374-390
-
- Article
- Export citation
Photograph Section
ET PHOTOGRAPHS: New Co-Editor
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 391
-
- Article
- Export citation
Notes and Problems
Problems: Kernel Regression with “No” Information
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 393
-
- Article
- Export citation
Problems: Global Concavity of the Likelihood Functions for Two Binary Choice Models
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 393
-
- Article
- Export citation
Problems: Generalization of a Matrix Inequality
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 393-394
-
- Article
- Export citation
Solutions: An Inequality Involving Submatrices
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 394-395
-
- Article
- Export citation
Solutions: Derivation of the OLS Estimator Without Using Calculus
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 395-396
-
- Article
- Export citation
Solutions: An Approximation to GARCH
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 396-401
-
- Article
- Export citation
Solutions: A Mixed-Error Component Model
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 401-402
-
- Article
- Export citation
Solutions: Asymptotic Properties of Tests for Heteroskedasticity under Measurement Error
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 402-403
-
- Article
- Export citation
SOLUTIONS: Asymptotic Local Power of Wald Tests in Untransformed and Transformed Autoregressive Model
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 403-404
-
- Article
- Export citation
SOLUTIONS: Equivalence between OLS and GLS Estimators for Linear Regression Models with AR(1) and MA(1) Errors
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 404
-
- Article
- Export citation
SOLUTIONS: A Simple Expression for the Moore-Penrose Inverse of the Duplication Matrix
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 404
-
- Article
- Export citation

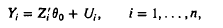
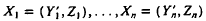 are independent and identically distributed random variables, Y
are independent and identically distributed random variables, Y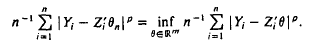
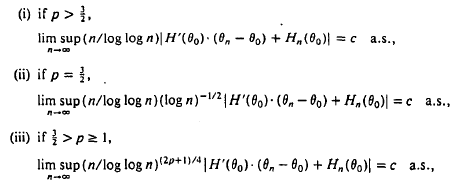
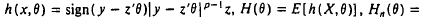
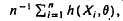 and
and