We consider nonparametric identification and estimation of truncated regression models with unknown conditional heteroskedasticity. The existing methods (e.g., Chen (2010, Review of Economic Studies 77, 127–153)) that ignore heteroskedasticity often result in inconsistent estimators of regression functions. In this paper, we show that both the regression and heteroskedasticity functions are identified in a location-scale setting. Based on our constructive identification results, we propose kernel-based estimators of regression and heteroskedasticity functions and show that the estimators are asymptotically normally distributed. Our simulations demonstrate that our new method performs well in finite samples. In particular, we confirm that in the presence of heteroskedasticity, our new estimator of the regression function has a much smaller bias than Chen’s (2010, Review of Economic Studies 77, 127–153) estimator.

This paper investigates whether there can exist regular estimators in models characterized by nonparametric instrumental variable (NPIV). We show by a number of examples that regular estimation is impossible in general for nonlinear functionals.

Estimation of the intensity of a point process is considered within a nonparametric framework. The intensity measure is unknown and depends on covariates, possibly many more than the observed number of jumps. Only a single trajectory of the counting process is observed. Interest lies in estimating the intensity conditional on the covariates. The impact of the covariates is modelled by an additive model where each component can be written as a linear combination of possibly unknown functions. The focus is on prediction as opposed to variable screening. Conditions are imposed on the coefficients of this linear combination in order to control the estimation error. The rates of convergence are optimal when the number of active covariates is large. As an application, the intensity of the buy and sell trades of the New Zealand Dollar futures is estimated and a test for forecast evaluation is presented. A simulation is included to provide some finite sample intuition on the model and asymptotic properties.

This paper considers linear rational expectations models from the linear systems point of view. Using a generalization of the Wiener-Hopf factorization, the linear systems approach is able to furnish very simple conditions for existence and uniqueness of both particular and generic linear rational expectations models. To illustrate the applicability of this approach, the paper characterizes the structure of stationary and cointegrated solutions, including a generalization of Granger’s representation theorem.

This paper provides sufficient conditions for the nonparametric identification of the regression function 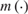$m\left( \cdot \right)$ in a regression model with an endogenous regressor x and an instrumental variable z. It has been shown that the identification of the regression function from the conditional expectation of the dependent variable on the instrument relies on the completeness of the distribution of the endogenous regressor conditional on the instrument, i.e., 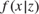$f\left( {x|z} \right)$. We show that (1) if the deviation of the conditional density 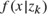$f\left( {x|{z_k}} \right)$ from a known complete sequence of functions is less than a sequence of values determined by the complete sequence in some distinct sequence 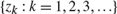$\left\{ {{z_k}:k = 1,2,3, \ldots } \right\}$ converging to 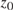${z_0}$, then 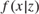$f\left( {x|z} \right)$ itself is complete, and (2) if the conditional density 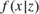$f\left( {x|z} \right)$ can form a linearly independent sequence 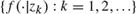$\{ f( \cdot |{z_k}):k = 1,2, \ldots \}$ in some distinct sequence 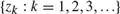$\left\{ {{z_k}:k = 1,2,3, \ldots } \right\}$ converging to 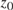${z_0}$ and its relative deviation from a known complete sequence of functions under some norm is finite then $f\left( {x|z} \right)$ itself is complete. We use these general results to provide specific sufficient conditions for completeness in three different specifications of the relationship between the endogenous regressor x and the instrumental variable $z.$

This paper studies the validity of nonparametric tests used in the regression discontinuity design. The null hypothesis of interest is that the average treatment effect at the threshold in the so-called sharp design equals a pre-specified value. We first show that, under assumptions used in the majority of the literature, for any test the power against any alternative is bounded above by its size. This result implies that, under these assumptions, any test with nontrivial power will exhibit size distortions. We next provide a sufficient strengthening of the standard assumptions under which we show that a version of a test suggested in Calonico, Cattaneo, and Titiunik (2014) can control limiting size.