Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T23:56:59.314Z Has data issue: false hasContentIssue false
  • English
  • Français

SEMIPARAMETRIC ESTIMATION OF NONSTATIONARY CENSORED PANEL DATA MODELS WITH TIME VARYING FACTOR LOADS

Published online by Cambridge University Press:  14 May 2008

Songnian Chen  and
Shakeeb Khan
Songnian Chen*
Affiliation:
Hong Kong University of Science and Technology and National University of Singapore
Shakeeb Khan
Affiliation:
Duke University
*
Address correspondence to Songnian Chen, Department of Economics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong; e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose an estimation procedure for a semiparametric panel data censored regression model in which the error terms may be subject to general forms of nonstationarity. Specifically, we allow for heteroskedasticity over time and a time varying factor load on the individual specific effect. Empirically, estimation of this model would be of interest to explore how returns to unobserved skills change over time—see, e.g., Chay (1995, manuscript, Princeton University) and Chay and Honoré (1998, Journal of Human Resources 33, 4–38). 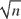We adopt a two-stage procedure based on nonparametric median regression, and the proposed estimator is shown to be -consistent and asymptotically normal. The estimation procedure is also useful in the group effect setting, where estimation of the factor load would be empirically relevant in the study of the intergenerational correlation in income, explored in Solon (1992, American Economic Review 82, 393–408; 1999, Handbook of Labor Economics, vol. 3, 1761–1800) and Zimmerman (1992, American Economic Review 82, 409–429).

Type
Research Article
Information
Econometric Theory , Volume 24 , Issue 5 , October 2008 , pp. 1149 - 1173
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahn, H. & Powell, J.L. (1993) Semiparametric estimation of censored selection models with a nonparametric selection mechanism. Journal of Econometrics 58, 3–29.CrossRefGoogle Scholar
Andrews, D.W.K. (1994) Empirical process methods in econometrics. In Engle, R.F. & McFadden, D. (eds.), Handbook of Econometrics, vol. 4, pp. 2247–2294. North-Holland.Google Scholar
Andrews, D.W.K. & Whang, Y.J. (1990) Additive interactive regression models: Circumvention of the curse of dimensionality. Econometric Theory 6, 466–479.CrossRefGoogle Scholar
Arellano, M. & Honoré, B. (2001) Panel data models: Some recent developments. In Heckman, J.J. & Leamer, E. (eds.), Handbook of Econometrics, vol. 5, pp. 3229–3296. North-Holland.Google Scholar
Ashenfelter, O. & Zimmerman, D.J. (1997) Estimates of returns to schooling from sibling data. Review of Economics and Statistics 79, 1–9.CrossRefGoogle Scholar
Bhattacharya, P.K. & Gangopadhyay, A.K. (1990) Kernel and nearest neighbor estimation of a conditional quantile. Annals of Statistics 18, 1400–1415.CrossRefGoogle Scholar
Buchinsky, M. & Hahn, J. (1998) An alternative estimator for the censored quantile regression model. Econometrica 66, 653–672.CrossRefGoogle Scholar
Chamberlain, G. (1982) Multivariate regression models for panel data. Journal of Econometrics 18, 5–46.CrossRefGoogle Scholar
Chamberlain, G. (1984) Panel data. In Griliches, Z. & Intriligator, M. (eds.), Handbook of Econometrics, vol. 2, pp. 1247–1318. North-Holland.Google Scholar
Chaudhuri, P. (1991a) Nonparametric quantile regression. Annals of Statistics 19, 760–777.CrossRefGoogle Scholar
Chaudhuri, P. (1991b) Global nonparametric estimation of conditional quantiles and their derivatives. Journal of Multivariate Analysis 39, 246–269.CrossRefGoogle Scholar
Chaudhuri, P., Doksum, K., & Samarov, A. (1997) On average derivative quantile regression. Annals of Statistics 25, 715–744.CrossRefGoogle Scholar
Chay, K.Y. (1995) Evaluating the Impact of the 1964 Civil Rights Act on the Economic Status of Black Men Using Censored Longitudinal Earnings Data. Manuscript, Princeton University.Google Scholar
Chay, K.Y. & Honoré, B.E. (1998) Estimation of semiparametric censored regression models. Journal of Human Resources 33, 4–38.CrossRefGoogle Scholar
Chay, K.Y. & Lee, D.S. (2000) Changes in relative wages in the 1980s: Returns to observed and unobserved skills and black-white wage differentials. Journal of Econometrics 99, 1–38.CrossRefGoogle Scholar
Chen, S. (1998) Root-n Consistent Estimation of a Panel Data Sample Selection Model. Manuscript, Hong Kong University of Science and Technology.Google Scholar
Chen, S. & Khan, S. (2000) Estimation of censored regression models in the presence of nonparametric multiplicative heteroskedasticity. Journal of Econometrics 98, 283–316.CrossRefGoogle Scholar
Fan, J. & Gijbels, I. (1996) Local Polynomial Modelling and Its Applications. Chapman and Hall.Google Scholar
Heckman, J.J. (1981) Statistical models for discrete panel data. In McFadden, D. & Manski, C. (eds.), Structural Analysis of Discrete Data with Econometric Applications. MIT Press.Google Scholar
Heckman, J.J. & MaCurdy, T.E. (1980) A life cycle model of female labor supply. Review of Economic Studies 47, 47–74.CrossRefGoogle Scholar
Holtz-Eakin, D., Newey, W.K., & Rosen, H.S. (1988) Estimating vector autoregressions with panel data. Econometrica 56, 1371–1395.CrossRefGoogle Scholar
Honoré, B.E. (1992) Trimmed LAD and least squares estimation of truncated and censored regression models with fixed effects. Econometrica 60, 533–565.CrossRefGoogle Scholar
Honoré, B.E. (1998) IV Estimation of Panel Data Tobit Models with Normal Errors. Working paper, Princeton University.Google Scholar
Honoré, B.E., Khan, S., & Powell, J.L. (2002) Quantile regression under random censoring. Journal of Econometrics 109, 67–105.CrossRefGoogle Scholar
Honoré, B.E. & Kyriazidou, E. (2000) Estimation of Tobit-type models with individual specific effects. Econometric Reviews 19, 341–366.CrossRefGoogle Scholar
Honoré, B.E., Kyriazidou, E., & Udry, C. (1997) Estimation of type 3 Tobit models using symmetric trimming and pairwise comparisons. Journal of Econometrics 76, 107–128.CrossRefGoogle Scholar
Honoré, B.E. & Lewbel, A. (2002) Semiparametric binary choice panel data models without strictly exogeneous regressors. Econometrica 70, 2053–2063.CrossRefGoogle Scholar
Hsiao, C. (1986) Analysis of Panel Data. Cambridge University Press.Google Scholar
Khan, S. (2001) Two stage rank estimation of quantile index models. Journal of Econometrics 100, 319–355.CrossRefGoogle Scholar
Khan, S. & Powell, J.L. (2001) Two-step quantile estimation of semiparametric censored regression models. Journal of Econometrics 103, 73–110.CrossRefGoogle Scholar
Koenker, R. & Bassett, G.S. Jr. (1978) Regression quantiles. Econometrica 46, 33–50.CrossRefGoogle Scholar
Koenker, R., Ng, P., & Portnoy, S. (1994) Quantile smoothing splines. Biometrika 81, 673–680.CrossRefGoogle Scholar
Koenker, R., Portnoy, S., & Ng, P. (1992) Nonparametric estimation of conditional quantile function. In Dodge, Y. (ed.), Proceedings of the Conference on L 1-Statistical Analysis and Related Methods, pp. 217–229. Elsevier.Google Scholar
Kyriazidou, E. (1997) Estimation of a panel data sample selection model. Econometrica 65, 1335–1364.CrossRefGoogle Scholar
Manski, C.F. (1987) Semiparametric analysis of random effects linear models from binary panel data. Econometrica 55, 357–362.CrossRefGoogle Scholar
Newey, W.K. (1994) The asymptotic variance of semiparametric estimators. Econometrica 62, 1349–1382.CrossRefGoogle Scholar
Newey, W.K. & McFadden, D. (1994) Large sample estimation and hypothesis testing. In Engle, R.F. & McFadden, D. (eds.), Handbook of Econometrics, vol. 4. North-Holland.Google Scholar
Nijman, T. & Verbeek, M. (1992) Nonresponse in panel data: The impact on estimates of a life cycle consumption function. Journal of Applied Econometrics 7, 243–257.CrossRefGoogle Scholar
Powell, J.L. (1984) Least absolute deviations estimation for the censored regression model. Journal of Econometrics 25, 303–325.CrossRefGoogle Scholar
Powell, J.L. (1986) Censored regression quantiles. Journal of Econometrics 32, 143–155.CrossRefGoogle Scholar
Powell, J.L., Stock, J.H., & Stoker, T.M. (1989) Semiparametric estimation of index coefficients. Econometrica 57, 1404–1430.CrossRefGoogle Scholar
Solon, G. (1992) Intergenerational income mobility in the United States. American Economic Review 82(3), 393–408.Google Scholar
Solon, G. (1999) Intergenerational mobility in the labor market. In Ashenfelter, O. & Card, D. (eds.), Handbook of Labor Economics, vol. 3, pp. 1761–1800. North-Holland.Google Scholar
Stone, C.J. (1985) Additive regression and other nonparametric models. Annals of Statistics 13, 689–705.CrossRefGoogle Scholar
Stute, W. (1986) Conditional empirical processes. Annals of Statistics 14, 638–647.CrossRefGoogle Scholar
Tobin, J. (1958) Estimation of relationships for limited dependent variables. Econometrica 26, 24–36.CrossRefGoogle Scholar
Troung, Y. (1989) Asymptotic properties of kernel estimates based on local medians. Annals of Statistics 17, 606–617.Google Scholar
Verbeek, M. & Nijman, T. (1992) Testing for selectivity bias in panel data models. International Economics Review 33, 681–703.CrossRefGoogle Scholar
Weiss, A.A. (1993) Some aspects of measurement error in a censored regression model. Journal of Econometrics 56, 169–188.CrossRefGoogle Scholar
Zabel, J. (1992) Estimating fixed and random effects models with selectivity. Economic Letters 40, 269–272.CrossRefGoogle Scholar
Zimmerman, D.J. (1992) Regression towards mediocrity in economic stature. American Economic Review 82, 409–429.Google Scholar