Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T23:39:46.330Z Has data issue: false hasContentIssue false
  • English
  • Français

LIMIT THEORY FOR EXPLOSIVELY COINTEGRATED SYSTEMS

Published online by Cambridge University Press:  04 April 2008

Peter C.B. Phillips  and
Tassos Magdalinos
Peter C.B. Phillips*
Affiliation:
Cowles Foundation for Research in Economics, Yale University, University of Auckland and University of York
Tassos Magdalinos
Affiliation:
University of Nottingham
*
Address correspondence to Peter C.B. Phillips, Department of Economics, Yale University, P.O. Box 208268, New Haven, CT 06520-8268, USA; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

A limit theory is developed for multivariate regression in an explosive cointegrated system. The asymptotic behavior of the least squares estimator of the cointegrating coefficients is found to depend upon the precise relationship between the explosive regressors. When the eigenvalues of the autoregressive matrix Θ are distinct, the centered least squares estimator has an exponential Θn rate of convergence and a mixed normal limit distribution. No central limit theory is applicable here, and Gaussian innovations are assumed. On the other hand, when some regressors exhibit common explosive behavior, a different mixed normal limiting distribution is derived with rate of convergence reduced to . 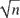In the latter case, mixed normality applies without any distributional assumptions on the innovation errors by virtue of a Lindeberg type central limit theorem. Conventional statistical inference procedures are valid in this case, the stationary convergence rate dominating the behavior of the least squares estimator.

Type
Research Article
Information
Econometric Theory , Volume 24 , Issue 4 , August 2008 , pp. 865 - 887
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abadir, K.M. ’ Magnus, J.R. (2005) Matrix Algebra. Econometric Exercises, vol. 1. Cambridge University Press.CrossRefGoogle Scholar
Anderson, T.W. (1959) On asymptotic distributions of estimates of parameters of stochastic difference equations. Annals of Mathematical Statistics 30, 676–687.CrossRefGoogle Scholar
Hall, P. ’ Heyde, C.C. (1980) Martingale Limit Theory and Its Application. Academic Press.Google Scholar
Magdalinos, T. ’ Phillips, P.C.B. (2006) Limit Theory for Cointegrated Systems with Moderately Integrated and Moderately Explosive Regressors. Working paper, Yale University.Google Scholar
Mijnheer, J. (2002) Asymptotic inference for AR(1) processes with (nonnormal) stable innovations, part V: The explosive case. Journal of Mathematical Sciences 111, 3854–3856.CrossRefGoogle Scholar
Park, J.Y. ’ Phillips, P.C.B. (1988) Statistical inference in regressions with integrated processes, part 1. Econometric Theory 4, 468–497.CrossRefGoogle Scholar
Park, J.Y. ’ Phillips, P.C.B. (1989) Statistical inference in regressions with integrated processes, part 2. Econometric Theory 5, 95–131.CrossRefGoogle Scholar
Phillips, P.C.B. (1985) The distribution of matrix quotients. Journal of Multivariate Analysis 16, 157–161.CrossRefGoogle Scholar
White, J.S. (1958) The limiting distribution of the serial correlation coefficient in the explosive case. Annals of Mathematical Statistics 29, 1188–1197.CrossRefGoogle Scholar