Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T18:11:27.676Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGHER ORDER ASYMPTOTIC THEORY FOR MINIMUM CONTRAST ESTIMATORS OF SPECTRAL PARAMETERS OF STATIONARY PROCESSES

Published online by Cambridge University Press:  24 September 2003

Masanobu Taniguchi ,
Kees Jan van Garderen  and
Madan L. Puri
Masanobu Taniguchi
Affiliation:
Waseda University
Kees Jan van Garderen
Affiliation:
University of Amsterdam and Indiana University
Madan L. Puri
Affiliation:
University of Amsterdam and Indiana University
Get access Rights & Permissions [Opens in a new window]

Abstract

Let g(λ) be the spectral density of a stationary process and let fθ(λ), θ ∈ Θ, be a fitted spectral model for g(λ). A minimum contrast estimator 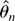of θ is defined that minimizes a distance 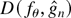between 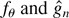, where 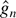is a nonparametric spectral density estimator based on n observations. It is known that 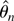is asymptotically Gaussian efficient if g(λ) = fθ(λ). Because there are infinitely many candidates for the distance function 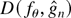, this paper discusses higher order asymptotic theory for 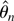in relation to the choice of D. First, the second-order Edgeworth expansion for 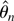is derived. Then it is shown that the bias-adjusted version of 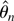is not second-order asymptotically efficient in general. This is in sharp contrast with regular parametric estimation, where it is known that if an estimator is first-order asymptotically efficient, then it is automatically second-order asymptotically efficient after a suitable bias adjustment (e.g., Ghosh, 1994, Higher Order Asymptotics, p. 57). The paper establishes therefore that for semiparametric estimation it does not hold in general that “first-order efficiency implies second-order efficiency.” The paper develops verifiable conditions on D that imply second-order efficiency.This paper was written while the first author was visiting the University of Bristol as a Benjamin Meaker Professor. The second author was previously at Bristol and is now supported by a fellowship of the Royal Netherlands Academy of Arts and Sciences. We are grateful to the co-editor Pentti Saikkonen and two anonymous referees for their valuable comments, which significantly improved the paper.

Type
Research Article
Information
Econometric Theory , Volume 19 , Issue 6 , December 2003 , pp. 984 - 1007
Copyright
© 2003 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akahira, M. (1986) The Structure of Asymptotic Deficiency of Estimators. Queen's Papers in Pure and Applied Mathematics 75, Ontario.
Albrecht, V. (1983) On the convergence rate of probability of error in Bayesian discrimination between two Gaussian processes. Asymptotic Statistics, vol. 2, Proceedings of the Third Prague Symposium on Asymptotic Statistics, pp. 165–175. Amsterdam: Elsevier.
Bentkus, R.Y. & R.A. Rudzkis (1982) On the distribution of some statistical estimates of spectral density. Theory of Probability and Its Applications 27, 795–814.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. New York: Wiley.
Bloomfield, P. (1973) An exponential model for the spectrum of a scalar time series. Biometrika 60, 217–226.Google Scholar
Brillinger, D.R. (1981) Time Series: Data Analysis and Theory, expanded ed. San Francisco: Holden-Day.
Dahlhaus, R. & W. Wefelmeyer (1996) Asymptotically optimal estimation in misspecified time series models. Annals of Statistics 24, 952–974.Google Scholar
Ghosh, J.K. (1994) Higher Order Asymptotics. California: Institute of Mathematical Statistics.
Hannan, E.J. (1963) Regression for time series. In M. Rosenblatt (ed.), Time Series Analysis, pp. 17–37. New York: Wiley.
Hannan, E.J. (1970) Multiple Time Series. New York: Wiley.
Hosoya, Y. & M. Taniguchi (1982) A central limit theorem for stationary processes and the parameter estimation for linear processes. Annals of Statistics 10, 132–153. Correction: (1993): 21, 1115–1117.Google Scholar
Hua, L. & C. Ping (1993) Second order asymptotic efficiency in a partially linear model. Statistics and Probability Letters 18, 73–84.Google Scholar
Kakizawa, Y., R.H. Shumway, & M. Taniguchi (1998) Discrimination and clustering for multivariate time series. Journal of the American Statistical Association 93, 328–340.Google Scholar
Nishiyama, Y. & P.M. Robinson (2000) Edgeworth expansions for semiparametric averaged derivatives. Econometrica 68, 931–979.Google Scholar
Robinson, P.M. (1995) The normal approximation for semiparametric averaged derivatives. Econometrica 63, 667–680.Google Scholar
Taniguchi, M. (1979) On estimation of parameters of Gaussian stationary processes. Journal of Applied Probability 16, 575–591.Google Scholar
Taniguchi, M. (1981) An estimation procedure of parameters of a certain spectral density model. Journal of the Royal Statistical Society, Series B 43, 34–40.Google Scholar
Taniguchi, M. (1987) Minimum contrast estimation for spectral densities of stationary processes. Journal of the Royal Statistical Society, Series B 49, 315–325.Google Scholar
Taniguchi, M. (1991) Higher Order Asymptotic Theory for Time Series Analysis. Lecture Notes in Statistics, vol. 68. Heidelberg: Springer-Verlag.
Taniguchi, M. & Y. Kakizawa (2000) Asymptotic Theory of Statistical Inference for Time Series. New York: Springer-Verlag.
Velasco, C. & P.M. Robinson (2001) Edgeworth expansions for spectral density estimates and studentized sample mean. Econometric Theory 17, 497–539.Google Scholar
Xiao, Z. & P.C.B. Phillips (1998) Higher order approximations for frequency domain time series regression. Journal of Econometrics 86, 297–336.Google Scholar
Zhang, G. & M. Taniguchi (1995) Nonparametric approach for discriminant analysis in time series. Journal of Nonparametric Statistics 5, 91–101.Google Scholar
Zygmund, A. (1959) Trigonometric Series. London: Cambridge University Press.