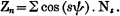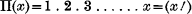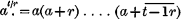Research Article
I.—Observations upon the Structure of a Genus of Oligochœta belonging to the Limicoline Section
-
- Published online by Cambridge University Press:
- 17 January 2013, pp. 1-17
-
- Article
- Export citation
II.—On the Transformation of Laplace's Coefficients
-
- Published online by Cambridge University Press:
- 17 January 2013, pp. 19-43
-
- Article
- Export citation
III.—Phases of the Living Greek Language
-
- Published online by Cambridge University Press:
- 17 January 2013, pp. 45-55
-
- Article
- Export citation
IV.—Adamantios Koraes, and his Reformation of the Greek Language
-
- Published online by Cambridge University Press:
- 17 January 2013, pp. 57-61
-
- Article
- Export citation
V.—On the Fossil Flora of the Staffordshire Coal Fields
-
- Published online by Cambridge University Press:
- 17 January 2013, pp. 63-98
-
- Article
- Export citation
VI.—The Solar Spectrum at Medium and Low Altitudes. Observations of the Region between Wave-Lengths 6024 and 4861 Å.U., made at Lord Crawford's Observatory, Dun Echt, during the Years 1887 to 1889
-
- Published online by Cambridge University Press:
- 17 January 2013, pp. 99-210
-
- Article
- Export citation
VII.—Electrolytic Synthesis of Dibasic Acids
-
- Published online by Cambridge University Press:
- 17 January 2013, pp. 211-224
-
- Article
- Export citation
VIII.—On Impact
-
- Published online by Cambridge University Press:
- 17 January 2013, pp. 225-252
-
- Article
- Export citation
Front matter
TRE volume 36 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 17 January 2013, pp. f1-f7
-
- Article
-
- You have access
- Export citation