No CrossRef data available.
Published online by Cambridge University Press: 17 January 2013
The development of the inverse square root
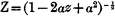
into a series
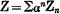
gives rise to the coefficients Zn, which have been called “Laplace's Coefficients” If in Zn we substitute for z the expression

where
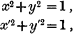
then the function of ψ, which Zn will represent, can most appropriately be expressed by

The object of this paper is to show, by actual calculation, that the coefficients Ns, (functions of x, x′, y, y′) can be worked out by elementary algebraical processes, the only auxiliary taken from higher analysis being the expression of the powers of cos ψ in function of the cosines of the multiples of ψ.
As to our notations, we shall observe throughout the following restrictions:—
1. The function Π(x) shall not be employed otherwise than for integer positive values of x, so that
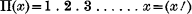
2. The factorial
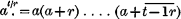
will be made use of for integer values only of r (as, for example, r = + 1, or r = − 1, or r = + 2, &c., the exponent t being integer positive.
page 29 note * Commentationes Societatis Goettingensis recentiores, to. ii., anno 1812.