Impact Statement
Data-centric engineering considers telemetry data from populations of systems with increasingly complex interdependencies. This work introduces a Bayesian approach to represent the relationships between aggregate systems, via multilevel models, similar to deep Gaussian processes. Considering the population as a whole, the value of data is extended and knowledge of underlying physics can be incorporated within models and between models. By leveraging information between domains, the combined model is used for transfer learning and predicts the characteristics (hyperparameters) of systems that were previously unobserved.
1. Introduction: Multilevel models for meta-modelling
Increasingly, engineering systems are equipped with sensors, often providing streams of telemetry data. As the number of instrumented systems grows, population data become available [Reference Gardner, Bull, Gosliga, Dervilis, Cross, Papatheou and Worden1]. While machine populations clearly differ from the natural examples in ecology, epidemiology, and behavioural science, the same statistical methods can be used to represent artificial systems [Reference Rahwan, Cebrian, Obradovich, Bongard, Bonnefon, Breazeal, Christakis, Couzin, Jackson, Jennings, Kamar, Kloumann, Larochelle, Lazer, McElreath, Mislove, Parkes, Pentland, Roberts, Shariff, Tenenbaum and Wellman2].
In this article, we consider multilevel (or hierarchical) models [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3] which are particularly suited to population data, as they naturally exhibit a hierarchical structure. As an engineering example, consider turbines of the same specification in a wind farm. Each individual is unique, with its own wind-power relationship, depending on the local environment. On the other hand, some parameters are shared between operating subgroups (e.g. maximum power) while others are global (e.g. the minimum rpm to generate power).
A multilevel model can represent interdependent population data via partial pooling [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3] where parameter hierarchies are learnt with machine-specific and shared parameters (or functions). As such, models share (i.e. pool) information, to extend the value of data. Multilevel models are often termed multitask learners, as multiple related tasks
![]() $ {f}_k $
are learnt simultaneously to improve inference [Reference Murphy4]. Figure 1 visualises how multilevel models can learn multiple tasks.
$ {f}_k $
are learnt simultaneously to improve inference [Reference Murphy4]. Figure 1 visualises how multilevel models can learn multiple tasks.

Figure 1. A visual example of multilevel models for multitask learning: predictive tasks
![]() $ {f}_k $
are parametrised by
$ {f}_k $
are parametrised by
![]() $ {\theta}_k=\left\{{\theta}_k^{\prime },{\theta}_k^{{\prime\prime}}\right\} $
or
$ {\theta}_k=\left\{{\theta}_k^{\prime },{\theta}_k^{{\prime\prime}}\right\} $
or
![]() $ {\theta}_k=\left\{{\theta}_k^{\prime },{\theta}_k^{{\prime\prime\prime}}\right\} $
; in turn,
$ {\theta}_k=\left\{{\theta}_k^{\prime },{\theta}_k^{{\prime\prime\prime}}\right\} $
; in turn,
![]() $ {\theta}_k $
is generated by shared intertask functions
$ {\theta}_k $
is generated by shared intertask functions
![]() $ \left\{{g}^{\prime },{g}^{{\prime\prime}}\right\} $
or
$ \left\{{g}^{\prime },{g}^{{\prime\prime}}\right\} $
or
![]() $ \left\{{g}^{\prime },{g}^{{\prime\prime\prime}}\right\} $
. The notation
$ \left\{{g}^{\prime },{g}^{{\prime\prime\prime}}\right\} $
. The notation
![]() $ g\to \theta $
shows a function g that predicts a parameter
$ g\to \theta $
shows a function g that predicts a parameter
![]() $ \theta $
.
$ \theta $
.
With interpretable models, one can inspect how parameters
![]() $ {\theta}_k $
vary between tasks. These variations are termed intertask relationships, and each function that approximates them (shown as g in Figure 1) can be considered as a meta-model (a model of models). If desired, these intertask functions can be built to vary with respect to higher-level (macro) explanatory variables. A simple example is the varying coefficients model, typically demonstrated with the 8-schools data [Reference Kreft and De Leeuw5]. Intertask relationships are useful in engineering practice, as they allow alternative insights to be extracted from collected population data.
$ {\theta}_k $
vary between tasks. These variations are termed intertask relationships, and each function that approximates them (shown as g in Figure 1) can be considered as a meta-model (a model of models). If desired, these intertask functions can be built to vary with respect to higher-level (macro) explanatory variables. A simple example is the varying coefficients model, typically demonstrated with the 8-schools data [Reference Kreft and De Leeuw5]. Intertask relationships are useful in engineering practice, as they allow alternative insights to be extracted from collected population data.
1.1. Source localisation
This work considers a population where members are represented by a sequence of 28 Acoustic Emission (AE) experiments, originally from [Reference Hensman, Mills, Pierce, Worden and Eaton6]. In each experiment, the arrival time of waves propagating through a complex plate geometry is recorded. For each dataset, a 2D map of the arrival times is learnt through regression. Despite distinct experiment designs, the metal plate remains consistent (the medium through which waves propagate) suggesting that their models share certain parameters. By analysing these datasets collectively, as a population, additional insights are extracted from the test campaign. We capture how characteristics of the 2D map vary, allowing predictions of hyperparameters for the response surface of experimental designs that were absent from the training data. In other words, one can extrapolate or interpolate in the model space by using the intertask functions as meta-models, to predict hyperparameters. Because of the plate’s complexity, we encode weak constraints on the model given domain expertise of the experimental campaign, rather than specific physics-based laws (e.g. via differential equations).
These insights have significant implications since the meta-models can be used to predict the characteristics of the response (hyperparameters) for new, previously unobserved experimental designs. Such model predictions alleviate the requirement of extensive training data in new tasks, by sharing information from similar experiments. The result is an interpretable and explainable approach to transfer learning for engineering experiments.
1.2. Layout
Section 2 introduces the AE data, the experimental campaign, and their multilevel interpretation. Section 3 uses Gaussian Process regression for a single AE experiment. Section 4 extends the model to represent data from the full test campaign in a joint inference, investigating different model assumptions and the associated intertask relationships. Section 5 assesses the predictive performance and utilises the model for transfer learning. Section 6 offers concluding remarks.
1.3. Related Work & Contribution
To improve interpretability and ensure meaningful outputs from data-driven models, the inclusion of physical insight within machine learning methods is becoming increasingly popular, with overviews found in [Reference Karniadakis, Kevrekidis, Lu, Perdikaris, Wang and Yang7, Reference Willard, Jia, Xu, Steinbach and Kumar8]. These approaches are often referred to as physics-informed machine learning, since they utilise both data and explanatory physics to improve modelling when compared to either approach independently. Some examples include physics-guided loss functions [Reference Daw, Karpatne, Watkins, Read and Kumar9], vector field constraints [Reference Wahlström, Kok, Schön and Gustafsson10], and the inclusion of governing differential equations [Reference Alvarez, Luengo and Lawrence11]. Given the complexity of the plate geometry in this work, the physics-based constraints are soft, since any predictive functions can deviate from the suggested structure. To achieve this, a Bayesian approach is used, where the constraints are placed on a (hierarchical) prior distribution [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3], which offers a natural trade-off between prior knowledge and data. While this trade-off is possible with a (weighted) physics-guided loss function, we favour a hierarchical statistical approach for uncertainty quantification and interpretability when multitask learning.
Contribution In the context of AE (time of arrival) mapping, previous work of (coauthors) Jones et al. [Reference Jones, Rogers and Cross12] considered how domain knowledge can be encoded in Gaussian Process (GP) models via boundary condition constraints, applied to the kernel function for a single experiment. Here, we extend the work to represent multiple experiments, allowing us to encode domain expertise at the systems level and infer intertask relationships for a series of testsFootnote 1. Our key contribution is the ability to encode physics-based knowledge between tasks, as well as within tasks. Rather than a single experiment, the resultant model represents variations over collected tests in an experimental campaign: this allows for simulation and (hyper) parameter prediction at previously unobserved experimental designs (in this case, sensor separation).
A multilevel modeling approach is adopted, which is increasingly utilized in the engineering literature. An early monitoring example is presented by Huang et al. [Reference Huang, Beck and Li13] and Huang and Beck [Reference Huang and Beck14], where multiple correlated regression tasks are utilized for modal analysis. A shared sparsity profile is inferred for tasks relating to measurement channels to improve damage detection by considering the correlation between damage scenarios or adjacent sensors. More recent applications include Di Francesco et al. [Reference Di Francesco, Chryssanthopoulos, Faber and Bharadwaj15] who use multilevel models to represent corrosion progression given evidence from multiple locations, and Papadimas and Dodwell [Reference Papadimas and Dodwell16], where the results from materials tests (that is coupon samples) are combined to inform the estimation of material properties. Similar to Papadimas and Dodwell [Reference Papadimas and Dodwell16] our work considers an experimental campaign, but rather than infer the higher-level representation as a global estimate of a single experiment, we introduce inter-task explanatory variables. In turn, the model represents task variations as functions, rather than uni-modal sampling distributions.
On a related theme, Hughes et al. [Reference Hughes, Gardner and Worden17] recognize structures and their populations as nested hierarchies, proposing a convenient formulation for decision analyses. Sedehi et al. [Reference Sedehi, Kosikova, Papadimitriou and Katafygiotis18] also present work to encode physics into hierarchical GPs, where time-history measurements are partitioned into multiple segments to create longitudinal data, accounting for temporal variability and addressing the non-stationarity of the measured responses for a single structure.
2. The AE experiments
AE are ultrasonic signals released within a material as its internal structure undergoes some irreversible change. The driving mechanisms often relate to the initiation and growth of damage, so monitoring AE signals can serve to assess the condition of materials and structures [Reference Shull19]. As emissions propagate through material from the point of origin, differences in the time of arrival at separate sensors (in an array) can be used for triangulation (or trilateration) to enable source localization [Reference Tobias20]. From a damage monitoring perspective, source localization provides an operator with more insight to make better maintenance and planning decisions.
One strategy for localizing AE signals involves learning the map of the arrival times across the surface of interest [Reference Jones, Rogers, Worden and Cross21]. That is, the forward mapping from AE source localization
![]() $ {\mathbf{x}}_i $
to the measured difference in time-of-arrival (
$ {\mathbf{x}}_i $
to the measured difference in time-of-arrival (
![]() $ \Delta $
ToA) for a given sensor pair,
$ \Delta $
ToA) for a given sensor pair,
where
![]() $ {y}_i $
is some noisy observation of
$ {y}_i $
is some noisy observation of
![]() $ \Delta $
ToA with additive observation noise
$ \Delta $
ToA with additive observation noise
![]() $ {\unicode{x025B}}_i $
. In this paper, we consider data from experiments by Hensman et al. [Reference Hensman, Mills, Pierce, Worden and Eaton6] concerning an aluminum plate-like structure shown in Figure 2.
$ {\unicode{x025B}}_i $
. In this paper, we consider data from experiments by Hensman et al. [Reference Hensman, Mills, Pierce, Worden and Eaton6] concerning an aluminum plate-like structure shown in Figure 2.
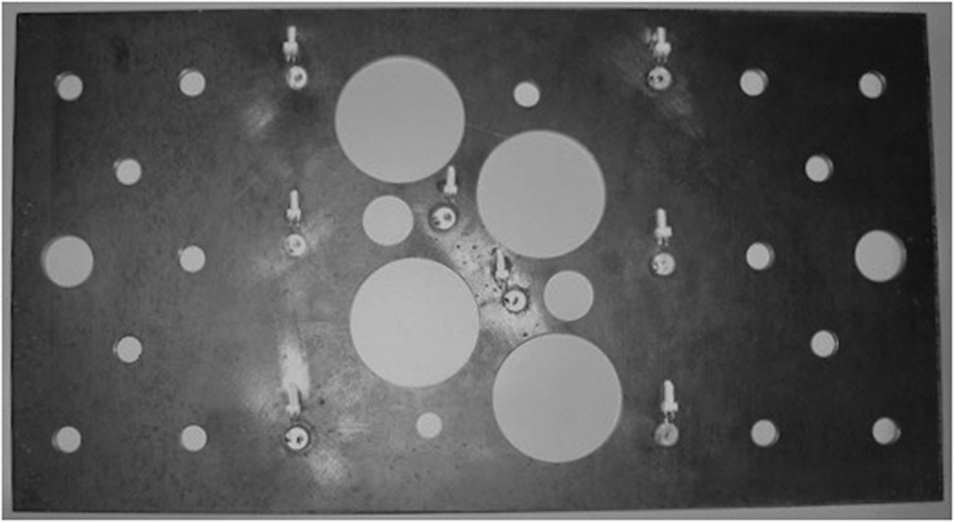
Figure 2. Image of plate used in the AE experiments.
Artificial AEs were excited by thermoelastic expansion generated with an incident laser pulse, with the signals captured at eight piezoceramic (Sonox P5) sensors mounted to the surface of the plate, visible in Figure 2 and shown by the black markers in Figure 3, numbered 1–8 (left). The sensors operate by converting surface displacements resulting from the AE stress waves into electrical energy, allowing the ultrasonic signals to be captured digitally. There are a total of N = 2,227 possible source locations, shown by blue markers in Figure 3 (left). The time of arrival for each of the eight sensors was extracted following standard practice, using an autoregressive form of the Akaike Information Criterion (AIC) [Reference Hensman, Mills, Pierce, Worden and Eaton6].
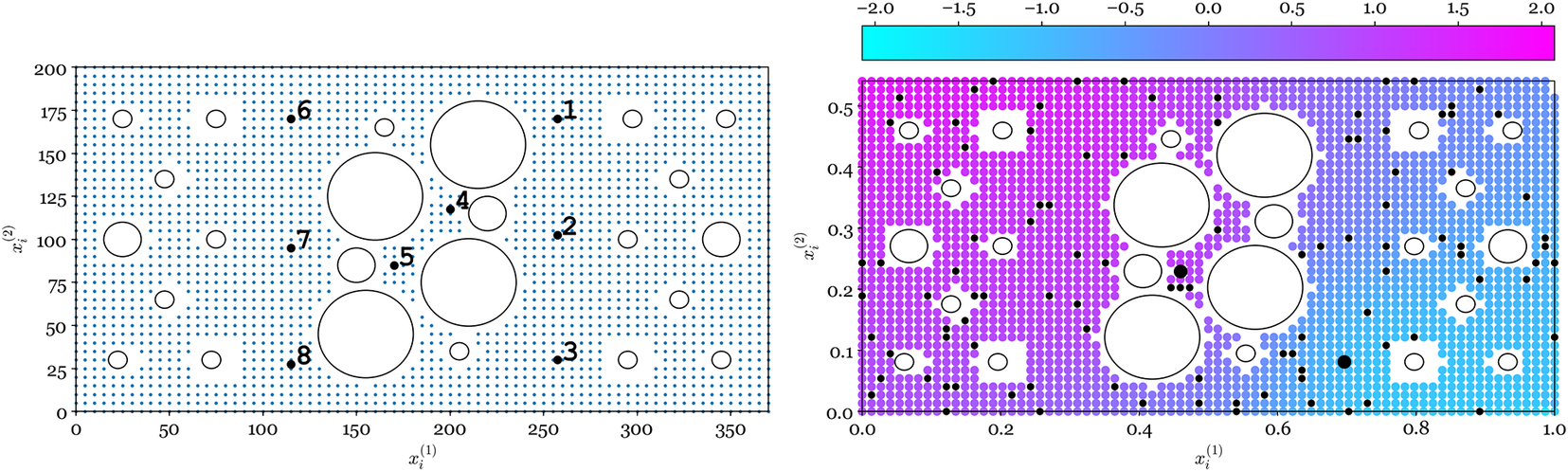
Figure 3. Left: all source locations (blue
![]() $ \bullet $
) and sensor locations (black
$ \bullet $
) and sensor locations (black
![]() $ \bullet $
). Right: heatmap of the
$ \bullet $
). Right: heatmap of the
![]() $ \Delta $
ToA (response
$ \Delta $
ToA (response
![]() $ {y}_i $
) given locations (inputs
$ {y}_i $
) given locations (inputs
![]() $ {\mathbf{x}}_i=\left\{{x}_i^{(1)},{x}_i^{(2)}\right\} $
) for the experiment
$ {\mathbf{x}}_i=\left\{{x}_i^{(1)},{x}_i^{(2)}\right\} $
) for the experiment
![]() $ k=15 $
, sensor pair (Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3, Reference Kreft and De Leeuw5).
$ k=15 $
, sensor pair (Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3, Reference Kreft and De Leeuw5).
2.1. Difference in time-of-arrival (
 $ \Delta $
ToA)
$ \Delta $
ToA)
Let the arrival time of AE
![]() $ i $
at sensor
$ i $
at sensor
![]() $ j $
be denoted
$ j $
be denoted
![]() $ {A}_{ij}\hskip1em \forall j\in \left\{1,2,\dots, 8\right\} $
. The difference in time-of-arrival (
$ {A}_{ij}\hskip1em \forall j\in \left\{1,2,\dots, 8\right\} $
. The difference in time-of-arrival (
![]() $ \Delta $
ToA) is then the difference between any two sensors. Since there are eight sensors, there are 28 pairwise combinations and associated maps (8C2). Each pair generates a different
$ \Delta $
ToA) is then the difference between any two sensors. Since there are eight sensors, there are 28 pairwise combinations and associated maps (8C2). Each pair generates a different
![]() $ f $
(distinguished with notation later). For example, the pair (Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3, Reference Kreft and De Leeuw5) would present the scalar output
$ f $
(distinguished with notation later). For example, the pair (Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3, Reference Kreft and De Leeuw5) would present the scalar output
![]() $ {y}_i\in \mathrm{\mathbb{R}} $
,
$ {y}_i\in \mathrm{\mathbb{R}} $
,
![]() $ {y}_i={A}_{i3}-{A}_{i5} $
. The input vectors
$ {y}_i={A}_{i3}-{A}_{i5} $
. The input vectors
![]() $ {\mathbf{x}}_i\in {\mathrm{\mathbb{R}}}^2 $
are the locations (length versus width),
$ {\mathbf{x}}_i\in {\mathrm{\mathbb{R}}}^2 $
are the locations (length versus width),
![]() $ {\mathbf{x}}_i=\left\{{x}_i^{(1)},{x}_i^{(2)}\right\} $
where {0, 0} is the bottom left corner of the plate. Figure 3 (right) shows the data associated with the sensor pair (Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3, Reference Kreft and De Leeuw5) while Figure 4 shows all pairs. Each combination is labelled with an experiment index
$ {\mathbf{x}}_i=\left\{{x}_i^{(1)},{x}_i^{(2)}\right\} $
where {0, 0} is the bottom left corner of the plate. Figure 3 (right) shows the data associated with the sensor pair (Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3, Reference Kreft and De Leeuw5) while Figure 4 shows all pairs. Each combination is labelled with an experiment index
![]() $ k\in \left\{1,2\dots, 28\right\} $
listed in Table 2 Appendix B.
$ k\in \left\{1,2\dots, 28\right\} $
listed in Table 2 Appendix B.

Figure 4. Heatmaps of the measured
![]() $ \Delta $
ToA (
$ \Delta $
ToA (
![]() $ {y}_i $
) with respect to locations (
$ {y}_i $
) with respect to locations (
![]() $ {\mathbf{x}}_i $
) for all sensor combinations. Large black markers plot sensor pairs, while small black markers plot training observations. The remaining data are used to test out-of-sample performance. The number in the bottom right is the experiment index
$ {\mathbf{x}}_i $
) for all sensor combinations. Large black markers plot sensor pairs, while small black markers plot training observations. The remaining data are used to test out-of-sample performance. The number in the bottom right is the experiment index
![]() $ k\in \left\{1,2,\dots \mathrm{28}\right\} $
.
$ k\in \left\{1,2,\dots \mathrm{28}\right\} $
.
2.2. A note on normalization
Figure 4 plots
![]() $ N=100 $
training data for each sensor pair combination, sampled uniformly from each task. We then normalize inputs with respect to the longest edge, such that the plate’s length is unity. This scaling maintains approximately the same relative smoothness of the map in each direction, that is one length scale for both dimensions. Rather than normalize the response for each plate independently, it is z-score normalized with respect to all 28 sensor pairings. This maintains the relative structure between experiments (sensor pairs) in the combined data. More specifically, a global normalization of the outputs is essential to prevent meaningful differences (between tests) from being scaled out of the data.
$ N=100 $
training data for each sensor pair combination, sampled uniformly from each task. We then normalize inputs with respect to the longest edge, such that the plate’s length is unity. This scaling maintains approximately the same relative smoothness of the map in each direction, that is one length scale for both dimensions. Rather than normalize the response for each plate independently, it is z-score normalized with respect to all 28 sensor pairings. This maintains the relative structure between experiments (sensor pairs) in the combined data. More specifically, a global normalization of the outputs is essential to prevent meaningful differences (between tests) from being scaled out of the data.
2.3. Why multilevel?
In the context of this work, each map and sensor pair corresponds to a distinct but related environment: each referred to as an experiment, with an associated predictive task learned as a regression. These collected environments are visualized in Figure 4. If one learns these maps collectively, in a combined inference, the model should capture variations between each sensor pair. These relationships capture further insights from the experimental campaign, which emerge at the systems level.
3. Representing AE maps with Gaussian Processes Regression
GPs are used to represent each of these experiments since they offer a flexible tool for regression with natural mechanisms to encode engineering knowledge and domain expertise. First, we consider one task at a time (Section 4 extends the model to consider all experiments in a combined inference). The additive noise
![]() $ {\unicode{x025B}}_i $
is assumed to be normally distributed,
$ {\unicode{x025B}}_i $
is assumed to be normally distributed,
in practice,
![]() $ {\unicode{x025B}}_i $
will represent more than observation noise, since it captures the combined uncertainty of the
$ {\unicode{x025B}}_i $
will represent more than observation noise, since it captures the combined uncertainty of the
![]() $ \Delta $
ToA extraction, from the raw time series data. Still, as with previous work [Reference Jones, Rogers, Worden and Cross21, Reference Jones, Rogers, Worden and Cross22, Reference Jones, Rogers and Cross12, Reference Hensman, Mills, Pierce, Worden and Eaton6], we found this representation works well in practice. Rather than suggest a parametrization of
$ \Delta $
ToA extraction, from the raw time series data. Still, as with previous work [Reference Jones, Rogers, Worden and Cross21, Reference Jones, Rogers, Worden and Cross22, Reference Jones, Rogers and Cross12, Reference Hensman, Mills, Pierce, Worden and Eaton6], we found this representation works well in practice. Rather than suggest a parametrization of
![]() $ f $
we assume that it has a nonparametric GP prior distributionFootnote 2,
$ f $
we assume that it has a nonparametric GP prior distributionFootnote 2,
The prior over
![]() $ f $
is specified by its mean
$ f $
is specified by its mean
![]() $ {m}_f $
and covariance
$ {m}_f $
and covariance
![]() $ {k}_f $
functions, where
$ {k}_f $
functions, where
![]() $ \boldsymbol{\theta} $
is the set of collected hyperparameters. These hyperparameters are sampled from the higher level distribution
$ \boldsymbol{\theta} $
is the set of collected hyperparameters. These hyperparameters are sampled from the higher level distribution
![]() $ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
whose prior is parametrised by constants in
$ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
whose prior is parametrised by constants in
![]() $ \boldsymbol{\phi} $
. The mean and covariance of the prior offer natural mechanisms to encode knowledge of the expected functions given domain expertise, before any data are observed. The covariance determines the expected correlation between outputs—influencing process variance, and smoothness—while the mean represents the prior expectation of the structure of the functions. A function sample from the GP, denoted
$ \boldsymbol{\phi} $
. The mean and covariance of the prior offer natural mechanisms to encode knowledge of the expected functions given domain expertise, before any data are observed. The covariance determines the expected correlation between outputs—influencing process variance, and smoothness—while the mean represents the prior expectation of the structure of the functions. A function sample from the GP, denoted
![]() $ \mathbf{f} $
, is multivariate normal for any finite set of
$ \mathbf{f} $
, is multivariate normal for any finite set of
![]() $ N $
observations,
$ N $
observations,
Since the observation model is assumed Gaussian, we can avoid sampling
![]() $ \mathbf{f} $
entirely by combining the GP kernel
$ \mathbf{f} $
entirely by combining the GP kernel
![]() $ {\mathbf{K}}_{\mathbf{f}} $
with the additive noise vector
$ {\mathbf{K}}_{\mathbf{f}} $
with the additive noise vector
![]() $ \sigma $
, to describe the likelihood function,
$ \sigma $
, to describe the likelihood function,
Following [Reference Jones, Rogers, Worden and Cross21] we use a zero-mean and Matérn
![]() $ 3/2 $
kernel function
$ 3/2 $
kernel function
![]() $ {k}_f $
for the covariance function,
$ {k}_f $
for the covariance function,
 $$ {\mathbf{K}}_{\mathbf{f}}\left[i,j\right]={\alpha}^2\left(1+\frac{\sqrt{3}\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|}{l}\right)\exp \left(-\frac{\sqrt{3}\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|}{l}\right) $$
$$ {\mathbf{K}}_{\mathbf{f}}\left[i,j\right]={\alpha}^2\left(1+\frac{\sqrt{3}\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|}{l}\right)\exp \left(-\frac{\sqrt{3}\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|}{l}\right) $$
The zero-mean function is justified since the complex plate geometry prevents the specification of a parametrized mean. In the absence of this information, a zero mean is usually sufficient practice, since the GP alone is flexible enough to model arbitrary trends, given enough training data. Two hyperparameters are introduced via the kernel
![]() $ {k}_f $
(3.10) such that
$ {k}_f $
(3.10) such that
![]() $ \boldsymbol{\theta} =\left\{\alpha, l\right\} $
. The process variance
$ \boldsymbol{\theta} =\left\{\alpha, l\right\} $
. The process variance
![]() $ \alpha $
encodes the magnitude of function variations around the expected mean. The length scale
$ \alpha $
encodes the magnitude of function variations around the expected mean. The length scale
![]() $ l $
encodes how much influence a training observation has on its neighboring inputs, it represents the smoothness of the approximating family of functions.
$ l $
encodes how much influence a training observation has on its neighboring inputs, it represents the smoothness of the approximating family of functions.
3.1. Heteroscedastic noise
In the experiments, the scale of the additive noise
![]() $ {\sigma}_i $
is expected to increase at the extremities of the plate [Reference Jones, Rogers, Worden and Cross22]. As such, the magnitude of the noise is input-dependent, and it is not statistically identical over the whole input (that is it is not homoscedastic). Such input-dependent noise can be represented with a heteroscedastic regression. Heteroscedasticity is implemented with another GP in a combined model, mapping the inputs
$ {\sigma}_i $
is expected to increase at the extremities of the plate [Reference Jones, Rogers, Worden and Cross22]. As such, the magnitude of the noise is input-dependent, and it is not statistically identical over the whole input (that is it is not homoscedastic). Such input-dependent noise can be represented with a heteroscedastic regression. Heteroscedasticity is implemented with another GP in a combined model, mapping the inputs
![]() $ {\mathbf{x}}_i $
to the scale of the additive noise
$ {\mathbf{x}}_i $
to the scale of the additive noise
![]() $ {\sigma}_i $
. This introduces the noise process
$ {\sigma}_i $
. This introduces the noise process
![]() $ r $
, where the prior utilizes a constant mean functionFootnote 3
$ r $
, where the prior utilizes a constant mean functionFootnote 3
![]() $ {m}_r\left({\mathbf{x}}_i\right)={m}_r $
and another Matérn
$ {m}_r\left({\mathbf{x}}_i\right)={m}_r $
and another Matérn
![]() $ 3/2 $
kernel function (with its own hyperparameters). Therefore, a finite sample from the noise process is distributed as follows,
$ 3/2 $
kernel function (with its own hyperparameters). Therefore, a finite sample from the noise process is distributed as follows,
 $$ {\displaystyle \begin{array}{c}{\mathbf{m}}_{\mathbf{r}}\left[i\right]={m}_r\\ {}{\mathbf{K}}_{\mathbf{r}}\left[i,j\right]={\alpha}_r^2\left(1+\frac{\sqrt{3}\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|}{l_r}\right)\exp \left(-\frac{\sqrt{3}\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|}{l_r}\right)\end{array}} $$
$$ {\displaystyle \begin{array}{c}{\mathbf{m}}_{\mathbf{r}}\left[i\right]={m}_r\\ {}{\mathbf{K}}_{\mathbf{r}}\left[i,j\right]={\alpha}_r^2\left(1+\frac{\sqrt{3}\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|}{l_r}\right)\exp \left(-\frac{\sqrt{3}\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|}{l_r}\right)\end{array}} $$
Samples from
![]() $ r $
are exponentiated to define
$ r $
are exponentiated to define
![]() $ \boldsymbol{\sigma} $
since the noise variance must be strictly positive (note that, untransformed, a GP will map to any real number). The exponential transformation requires a constant mean function, otherwise, the prior of the expected noise variance is too large, as a zero mean function would lead to
$ \boldsymbol{\sigma} $
since the noise variance must be strictly positive (note that, untransformed, a GP will map to any real number). The exponential transformation requires a constant mean function, otherwise, the prior of the expected noise variance is too large, as a zero mean function would lead to
![]() $ \exp (0)=1 $
. The additional hyperparameters from the noise process are now included in the total set
$ \exp (0)=1 $
. The additional hyperparameters from the noise process are now included in the total set
![]() $ \boldsymbol{\theta} $
,
$ \boldsymbol{\theta} $
,
3.2. Prior formulations
One should encode prior knowledge of the AE maps as prior distributions over the higher-level variables
![]() $ \boldsymbol{\theta} \sim p\left(\boldsymbol{\phi} \right) $
. The hyperparameters of the GP are sampled from these distributions, which characterize the expected variation, smoothness, and noise of the response. The following
$ \boldsymbol{\theta} \sim p\left(\boldsymbol{\phi} \right) $
. The hyperparameters of the GP are sampled from these distributions, which characterize the expected variation, smoothness, and noise of the response. The following
![]() $ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
structure is adopted,
$ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
structure is adopted,
where
![]() $ \mathrm{Gamma} $
and
$ \mathrm{Gamma} $
and
![]() $ \mathrm{Half}\hbox{-} {\mathrm{Normal}}^{+} $
are the Gamma and positive Half-Normal probability distribution functions respectively. The Half-Normal distribution is centered at zero, with support for positive values only. The constants in (3.14)–(3.18) correspond to
$ \mathrm{Half}\hbox{-} {\mathrm{Normal}}^{+} $
are the Gamma and positive Half-Normal probability distribution functions respectively. The Half-Normal distribution is centered at zero, with support for positive values only. The constants in (3.14)–(3.18) correspond to
![]() $ \boldsymbol{\phi} $
, and they are specified given the combined normalized space as weakly informative prior distributions, explained below.
$ \boldsymbol{\phi} $
, and they are specified given the combined normalized space as weakly informative prior distributions, explained below.
Recall that the inputs are normalized between [0, 1] with respect to the longest side. We expect a smooth
![]() $ \Delta $
ToA map
$ \Delta $
ToA map
![]() $ (f) $
and noise process
$ (f) $
and noise process
![]() $ (r) $
, so the Gamma distributed length scales
$ (r) $
, so the Gamma distributed length scales
![]() $ l $
(3.14) and
$ l $
(3.14) and
![]() $ {l}_r $
(3.17) have their mode at
$ {l}_r $
(3.17) have their mode at
![]() $ 1=\left(\mathtt{shape}-1\right)/\mathtt{rate} $
[Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3]. The output is z-score normalized, so we expect the process variance
$ 1=\left(\mathtt{shape}-1\right)/\mathtt{rate} $
[Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3]. The output is z-score normalized, so we expect the process variance
![]() $ \alpha $
should be less than unity (shrunk further by outliers). This is reflected by a half-normal distribution with a unit scale, with an expected value
$ \alpha $
should be less than unity (shrunk further by outliers). This is reflected by a half-normal distribution with a unit scale, with an expected value
![]() $ E\left[\alpha \right]=\frac{1\sqrt{2}}{\sqrt{\pi }}=0.8 $
.
$ E\left[\alpha \right]=\frac{1\sqrt{2}}{\sqrt{\pi }}=0.8 $
.
The expectation of the noise process
![]() $ r $
is set to
$ r $
is set to
![]() $ 0.08 $
, to encode prior belief of a signal-to-noise ratio of 10, in terms of expected scale,
$ 0.08 $
, to encode prior belief of a signal-to-noise ratio of 10, in terms of expected scale,
 $$ =\frac{1\sqrt{2}\times {\pi}^{-0.5}}{\exp \left(-2.5\right)}=\frac{0.8}{0.08} $$
$$ =\frac{1\sqrt{2}\times {\pi}^{-0.5}}{\exp \left(-2.5\right)}=\frac{0.8}{0.08} $$
A vague prior is defined as
![]() $ {\alpha}_r $
, which indicates high variance in the noise process
$ {\alpha}_r $
, which indicates high variance in the noise process
![]() $ r $
, to reflect weak a priori knowledge,
$ r $
, to reflect weak a priori knowledge,
 $$ \mathrm{E}\left[{\alpha}_r\right]=\frac{2\sqrt{2}}{\sqrt{\pi }}=1.6 $$
$$ \mathrm{E}\left[{\alpha}_r\right]=\frac{2\sqrt{2}}{\sqrt{\pi }}=1.6 $$
A high scale for the noise process is assumed, since it is known that measurement noise increases dramatically at the extremities of the plate, far from the centroid of sensor pairs [Reference Jones, Rogers, Worden and Cross22].
3.3. Inference and prediction
To identify the model and make predictions, one can infer the posterior distribution for latent variables
![]() $ p\left(\boldsymbol{\Theta} |\mathbf{y}\right) $
by conditioning the joint distribution (which encodes domain expertise via the model and the prior specification) on the training data
$ p\left(\boldsymbol{\Theta} |\mathbf{y}\right) $
by conditioning the joint distribution (which encodes domain expertise via the model and the prior specification) on the training data
![]() $ \mathbf{y} $
. We use
$ \mathbf{y} $
. We use
![]() $ \boldsymbol{\Theta} $
to generically collect all (unobservable) latent variables, including functions, parameters, and hyperparameters. The joint distribution is written as the product of two densities, referred to as the likelihood
$ \boldsymbol{\Theta} $
to generically collect all (unobservable) latent variables, including functions, parameters, and hyperparameters. The joint distribution is written as the product of two densities, referred to as the likelihood
![]() $ p\left(\mathbf{y}|\boldsymbol{\Theta} \right) $
(or the data distribution) and the prior
$ p\left(\mathbf{y}|\boldsymbol{\Theta} \right) $
(or the data distribution) and the prior
![]() $ p\left(\boldsymbol{\Theta} \right) $
,
$ p\left(\boldsymbol{\Theta} \right) $
,
During model design, we have specified the likelihood with (3.8) and the prior throughout (3.14)–(3.18). Applying the property of conditional probability to (3.22) we arrive at Baye’s rule and an expression for the posterior distribution,
While (3.23) is a straightforward application of conditioning [Reference Murphy4], in practice, the evaluation of the denominator (that is the marginal likelihood or evidence) is nontrivial. It is specified by the following integral, which is intractable for most prior-likelihood combinations,
The integral (3.24) is feasible for a subset of likelihood-prior distributions, known as conjugate pairs [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3]. In many practical applications, however, it becomes increasingly hard to justify the model and prior choices that lead to conjugacy. In our case, the prior formulation
![]() $ p\left(\boldsymbol{\theta} |\boldsymbol{\phi} \right) $
required for a multilevel representation leads to an intractable eq. (3.24).
$ p\left(\boldsymbol{\theta} |\boldsymbol{\phi} \right) $
required for a multilevel representation leads to an intractable eq. (3.24).
A number of approximate Bayesian methods are used with non-conjugate models. Here, we utilize a sampling-based solution, inferring the parameters using MCMC and the no U-turn implementation of Hamiltonian Monte Carlo [Reference Hoffman and Gelman23]. The models are implemented in the probabilistic programming language Stan [Reference Carpenter, Gelman, Hoffman, Lee, Goodrich, Betancourt, Brubaker, Guo, Li and Riddell24].
When predicting new (previously unobserved) data
![]() $ \tilde{\mathbf{y}} $
one (empirically) integrates out
$ \tilde{\mathbf{y}} $
one (empirically) integrates out
![]() $ \boldsymbol{\Theta} $
from the following product,
$ \boldsymbol{\Theta} $
from the following product,
For GP variables
![]() $ \left\{f,r\right\} $
, the distribution used to predict new inputs has an analytical solution when the hyperparameters
$ \left\{f,r\right\} $
, the distribution used to predict new inputs has an analytical solution when the hyperparameters
![]() $ \boldsymbol{\theta} $
are fixed. For the
$ \boldsymbol{\theta} $
are fixed. For the
![]() $ f $
-process, this would be
$ f $
-process, this would be
![]() $ p\left(\tilde{\mathbf{y}}|\mathbf{y},{\boldsymbol{\theta}}_s\right) $
where
$ p\left(\tilde{\mathbf{y}}|\mathbf{y},{\boldsymbol{\theta}}_s\right) $
where
![]() $ {\boldsymbol{\theta}}_s $
represents samples from the approximated posterior distribution. The analytical solution is then defined by conditioning a joint Gaussian, e.g.
$ {\boldsymbol{\theta}}_s $
represents samples from the approximated posterior distribution. The analytical solution is then defined by conditioning a joint Gaussian, e.g.
![]() $ p\left(\tilde{\mathbf{y}},\mathbf{y}|{\boldsymbol{\theta}}_s\right) $
, on the training variables for all samples from the approximated posterior distribution. The relevant identity is provided in Appendix A.
$ p\left(\tilde{\mathbf{y}},\mathbf{y}|{\boldsymbol{\theta}}_s\right) $
, on the training variables for all samples from the approximated posterior distribution. The relevant identity is provided in Appendix A.
For the (Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3,Reference Kreft and De Leeuw5) sensor pair, a random sample of N = 100 observations is used for training, and the rest are set aside as test data. Following inference and prediction, Figure 5 plots the mean of the posterior predictive distribution for the two-dimensional map over the plate. To visualize the predictive variance and its heteroscedastic nature, a random slice is taken along the length of the map and also plotted in Figure 5.

Figure 5. The inferred sensor pair (Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3,Reference Kreft and De Leeuw5) for the experiment k =15 (left) and a length-wise slice to visualize the heteroscedastic noise (right).
4. Multilevel representations
To conceptualize the hierarchical structure of the experimental data, independent GPs are learned for all 28 tests (rather than sensor pair (Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3, Reference Kreft and De Leeuw5) only). Recall that each pairwise map is distinguished with an index
![]() $ k\in \left\{1,2,\dots, 28\right\} $
listed in Table 2, Appendix B. The set of all maps is given by,
$ k\in \left\{1,2,\dots, 28\right\} $
listed in Table 2, Appendix B. The set of all maps is given by,
Throughout, we use the same test-train split of N = 100 random samples from each task, visualized in Figure 4. Figure 6 shows samples from the posterior distributions
![]() $ p\left(\boldsymbol{\theta} |{\mathbf{y}}_k\right)\forall k $
. Since the data are not shared between the experiments, each task is learned independently, and these models are considered single-task learners (STL) [Reference Murphy4]. Figure 6 is typical longitudinal or panel data [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3] where the task-specific
$ p\left(\boldsymbol{\theta} |{\mathbf{y}}_k\right)\forall k $
. Since the data are not shared between the experiments, each task is learned independently, and these models are considered single-task learners (STL) [Reference Murphy4]. Figure 6 is typical longitudinal or panel data [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3] where the task-specific
![]() $ \boldsymbol{\theta} $
are similar, with random variations. The experiment-specific models can be viewed as perturbations around an average (higher-level model). An intuitive concept, since all experiments concern the same plate, despite the varying experimental design (sensor placement).
$ \boldsymbol{\theta} $
are similar, with random variations. The experiment-specific models can be viewed as perturbations around an average (higher-level model). An intuitive concept, since all experiments concern the same plate, despite the varying experimental design (sensor placement).
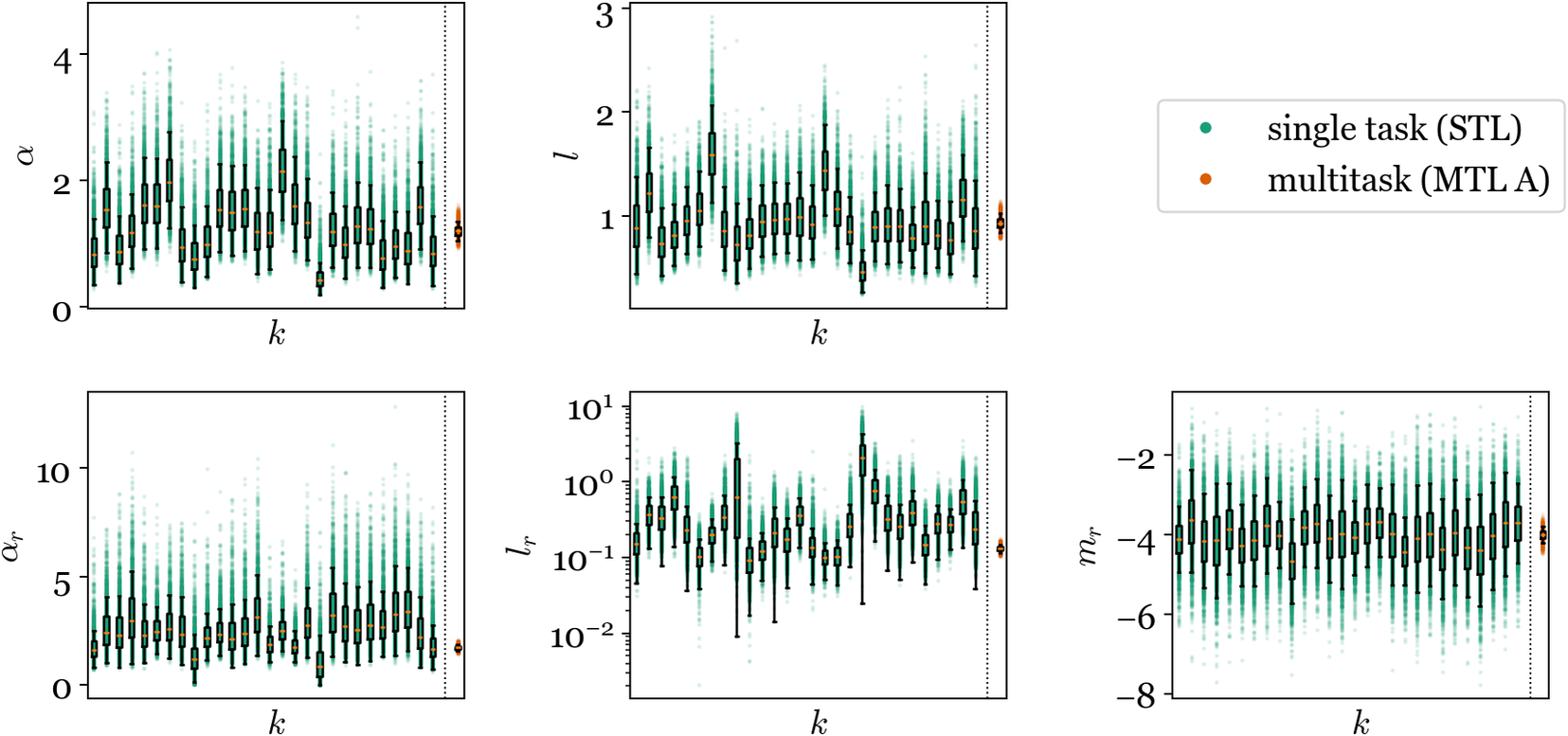
Figure 6. Posterior distribution of hyperparameters for independent GPs of each experiment (STL, green), compared to sharing hyperparameters (the prior) between all experiments (MTL-A, orange). Top row:
![]() $ f $
-process hyperparameters (AE map). Bottom row:
$ f $
-process hyperparameters (AE map). Bottom row:
![]() $ r $
-process hyperparameters (heteroscedastic noise).
$ r $
-process hyperparameters (heteroscedastic noise).
To summarize, each task represents a distinct but related environment. In turn, MTL is used to learn predictive maps in a combined inference, to capture the inter-task functions (with quantified uncertainty) relating to differences between tests in the experimental campaign.
4.1. (Method A) K GPs, one prior
In a combined inference, one simple way to share information between tests assumes that the smoothness
![]() $ l $
and process variance
$ l $
and process variance
![]() $ {\alpha}^2 $
of all
$ {\alpha}^2 $
of all
![]() $ \Delta $
ToA maps
$ \Delta $
ToA maps
![]() $ \left\{{f}_k\right\} $
are consistent. In other words, the GPs for each experiment are sampled from a shared prior,
$ \left\{{f}_k\right\} $
are consistent. In other words, the GPs for each experiment are sampled from a shared prior,
Same for the noise process
![]() $ {r}_k $
,
$ {r}_k $
,
Shared hyperparameters across all
![]() $ K $
GPs is one form of partial pooling [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3] and it will likely improve inference compared to independent learners. However, Figure 6 suggests the assumption of tied hyperparameters is too simple. Furthermore, process understanding supports this concern: it is unlikely that the independent posterior samples correspond to the same hyperparameter since there are differences in the design of each experiment. The question is whether the assumption provides a sufficient model. Considering the above, distinct maps for each experiment
$ K $
GPs is one form of partial pooling [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3] and it will likely improve inference compared to independent learners. However, Figure 6 suggests the assumption of tied hyperparameters is too simple. Furthermore, process understanding supports this concern: it is unlikely that the independent posterior samples correspond to the same hyperparameter since there are differences in the design of each experiment. The question is whether the assumption provides a sufficient model. Considering the above, distinct maps for each experiment
![]() $ \left\{{f}_k\right\} $
are sampled from GP priors with shared hyperparameters distributed by
$ \left\{{f}_k\right\} $
are sampled from GP priors with shared hyperparameters distributed by
![]() $ p\left(\boldsymbol{\theta} \right) $
. This approach is presented as a benchmark—multitask learning method A (MTL-A). The resultant hyperparameter posterior distributions are shown by orange markers in Figure 6. Their reduced variance is typical for pooled estimates because a single distribution is inferred from all
$ p\left(\boldsymbol{\theta} \right) $
. This approach is presented as a benchmark—multitask learning method A (MTL-A). The resultant hyperparameter posterior distributions are shown by orange markers in Figure 6. Their reduced variance is typical for pooled estimates because a single distribution is inferred from all
![]() $ K $
datasets (rather than one for each task). Caution is required, this assumption misrepresents the population variance if the model form is misspecified.
$ K $
datasets (rather than one for each task). Caution is required, this assumption misrepresents the population variance if the model form is misspecified.
4.2. (Method B) Hyperparameter modelling
A more intuitive generating process considers that certain hyperparameters are conditioned on the experimental setup, rather consistent, to better represent the differences between each test. We extend the notation of (3.2) with a
![]() $ k $
-index to reflect this,
$ k $
-index to reflect this,
 $$ {\displaystyle \begin{array}{l}{\boldsymbol{\theta}}_k\sim p\left(\boldsymbol{\phi} \right)\\ {}{\boldsymbol{\theta}}_k\hskip0.3em \triangleq \hskip0.4em \left\{{\alpha}_k,{l}_k\right\}\end{array}} $$
$$ {\displaystyle \begin{array}{l}{\boldsymbol{\theta}}_k\sim p\left(\boldsymbol{\phi} \right)\\ {}{\boldsymbol{\theta}}_k\hskip0.3em \triangleq \hskip0.4em \left\{{\alpha}_k,{l}_k\right\}\end{array}} $$
Distinct variables are considered for the
![]() $ {\mathbf{K}}_{\mathbf{f}} $
kernel only (
$ {\mathbf{K}}_{\mathbf{f}} $
kernel only (
![]() $ {\alpha}_k $
and
$ {\alpha}_k $
and
![]() $ {l}_k $
) since these are easier to interpret and relate to domain knowledge, especially if the plate had represented a simple geometry—this choice also helps to constrain the model design. Having a distinct set
$ {l}_k $
) since these are easier to interpret and relate to domain knowledge, especially if the plate had represented a simple geometry—this choice also helps to constrain the model design. Having a distinct set
![]() $ {\boldsymbol{\theta}}_k $
allows the characteristics of the map to vary between each experiment: this should be expected since they are different experimental designs. The higher-level sampling distribution
$ {\boldsymbol{\theta}}_k $
allows the characteristics of the map to vary between each experiment: this should be expected since they are different experimental designs. The higher-level sampling distribution
![]() $ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
remains shared between all experiments (and learned from pooled data to share information). We now consider modifications to the prior model
$ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
remains shared between all experiments (and learned from pooled data to share information). We now consider modifications to the prior model
![]() $ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
to encode knowledge and domain expertise of the intertask relationships, that is between the experiments.
$ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
to encode knowledge and domain expertise of the intertask relationships, that is between the experiments.
4.2.1. Beyond exchangeable experiments
When specifying a new prior model
![]() $ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
it is important to consider whether the experiments are exchangeable [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3]. Here, they would be considered exchangeable if no information is available to distinguish the
$ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
it is important to consider whether the experiments are exchangeable [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3]. Here, they would be considered exchangeable if no information is available to distinguish the
![]() $ {\boldsymbol{\theta}}_k $
‘s from one another. In other words, the set
$ {\boldsymbol{\theta}}_k $
‘s from one another. In other words, the set
![]() $ {\left\{{\boldsymbol{\theta}}_k\right\}}_{k=1}^k $
(presented in Figure 6) cannot be reordered such that patterns are revealed in the latent variables.
$ {\left\{{\boldsymbol{\theta}}_k\right\}}_{k=1}^k $
(presented in Figure 6) cannot be reordered such that patterns are revealed in the latent variables.
However, since we know about the design of the AE experiments, there are a few possibilities. One simple description is sensor separation, to order the models and reveal structure (that is patterns) in the hyperparameter estimates. Once structure appears, the experiments are no longer exchangeable. Sensor separation
![]() $ \delta {S}_k $
is defined as the Euclidean distance between any two of the eight
$ \delta {S}_k $
is defined as the Euclidean distance between any two of the eight
![]() $ \left(\begin{array}{c}8\\ {}2\end{array}\right) $
possible sensor locations
$ \left(\begin{array}{c}8\\ {}2\end{array}\right) $
possible sensor locations
![]() $ \hat{\mathbf{S}}=\left\{{\hat{\mathbf{s}}}_1,{\hat{\mathbf{s}}}_2,\dots {\hat{\mathbf{s}}}_8\right\} $
,
$ \hat{\mathbf{S}}=\left\{{\hat{\mathbf{s}}}_1,{\hat{\mathbf{s}}}_2,\dots {\hat{\mathbf{s}}}_8\right\} $
,
where the vector
![]() $ \delta \mathbf{S} $
will be length
$ \delta \mathbf{S} $
will be length
 $ K=\left(\begin{array}{c}8\\ {}2\end{array}\right)=28 $
. The values for sensor separation from each experiment are also presented in Table 2, Appendix B. The simple pattern we expect is that process variance
$ K=\left(\begin{array}{c}8\\ {}2\end{array}\right)=28 $
. The values for sensor separation from each experiment are also presented in Table 2, Appendix B. The simple pattern we expect is that process variance
![]() $ {\alpha}_k $
will be greater for sensors that are further apart; that is the variation in the
$ {\alpha}_k $
will be greater for sensors that are further apart; that is the variation in the
![]() $ \Delta $
ToA signal will be greater since the AE signals have the potential to travel further.
$ \Delta $
ToA signal will be greater since the AE signals have the potential to travel further.
Figure 7 plots the posterior distributions
![]() $ {\boldsymbol{\theta}}_k $
(STL) with respect to
$ {\boldsymbol{\theta}}_k $
(STL) with respect to
![]() $ \delta {S}_k $
for the independent models from Figure 6. These samples indicate parameter relationships that we hope to learn with the higher-level model
$ \delta {S}_k $
for the independent models from Figure 6. These samples indicate parameter relationships that we hope to learn with the higher-level model
![]() $ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
. (Note that in Figure 7, samples correspond to latent variables and not observations.)
$ p\left({\boldsymbol{\theta}}_k|\boldsymbol{\phi} \right) $
. (Note that in Figure 7, samples correspond to latent variables and not observations.)

Figure 7. Ordering the hyperparameters (conditional posterior distribution) from the STL experiments
![]() $ {\theta}_k $
with respect to sensor separation
$ {\theta}_k $
with respect to sensor separation
![]() $ \delta {S}_k $
. Black markers correspond to models of the hold-out tests
$ \delta {S}_k $
. Black markers correspond to models of the hold-out tests
![]() $ k\in \left\{\mathrm{4,7,16,22}\right\} $
which do not contribute training data for MTL.
$ k\in \left\{\mathrm{4,7,16,22}\right\} $
which do not contribute training data for MTL.
As expected, the process variance
![]() $ {\alpha}_k $
increases with sensor separation. The length scale
$ {\alpha}_k $
increases with sensor separation. The length scale
![]() $ {l}_k $
presents a similar trend: we believe the increasing length scale appears for smaller sensor spacing as the noise floor (observation noise as well as parameter uncertainty) is larger compared to the magnitude of the response variations (
$ {l}_k $
presents a similar trend: we believe the increasing length scale appears for smaller sensor spacing as the noise floor (observation noise as well as parameter uncertainty) is larger compared to the magnitude of the response variations (
![]() $ {\alpha}_k $
). In turn, the influence of each training observation on its neighbors is reduced.
$ {\alpha}_k $
). In turn, the influence of each training observation on its neighbors is reduced.
Figure 7 also highlights the hold-out experiments
![]() $ k\in \left\{\mathrm{4,7,16,22}\right\} $
represented by black markers (rather than green). Herein, hold-out experiments are not used when training (as with held-out data) to test interpolation and extrapolation in the hyperparameter space for the multilevel models.
$ k\in \left\{\mathrm{4,7,16,22}\right\} $
represented by black markers (rather than green). Herein, hold-out experiments are not used when training (as with held-out data) to test interpolation and extrapolation in the hyperparameter space for the multilevel models.
4.2.2. Intertask GPs
Like the input-dependent noise process (
![]() $ r $
) the variation of the hyperparameters (of
$ r $
) the variation of the hyperparameters (of
![]() $ {\mathbf{K}}_{\mathbf{f}} $
) can be represented with another function. The output of these functions is task-dependent (that is experiment-dependent). That is, the hyperparameters of the AE map
$ {\mathbf{K}}_{\mathbf{f}} $
) can be represented with another function. The output of these functions is task-dependent (that is experiment-dependent). That is, the hyperparameters of the AE map
![]() $ f $
are sampled from higher-level functions, denoted
$ f $
are sampled from higher-level functions, denoted
![]() $ \left\{g,h\right\} $
,
$ \left\{g,h\right\} $
,
where hyperparameter functions vary (between tasks) with respect to sensor separation
![]() $ \delta {S}_k $
for the 24 training experiments,
$ \delta {S}_k $
for the 24 training experiments,
Each GP is transformed to be strictly positive, as the hyperparameters they predict must be greater than zero. While the exponential function was used for this purpose with the noise process
![]() $ r $
(3.12) here softplus transformation [Reference Wiemann, Kneib and Hambuckers25] is used since it can be specified to approximate the identity function (
$ r $
(3.12) here softplus transformation [Reference Wiemann, Kneib and Hambuckers25] is used since it can be specified to approximate the identity function (
![]() $ \hskip0.1em f(a)=a\hskip0.1em $
) over the inputs of interest, aiding the interpretability of the hyperparameter models
$ \hskip0.1em f(a)=a\hskip0.1em $
) over the inputs of interest, aiding the interpretability of the hyperparameter models
![]() $ \left\{g,h\right\} $
. The exponentiated transformation is maintained for the lower-level GPs
$ \left\{g,h\right\} $
. The exponentiated transformation is maintained for the lower-level GPs
![]() $ {f}_k $
since it prevented divergences during inference via HMC, and aided convergence of the MCMC chains.
$ {f}_k $
since it prevented divergences during inference via HMC, and aided convergence of the MCMC chains.
4.2.3. Priors
The noise process prior distributions are set as before (3.16)–(3.18) while the AE map priors are sampled from GPs (4.7)–(4.9) whose hyperparameters are added to
![]() $ \theta $
. We use the same Matérn 3/2 kernel for the higher-level GPs (
$ \theta $
. We use the same Matérn 3/2 kernel for the higher-level GPs (
![]() $ {k}_g $
and
$ {k}_g $
and
![]() $ {k}_h $
); however, we use a linear mean function (with slope
$ {k}_h $
); however, we use a linear mean function (with slope
![]() $ \beta $
and gradient
$ \beta $
and gradient
![]() $ \gamma $
),
$ \gamma $
),
 $$ {\displaystyle \begin{array}{c}{\mathbf{K}}_{\mathbf{g}}\left[k,l\right]\hskip0.3em \triangleq \hskip0.3em {k}_g\left(\delta {S}_k,\delta {S}_l;\boldsymbol{\theta} \right)\\ {}{\mathbf{K}}_{\mathbf{h}}\left[k,l\right]\hskip0.3em \triangleq \hskip0.3em {k}_h\left(\delta {S}_k,\delta {S}_l;\boldsymbol{\theta} \right)\\ {}{\mathbf{m}}_{\mathbf{g}}\left[k\right]\hskip0.3em \triangleq \hskip0.3em {\beta}_g\delta {S}_k+{\gamma}_g\\ {}{\mathbf{m}}_{\mathbf{h}}\left[k\right]\hskip0.3em \triangleq \hskip0.3em {\beta}_h\delta {S}_k+{\gamma}_h\end{array}} $$
$$ {\displaystyle \begin{array}{c}{\mathbf{K}}_{\mathbf{g}}\left[k,l\right]\hskip0.3em \triangleq \hskip0.3em {k}_g\left(\delta {S}_k,\delta {S}_l;\boldsymbol{\theta} \right)\\ {}{\mathbf{K}}_{\mathbf{h}}\left[k,l\right]\hskip0.3em \triangleq \hskip0.3em {k}_h\left(\delta {S}_k,\delta {S}_l;\boldsymbol{\theta} \right)\\ {}{\mathbf{m}}_{\mathbf{g}}\left[k\right]\hskip0.3em \triangleq \hskip0.3em {\beta}_g\delta {S}_k+{\gamma}_g\\ {}{\mathbf{m}}_{\mathbf{h}}\left[k\right]\hskip0.3em \triangleq \hskip0.3em {\beta}_h\delta {S}_k+{\gamma}_h\end{array}} $$
The linear mean allows us to encode domain knowledge of a positive gradient (as a soft constraint) for the expected intertask functions via the GP prior. The conditional posterior predictive distributions of
![]() $ \left\{g,h\right\} $
then provide intertask relationships learned from the collected data (while only observing data as inputs on the lowest level
$ \left\{g,h\right\} $
then provide intertask relationships learned from the collected data (while only observing data as inputs on the lowest level
![]() $ f $
). The additional hyperparameters for the shared (global) sampling distributions are,
$ f $
). The additional hyperparameters for the shared (global) sampling distributions are,
![]() $ \left\{{\alpha}_g,{l}_g,{\alpha}_h,{l}_h,{\beta}_g,{\gamma}_g,{\beta}_h,{\gamma}_h\right\}\in \boldsymbol{\theta} $
where
$ \left\{{\alpha}_g,{l}_g,{\alpha}_h,{l}_h,{\beta}_g,{\gamma}_g,{\beta}_h,{\gamma}_h\right\}\in \boldsymbol{\theta} $
where
![]() $ \beta $
and
$ \beta $
and
![]() $ \gamma $
are the slope and intercepts of the linear mean function for the intertask relationships. The priors for each of these should reflect the difficulty in making specific statements around hyperparameter values, due to their limited interpretability,
$ \gamma $
are the slope and intercepts of the linear mean function for the intertask relationships. The priors for each of these should reflect the difficulty in making specific statements around hyperparameter values, due to their limited interpretability,
Given the normalized space, these priors encode weak knowledge and constrain the mean function to positive gradients. The upper bound (Reference Wahlström, Kok, Schön and Gustafsson10) of the uniform distribution was set to avoid divergences of the HMC samples and ensure convergence of MCMC. The descriptive multilevel model, with GPs representing hyperparameter variations, is referred to as multitask learning method B (MTL-B).
4.3. MTL comparison
Table 1 is provided to compare the parameter hierarchies between each method:
-
• Independent learners (STL)
-
• Shared GP prior (MTL-A)
-
• Hyperparameter modeling (MTL-B)
Table 1. Comparison of methods based on the hierarchy of latent variables

STL has distinct GPs
![]() $ \left\{f,r\right\} $
and associated hyperparameters
$ \left\{f,r\right\} $
and associated hyperparameters
![]() $ \left\{\alpha, l,{m}_r,{\alpha}_r,{l}_r\right\} $
for each task. MTL-A has distinct task GPs
$ \left\{\alpha, l,{m}_r,{\alpha}_r,{l}_r\right\} $
for each task. MTL-A has distinct task GPs
![]() $ \left\{f,r\right\} $
but shares hyperparameters
$ \left\{f,r\right\} $
but shares hyperparameters
![]() $ \left\{\alpha, l,{m}_r,{\alpha}_r,{l}_r\right\} $
between all tasks. Lastly, MTL-B has distinct GPs
$ \left\{\alpha, l,{m}_r,{\alpha}_r,{l}_r\right\} $
between all tasks. Lastly, MTL-B has distinct GPs
![]() $ \left\{f,r\right\} $
and hyperparameters of the response
$ \left\{f,r\right\} $
and hyperparameters of the response
![]() $ \left\{\alpha, l\right\} $
which are themselves predicted by intertask GPs
$ \left\{\alpha, l\right\} $
which are themselves predicted by intertask GPs
![]() $ \left\{g,h\right\} $
, with (shared) hyperparameters
$ \left\{g,h\right\} $
, with (shared) hyperparameters
![]() $ \left\{{\alpha}_g,{l}_g,{\alpha}_h,{l}_h\right\} $
.
$ \left\{{\alpha}_g,{l}_g,{\alpha}_h,{l}_h\right\} $
.
For visual comparison, Figure 8 plots the resultant hyperparameter posterior distributions for STL (green), MTL-A (orange), and MTL-B (purple). The (purple) functions
![]() $ \left\{g,h\right\} $
appear to capture the hyperparameter relationships, compared to the trends presented by the posterior distributions of the STL models. The variance of the functions is also reduced, compared to independent models (green), without the assumption of one consistent hyperparameter (orange). Critically, while each hyperparameter model makes sense given their respective assumptions, the GP model (purple) is more expressive: it represents the variations of the map between experiments with respect to an explanatory variable (sensor separation).
$ \left\{g,h\right\} $
appear to capture the hyperparameter relationships, compared to the trends presented by the posterior distributions of the STL models. The variance of the functions is also reduced, compared to independent models (green), without the assumption of one consistent hyperparameter (orange). Critically, while each hyperparameter model makes sense given their respective assumptions, the GP model (purple) is more expressive: it represents the variations of the map between experiments with respect to an explanatory variable (sensor separation).

Figure 8. Posterior distributions
![]() $ p\left({\boldsymbol{\theta}}_k|\mathbf{y}\right) $
following each method of learning from the series of AE experiments. Independent learners (STL, green); Shared GP prior (MTL-A, orange); Hyperparameter modeling (MTL-B, purple). Black markers correspond to STL models of the hold-out tests
$ p\left({\boldsymbol{\theta}}_k|\mathbf{y}\right) $
following each method of learning from the series of AE experiments. Independent learners (STL, green); Shared GP prior (MTL-A, orange); Hyperparameter modeling (MTL-B, purple). Black markers correspond to STL models of the hold-out tests
![]() $ k\in \left\{\mathrm{4,7,16,22}\right\} $
which do not contribute training data for MTL.
$ k\in \left\{\mathrm{4,7,16,22}\right\} $
which do not contribute training data for MTL.
To summarize, both the process variance
![]() $ {\alpha}_k $
and length scale
$ {\alpha}_k $
and length scale
![]() $ {l}_k $
increase with sensor separation
$ {l}_k $
increase with sensor separation
![]() $ \delta S $
. For process variance
$ \delta S $
. For process variance
![]() $ {\alpha}_k $
, this is because variation in the difference in time of arrival will be greater for sensors that are further apart. For the length scale
$ {\alpha}_k $
, this is because variation in the difference in time of arrival will be greater for sensors that are further apart. For the length scale
![]() $ {l}_k $
, we believe lower amplitude signals have a lower signal-to-noise ratio, therefore the inferred functions are less smooth (that is lower length scale).
$ {l}_k $
, we believe lower amplitude signals have a lower signal-to-noise ratio, therefore the inferred functions are less smooth (that is lower length scale).
4.3.1. Modelling hyperparameters, not parameters
Why not include
![]() $ \delta {S}_k $
as an explanatory variable on the lower level—within a product kernel, for example? This is because changes in the response are not smooth with respect to
$ \delta {S}_k $
as an explanatory variable on the lower level—within a product kernel, for example? This is because changes in the response are not smooth with respect to
![]() $ \delta {S}_k $
. Instead, the response surface switches discontinuously between experiments, see Figure 4. However, the response characteristics (smoothness, process variance) show smooth relationships with respect to
$ \delta {S}_k $
. Instead, the response surface switches discontinuously between experiments, see Figure 4. However, the response characteristics (smoothness, process variance) show smooth relationships with respect to
![]() $ \delta {S}_k $
(observed in Figures 7 and 8). For this reason, it is more appropriate to model variations at the hyperparameter level, rather than the map itself. The expected smoothness of intertask functions should be a primary consideration when building multilevel models.
$ \delta {S}_k $
(observed in Figures 7 and 8). For this reason, it is more appropriate to model variations at the hyperparameter level, rather than the map itself. The expected smoothness of intertask functions should be a primary consideration when building multilevel models.
4.3.2. Post-selection inference
By investigating (independent) model behavior with plots of the posterior distributions, we use the training data twice: (i) for inference and (ii) to inform model design. Specifically, Figure 7 was used to inform the structure of the multilevel model, so we are guilty of post-selection inference [Reference Lee, Sun, Sun and Taylor26]. With reference to Gelman et al. [Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin3], when the number of candidate models is small, the bias resulting from data reuse is also small. In this case study, the plots informed only certain aspects of the higher-level GP design. Post-selection inference should be treated cautiously, however, as when the number of candidate models grows, the risk of overfitting the data increases.
5. Results and discussion
To test each method of representing the experimental data, the ground truth (or target) out-of-sample data
![]() $ {\left\{{\overline{\mathbf{y}}}_k\right\}}_{k=1}^k $
are compared to the posterior predictive distribution. The predictive log-likelihood is used as a probabilistic assessment of performance,
$ {\left\{{\overline{\mathbf{y}}}_k\right\}}_{k=1}^k $
are compared to the posterior predictive distribution. The predictive log-likelihood is used as a probabilistic assessment of performance,
 $$ {lpY}_k=\sum \limits_{i=1}^N\log \left(\frac{1}{S}\sum \limits_{s=1}^Sp\left({\overline{y}}_{ik}|{\boldsymbol{\Theta}}_s\right)\right) $$
$$ {lpY}_k=\sum \limits_{i=1}^N\log \left(\frac{1}{S}\sum \limits_{s=1}^Sp\left({\overline{y}}_{ik}|{\boldsymbol{\Theta}}_s\right)\right) $$
where
![]() $ {\left\{{\boldsymbol{\Theta}}_s\right\}}_{s=1}^S $
are the
$ {\left\{{\boldsymbol{\Theta}}_s\right\}}_{s=1}^S $
are the
![]() $ S $
samples from the full approximated posterior distribution and the combined likelihood of all models is
$ S $
samples from the full approximated posterior distribution and the combined likelihood of all models is
![]() $ lpY={\sum}_{k=1}^K{lpY}_k $
. In other words, (5.1) quantifies the (log) likelihood that test data were generated by the model inferred from the training data. A higher value indicates that the model has a better approximation of the underlying data-generating process and indicates good generalization.
$ lpY={\sum}_{k=1}^K{lpY}_k $
. In other words, (5.1) quantifies the (log) likelihood that test data were generated by the model inferred from the training data. A higher value indicates that the model has a better approximation of the underlying data-generating process and indicates good generalization.
Figure 9 presents
![]() $ lpY $
for all benchmarks. There is a small improvement in the combined predictive likelihood for both MTL methods. Rather than motivate MTL, the predictive likelihoods show that hierarchical GPs maintain the predictive performance of the STL models. Insights are enabled in Figure 8, where the inferred intertask functions are presented with uncertainty quantification—e.g. these are used later for transfer learning in Section 5.1. For task-specific performance (
$ lpY $
for all benchmarks. There is a small improvement in the combined predictive likelihood for both MTL methods. Rather than motivate MTL, the predictive likelihoods show that hierarchical GPs maintain the predictive performance of the STL models. Insights are enabled in Figure 8, where the inferred intertask functions are presented with uncertainty quantification—e.g. these are used later for transfer learning in Section 5.1. For task-specific performance (
![]() $ {lpY}_k $
) independent STL performs better for a subset of tasks
$ {lpY}_k $
) independent STL performs better for a subset of tasks
![]() $ k\in \left\{\mathrm{3,8,10,11,13}\right\} $
. This is typical, however, since MTL considers the joint distribution of the whole data. If some experiments have data with fewer outliers and less noise, these might be negatively impacted by experiments with higher noise and sparse data. For example, in tasks with low sensor separation, the signal-to-noise ratio is lower, which might represent weak data.
$ k\in \left\{\mathrm{3,8,10,11,13}\right\} $
. This is typical, however, since MTL considers the joint distribution of the whole data. If some experiments have data with fewer outliers and less noise, these might be negatively impacted by experiments with higher noise and sparse data. For example, in tasks with low sensor separation, the signal-to-noise ratio is lower, which might represent weak data.

Figure 9. Predictive log-likelihood for the out-of-sample test data. Excluding hold-out experiments
![]() $ k\in \left\{\mathrm{4,7,16,22}\right\} $
which are modeled using transfer learning in s:transfer. Lines plot the average across all tasks, the combined log-likelihood (summed) for each method is: (STL, 84217), (MTL A, 85149), and (MTL B, 85204).
$ k\in \left\{\mathrm{4,7,16,22}\right\} $
which are modeled using transfer learning in s:transfer. Lines plot the average across all tasks, the combined log-likelihood (summed) for each method is: (STL, 84217), (MTL A, 85149), and (MTL B, 85204).
Both MTL-A and B extend data for training by partial pooling, but B has a more descriptive multilevel structure, allowing us to encode domain expertise for intertask (between experiment) learning. In turn, hyperparameter relationships are captured over the experimental campaign (rather than their marginal distribution). Modeling prior variations in MTL-B represents changes in the tasks with respect to experimental design parameters (in this case
![]() $ \delta {S}_k $
). To summarise:
$ \delta {S}_k $
). To summarise:
-
• (A & B) can simulate the hyperparameters for hypothetical/unobserved experimental setups
-
• (B) has the potential to encode physics/domain expertise of behavior between sensor pairs (mean functions, constraints)
-
• (A & B) can use the intertask relationships, learned from similar experiments, to predict hyperparameters for tasks with sparse data (this can be viewed as a form of transfer learning)
5.1. Using the multilevel model for transfer learning
To demonstrate transfer learning, the intertask functions are used for meta-modeling, to interpolate and extrapolate in the model space. The results intend to show how multilevel models can capture overarching insights from the experimental campaign (at the systems level) as well as task-specific insights. The expected hyperparameter values
![]() $ E\left[{\boldsymbol{\theta}}_k\right] $
from MTL-A and B can be visualized in Figure 8 with the solid lines. These point estimates are used when conditioning on data from the hold-out testsFootnote 4. In turn, hyperparameter inference can be avoided for new (previously unobserved) experiments. Instead, we predict their value given the other, similar experiments: where MTL-A assumes one hyperparameter set for all tests, and MTL-B learns how these vary with respect to sensor separation. By predicting hyperparameters, informed by data-rich tasks, the predictive performance should be improved for new experiments with sparse data.
$ E\left[{\boldsymbol{\theta}}_k\right] $
from MTL-A and B can be visualized in Figure 8 with the solid lines. These point estimates are used when conditioning on data from the hold-out testsFootnote 4. In turn, hyperparameter inference can be avoided for new (previously unobserved) experiments. Instead, we predict their value given the other, similar experiments: where MTL-A assumes one hyperparameter set for all tests, and MTL-B learns how these vary with respect to sensor separation. By predicting hyperparameters, informed by data-rich tasks, the predictive performance should be improved for new experiments with sparse data.
The expected hyperparameter values are used to condition new GPs for an increasing training budget (N = 5 − 100) for the hold-out experiments. Figure 10 shows that both forms of MTL consistently improve the predictive performance, especially when extrapolating in the model space (
![]() $ \delta S=0.54 $
). These improvements are intuitive since the extrapolated parameters are associated with higher uncertainty for conventional STL (refer to Figure 8). Another (more natural) way to share information would be to retrain the MTL models and include held-out experiments while increasing the training data. We favor the method presented here for computational reasons, referring again to the footnote
$ \delta S=0.54 $
). These improvements are intuitive since the extrapolated parameters are associated with higher uncertainty for conventional STL (refer to Figure 8). Another (more natural) way to share information would be to retrain the MTL models and include held-out experiments while increasing the training data. We favor the method presented here for computational reasons, referring again to the footnote
![]() $ {}^4 $
.
$ {}^4 $
.

Figure 10. Predictive log-likelihood for an increasing training budget for the hold-out experiments
![]() $ k\in \left\{\mathrm{4,7,16,22}\right\} $
. Conventional single-task learning (STL) compared to multitask learning (MTL) which predicts hyperparameter values from similar experiments. Averaged for 100 repeats.
$ k\in \left\{\mathrm{4,7,16,22}\right\} $
. Conventional single-task learning (STL) compared to multitask learning (MTL) which predicts hyperparameter values from similar experiments. Averaged for 100 repeats.
These results demonstrate transfer learning since the information from the training experiments (source tasks) is used to improve prediction for held-out experiments (target tasks). However, both MTL-A and B provide (effectively) the same performance increase. This raises the question: is the more descriptive model for
![]() $ p\left(\boldsymbol{\theta} |\phi \right) $
worth it, given that A provides the same predictive performance? We argue that this depends on the purpose of the model. If the purpose is purely prediction, the assumptions of A will likely be sufficient (in engineering, however, prediction is rarely the only motivation). On the other hand, B more closely resembles our understanding and domain expertise of the experimental campaign: it provides more insights regarding variations of the AE map between each experiment. In future work, stronger constraints could be applied to the parameters of the model directly (rather than hyperparameters). This structure would allow the meta-model to simulate the response
$ p\left(\boldsymbol{\theta} |\phi \right) $
worth it, given that A provides the same predictive performance? We argue that this depends on the purpose of the model. If the purpose is purely prediction, the assumptions of A will likely be sufficient (in engineering, however, prediction is rarely the only motivation). On the other hand, B more closely resembles our understanding and domain expertise of the experimental campaign: it provides more insights regarding variations of the AE map between each experiment. In future work, stronger constraints could be applied to the parameters of the model directly (rather than hyperparameters). This structure would allow the meta-model to simulate the response
![]() $ {\mathbf{y}}_k $
of unobserved experiments directly, and the inter-task functions would have more influence on predictive performance. However, these constraints would be more restrictive and require more specific domain knowledge, which was not available for these experiments.
$ {\mathbf{y}}_k $
of unobserved experiments directly, and the inter-task functions would have more influence on predictive performance. However, these constraints would be more restrictive and require more specific domain knowledge, which was not available for these experiments.
6. Concluding remarks
In this work, we demonstrated how multilevel Gaussian Processes (GPs) can be used as meta-models to represent an experimental campaign for nondestructive testing (NDT). Two model formulations were used to represent a series of experiments concerning source localization with AE data for a complex plate geometry. While the same plate was used throughout the test campaign, the experimental design was varied (re. sensor placement). By learning all tasks in a joint inference, the representation captures how characteristics of the AE map (that is hyperparameters) vary between the experiments. The model can also share information between tasks, to extend the (effective) number of training data and their value. We presented the intertask relations and explained how they inform insights into systems-level behavior, allowing domain expertise to be encoded between experiments, relating to the effects of design variables on the outcome of each test. The intertask functions were used as meta-models to predict hyperparameter values of similar (previously unobserved) experiments and enhance inference in new tasks by transfer learning. Looking forward, more specific physics-based constraints could be encoded into multilevel representations (via the kernel function) to describe intertask variations with physics-based models, that is differential equations. Instead, this article encoded general domain expertise of the underlying process (via the GP mean function) such that data simulated from the model reflected our understanding of the environment and experiments.
Data availability statement
While the experimental data in this work are not currently available to share, the stan code is hosted on https://github.com/labull/EngineeringPatternRecognition.
Acknowledgments
LAB and MG acknowledge the support of the UK Engineering and Physical Sciences Research Council (EPSRC) through the ROSEHIPS project (Grant EP/W005816/1). AD is supported by Wave 1 of The UKRI Strategic Priorities Fund under the EPSRC Grant EP/T001569/1 and EPSRC Grant EP/W006022/1, particularly the Ecosystems of Digital Twins theme within those grants & The Alan Turing Institute. EJC and MRJ are supported by grant reference numbers EP/S001565/1 and EP/R004900/1.
Author contribution
Conceptualization: LAB, MG, and MRJ.; Formal analysis: LAB and MRJ; Funding acquisition: EJC, AD, and MG; Investigation: LAB and MRJ; Methodology: LAB, MRJ, and AD; Software: LAB; Supervision: EJC, AD, and MG; Validation: MRJ; Writing, original draft: LAB; Writing, review & editing: MRJ and AD.
Funding statement
The support of Keith Worden during the completion of this work is gratefully acknowledged. Thanks are offered to James Hensman, Mark Eaton, Robin Mills, and Gareth Pierce for their work in generating the data used throughout this paper. For the purposes of open access, the authors have applied a Creative Commons Attribution (CC BY) license to any Author Accepted Manuscript version arising.
Competing interest
None.
Ethical standard
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Appendix
A. A Gaussian identity for GP prediction
Let
![]() $ \mathbf{x} $
and
$ \mathbf{x} $
and
![]() $ \mathbf{y} $
be jointly distributed Gaussian random vectors [Reference Rasmussen and Williams27],
$ \mathbf{y} $
be jointly distributed Gaussian random vectors [Reference Rasmussen and Williams27],
 $$ \left[\begin{array}{l}\mathbf{x}\\ {}\mathbf{y}\end{array}\right]\sim N\left(\left[\begin{array}{l}{\mu}_x\\ {}{\mu}_y\end{array}\right],\left[\begin{array}{ll}A& C\\ {}{C}^{\top }& B\end{array}\right]\right)=N\left(\left[\begin{array}{l}{\mu}_x\\ {}{\mu}_y\end{array}\right],{\left[\begin{array}{ll}\tilde{A}& \tilde{C}\\ {}{\tilde{C}}^{\top }& \tilde{B}\end{array}\right]}^{-1}\right) $$
$$ \left[\begin{array}{l}\mathbf{x}\\ {}\mathbf{y}\end{array}\right]\sim N\left(\left[\begin{array}{l}{\mu}_x\\ {}{\mu}_y\end{array}\right],\left[\begin{array}{ll}A& C\\ {}{C}^{\top }& B\end{array}\right]\right)=N\left(\left[\begin{array}{l}{\mu}_x\\ {}{\mu}_y\end{array}\right],{\left[\begin{array}{ll}\tilde{A}& \tilde{C}\\ {}{\tilde{C}}^{\top }& \tilde{B}\end{array}\right]}^{-1}\right) $$
The conditional distribution of
![]() $ \mathbf{x} $
given
$ \mathbf{x} $
given
![]() $ \mathbf{y} $
is
$ \mathbf{y} $
is
This conditional is used in GP predictive equations, for a given/fixed set (that is sample) of hyperparameters. For further details, refer to Rasmussen et al. [Reference Rasmussen and Williams27].
B. Pair label indices
Table 2. Experiment indices
![]() $ k $
, sensor pairs, and their separation
$ k $
, sensor pairs, and their separation
![]() $ \delta S $
(Euclidean distance in normalized space)
$ \delta S $
(Euclidean distance in normalized space)
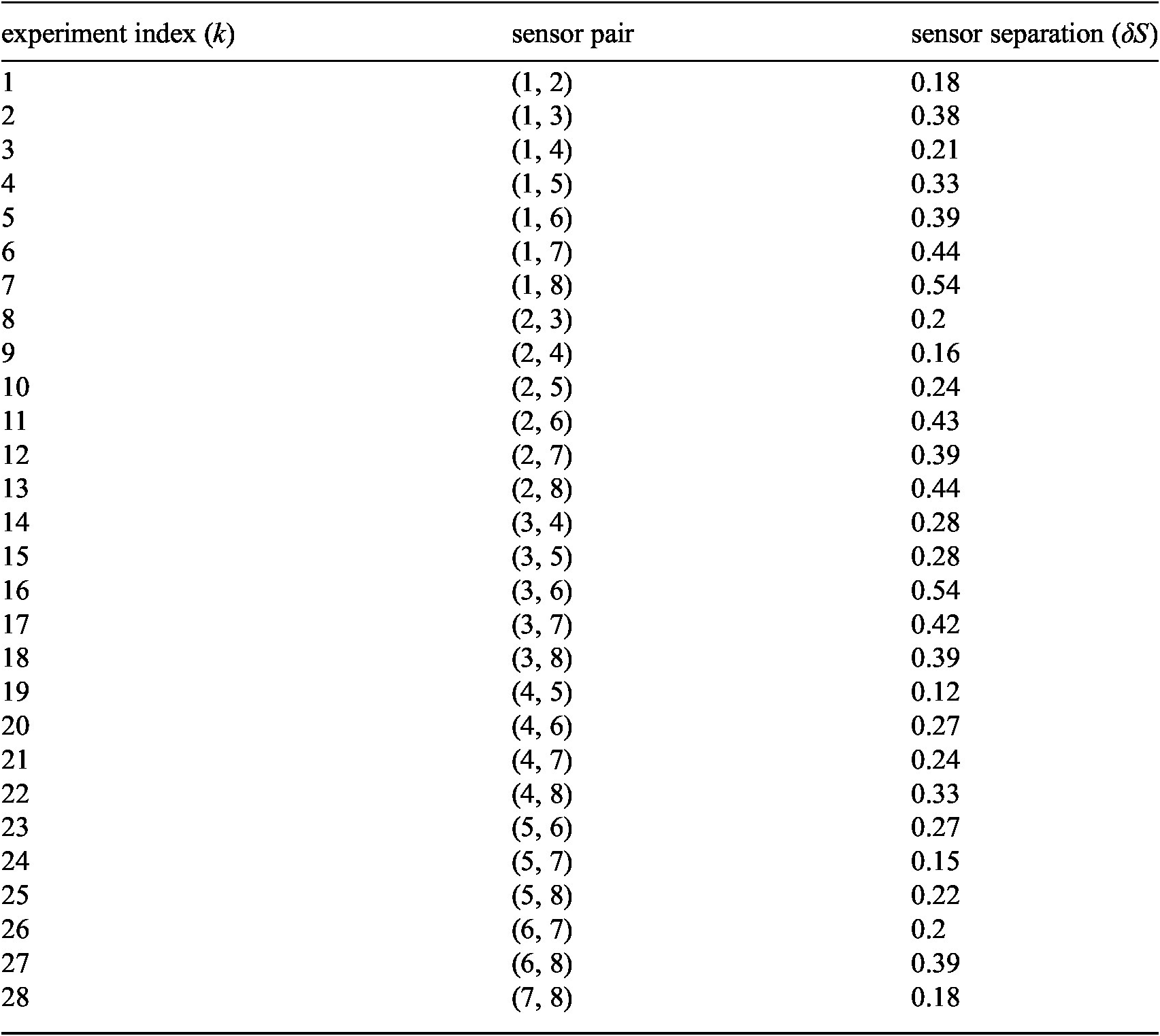













































Comments
No Comments have been published for this article.