We develop a dimension theory for coadmissible \widehat {\mathcal {D}}$\widehat {\mathcal {D}}$-modules on rigid analytic spaces and study those which are of minimal dimension, in analogy to the theory of holonomic \mathcal {D}$\mathcal {D}$-modules in the algebraic setting. We discuss a number of pathologies contained in this subcategory (modules of infinite length, infinite-dimensional fibres). We prove stability results for closed immersions and the duality functor, and show that all higher direct images of integrable connections restricted to a Zariski open subspace are coadmissible of minimal dimension. It follows that the local cohomology sheaves \underline {H}^{i}_Z(\mathcal {M})$\underline {H}^{i}_Z(\mathcal {M})$ with support in a closed analytic subset Z$Z$ of X$X$ are also coadmissible of minimal dimension for any integrable connection \mathcal {M}$\mathcal {M}$ on X$X$.

The aim of this paper is to establish exponential mixing of frame flows for convex cocompact hyperbolic manifolds of arbitrary dimension with respect to the Bowen–Margulis–Sullivan measure. Some immediate applications include an asymptotic formula for matrix coefficients with an exponential error term as well as the exponential equidistribution of holonomy of closed geodesics. The main technical result is a spectral bound on transfer operators twisted by holonomy, which we obtain by building on Dolgopyat's method.

Using the theory of 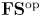{\mathbf {FS}} {^\mathrm {op}}${\mathbf {FS}} {^\mathrm {op}}$ modules, we study the asymptotic behavior of the homology of 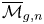{\overline {\mathcal {M}}_{g,n}}${\overline {\mathcal {M}}_{g,n}}$, the Deligne–Mumford compactification of the moduli space of curves, for 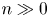n\gg 0$n\gg 0$. An 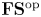{\mathbf {FS}} {^\mathrm {op}}${\mathbf {FS}} {^\mathrm {op}}$ module is a contravariant functor from the category of finite sets and surjections to vector spaces. Via copies that glue on marked projective lines, we give the homology of 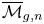{\overline {\mathcal {M}}_{g,n}}${\overline {\mathcal {M}}_{g,n}}$ the structure of an 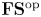{\mathbf {FS}} {^\mathrm {op}}${\mathbf {FS}} {^\mathrm {op}}$ module and bound its degree of generation. As a consequence, we prove that the generating function 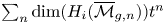\sum _{n} \dim (H_i({\overline {\mathcal {M}}_{g,n}})) t^n$\sum _{n} \dim (H_i({\overline {\mathcal {M}}_{g,n}})) t^n$ is rational, and its denominator has roots in the set 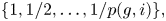\{1, 1/2, \ldots, 1/p(g,i)\},$\{1, 1/2, \ldots, 1/p(g,i)\},$ where 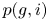p(g,i)$p(g,i)$ is a polynomial of order 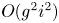O(g^2 i^2)$O(g^2 i^2)$. We also obtain restrictions on the decomposition of the homology of 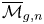{\overline {\mathcal {M}}_{g,n}}${\overline {\mathcal {M}}_{g,n}}$ into irreducible 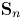\mathbf {S}_n$\mathbf {S}_n$ representations.

In the present article, we study the following problem. Let \boldsymbol {G}$\boldsymbol {G}$ be a linear algebraic group over \mathbb {Q}$\mathbb {Q}$, let \Gamma$\Gamma$ be an arithmetic lattice, and let \boldsymbol {H}$\boldsymbol {H}$ be an observable \mathbb {Q}$\mathbb {Q}$-subgroup. There is a H$H$-invariant measure \mu _H$\mu _H$ supported on the closed submanifold H\Gamma /\Gamma$H\Gamma /\Gamma$. Given a sequence (g_n)$(g_n)$ in G$G$, we study the limiting behavior of (g_n)_*\mu _H$(g_n)_*\mu _H$ under the weak-*$*$ topology. In the non-divergent case, we give a rather complete classification. We further supplement this by giving a criterion of non-divergence and prove non-divergence for arbitrary sequence (g_n)$(g_n)$ for certain large \boldsymbol {H}$\boldsymbol {H}$. We also discuss some examples and applications of our result. This work can be viewed as a natural extension of the work of Eskin–Mozes–Shah and Shapira–Zheng.

In quantum geometric Langlands, the Satake equivalence plays a less prominent role than in the classical theory. Gaitsgory and Lurie proposed a conjectural substitute, later termed the fundamental local equivalence. With a few exceptions, we prove this conjecture and its extension to the affine flag variety by using what amount to Soergel module techniques.

Let F$F$ be a non-archimedean local field of residual characteristic p \neq 2$p \neq 2$. Let G$G$ be a (connected) reductive group over F$F$ that splits over a tamely ramified field extension of F$F$. We revisit Yu's construction of smooth complex representations of G(F)$G(F)$ from a slightly different perspective and provide a proof that the resulting representations are supercuspidal. We also provide a counterexample to Proposition 14.1 and Theorem 14.2 in Yu [Construction of tame supercuspidal representations, J. Amer. Math. Soc. 14 (2001), 579–622], whose proofs relied on a typo in a reference.