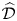Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T07:28:25.687Z Has data issue: false hasContentIssue false
  • English
  • Français

$\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations

Part of: Arithmetic problems. Diophantine geometry Analytic spaces

Published online by Cambridge University Press:  28 October 2021

Konstantin Ardakov ,
Andreas Bode  and
Simon Wadsley
Konstantin Ardakov
Affiliation:
Mathematical Institute, University of Oxford, OxfordOX2 6GG, [email protected]
Andreas Bode
Affiliation:
Unité de mathematiques pures et appliquées, École normale supérieure de Lyon, 46 allée d'Italie, 69364Lyon, [email protected]
Simon Wadsley
Affiliation:
Homerton College, CambridgeCB2 8PQ, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a dimension theory for coadmissible 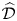$\widehat {\mathcal {D}}$-modules on rigid analytic spaces and study those which are of minimal dimension, in analogy to the theory of holonomic 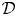$\mathcal {D}$-modules in the algebraic setting. We discuss a number of pathologies contained in this subcategory (modules of infinite length, infinite-dimensional fibres). We prove stability results for closed immersions and the duality functor, and show that all higher direct images of integrable connections restricted to a Zariski open subspace are coadmissible of minimal dimension. It follows that the local cohomology sheaves 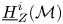$\underline {H}^{i}_Z(\mathcal {M})$ with support in a closed analytic subset 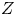$Z$ of 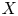$X$ are also coadmissible of minimal dimension for any integrable connection 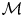$\mathcal {M}$ on 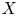$X$.

Keywords

${\mathcal {D}}$-modulesrigid analytic spacesholonomicitylocal cohomology

MSC classification

Primary: 14G22: Rigid analytic geometry 32C38: Sheaves of differential operators and their modules, $D$-modules
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 12 , December 2021 , pp. 2553 - 2584
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first and second authors acknowledge support from the EPSRC grant EP/L005190/1.

References

Atiyah, M. F. and Macdonald, I. G., Introduction to commutative algebra (Addison-Wesley, Reading, MA, 1969).Google Scholar
Ajitabh, K., Smith, S. P. and Zhang, J. J., Injective resolutions of some regular rings, J. Pure Appl. Algebra 140 (1999), 1–21.CrossRefGoogle Scholar
Ardakov, K. and Wadsley, S. J., On irreducible representations of compact $p$-adic analytic groups, Ann. of Math. (2) 178 (2013), 453–557.CrossRefGoogle Scholar
Ardakov, K. and Wadsley, S. J., $\widehat {\mathcal {D}}$-modules on rigid analytic spaces II: Kashiwara's equivalence, J. Algebraic Geom. 27 (2018), 647–701.CrossRefGoogle Scholar
Ardakov, K. and Wadsley, S. J., $\widehat {\mathcal {D}}$-modules on rigid analytic spaces I, J. Reine Angew. Math. 747 (2019), 221–275.CrossRefGoogle Scholar
Bitoun, T. and Bode, A., Extending meromorphic connections to coadmissible $\widehat {\mathcal {D}}$-modules, J. Reine Angew. Math. 778 (2021), 97–118.CrossRefGoogle Scholar
Bezrukavnikov, R., Braverman, A. and Positelskii, L., Gluing of abelian categories and differential operators on the basic affine space, J. Inst. Math. Jussieu 1 (2002), 543–557.CrossRefGoogle Scholar
Berthelot, P., $\mathcal {D}$-modules arithmétiques I. Opérateurs différentiels de niveau fini, Ann. Sci. Éc. Norm. Supér. (4) 29 (1996), 185–272.CrossRefGoogle Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean analysis, Grundlehren der Mathematischen Wissenschaften, vol. 261 (Springer, Berlin, 1984).CrossRefGoogle Scholar
Bjork, J.-E., The Auslander condition on Noetherian rings, in Séminaire d'Algèbre Paul Dubreil et Marie-Paul Malliavin, 39ème Année (Paris, 1987/1988), Lecture Notes in Mathematics, vol. 1404 (Springer, Berlin, 1989), 137–173.CrossRefGoogle Scholar
Berger, R., Kiehl, R., Kunz, E. and Nastold, H.-J., Differentialrechnung in der analytischen Geometrie, Lecture Notes in Mathematics, vol. 38 (Springer, Berlin, 1967).CrossRefGoogle Scholar
Bosch, S. and Lütkebohmert, W., Formal and rigid geometry. I. Rigid spaces, Math. Ann. 295 (1993), 291–317.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Formal and rigid geometry. III. The relative maximum principle, Math. Ann. 302 (1995), 1–29.CrossRefGoogle Scholar
Bode, A., Completed tensor products and a global approach to $p$-adic analytic differential operators, Math. Proc. Cambridge Philos. Soc. 167 (2019), 389–416.CrossRefGoogle Scholar
Bode, A., A Proper Mapping Theorem for coadmissible $\widehat {\mathcal {D}}$-modules, Münster J. Math. 12 (2019), 163–214.Google Scholar
Bosch, S., Lectures on formal and rigid geometry, Lecture Notes in Mathematics, vol. 2105 (Springer, Cham, 2014).Google Scholar
Caro, D., $\mathscr {D}$-modules arithmétiques surcohérents. Application aux fonction L, Ann. Inst. Fourier (Grenoble) 54 (2004), 1943–1996.CrossRefGoogle Scholar
Caro, D., $\mathscr {D}$-modules arithmétiques surholonomes, Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 141–192.CrossRefGoogle Scholar
Grothendieck, A., Élements de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. I., Publ. Math. Inst. Hautes Études Sci. 11 (1961), 349–511.Google Scholar
Hartl, U. T., Semi-stable models for rigid-analytic spaces, Manuscripta Math. 110 (2003), 365–380.CrossRefGoogle Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., $\mathscr {D}$-modules, perverse sheaves, and representation theory, Progress in Mathematics, vol. 236 (Birkhäuser, Boston, 2008).CrossRefGoogle Scholar
Iwanaga, Y., Duality over Auslander–Gorenstein rings, Math. Scand. 81 (1997), 184–190.CrossRefGoogle Scholar
Jans, J. P., Rings and homology (Holt, Rinehart and Winston, New York, 1964).Google Scholar
Kedlaya, K., $p$-adic differential equations, Cambridge Studies in Advanced Mathematics, vol. 125 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Kiehl, R., Theorem A und Theorem B in der nichtarchimedischen Funktionentheorie, Invent. Math. 2 (1967), 256–273.CrossRefGoogle Scholar
Kisin, M., Analytic functions on Zariski open sets, and local cohomology, J. Reine Angew. Math. 506 (1999), 117–144.CrossRefGoogle Scholar
Kopf, U., Über eigentliche Familien algebraischer Varietäten über affinoiden Räumen, Schriftenr. Math. Univ. Münster 2 (1974).Google Scholar
Kashiwara, M. and Schapira, P., Categories and sheaves, Grundlehren der Mathematischen Wissenschaften, vol. 332 (Springer, Berlin, 2006).CrossRefGoogle Scholar
Levasseur, T., Complexe bidualisant en algèbre non commutative, in Séminaire d'Algèbre Paul Dubreil et Marie-Paul Malliavin, 36ème Année (Paris, 1983–1984), Lecture Notes in Mathematics, vol. 1146 (Springer, Berlin, 1985), 270–287.Google Scholar
Levasseur, T., Some properties of noncommutative regular graded rings, Glasgow J. Math. 34 (1992), 277–300.CrossRefGoogle Scholar
Li, H., Lifting Ore sets of Noetherian filtered rings and applications, J. Algebra 179 (1996), 686–703.Google Scholar
Levasseur, T. and Stafford, J. T., Differential operators and cohomology groups on the basic affine space, in Studies in Lie theory, Progress in Mathematics, vol. 243 (Birkhäuser, Boston, 2006), 377–403.CrossRefGoogle Scholar
Liu, R. and Zhu, X., Rigidity and a Riemann–Hilbert correspondence for $p$-adic local systems, Invent. Math. 207 (2017), 291–343.CrossRefGoogle Scholar
Mebkhout, Z. and Narvaez-Macarro, L., La théorie du polynôme de Bernstein–Sato pour les algèbres de Tate et de Dwork–Monsky–Washnitzer, Ann. Sci. Éc. Norm. Supér. (4) 24 (1991), 227–256.CrossRefGoogle Scholar
Rinehart, G. S., Differential forms on general commutative algebras, Trans. Amer. Math. Soc. 108 (1963), 195–222.CrossRefGoogle Scholar
Schoutens, H., Embedded resolutions of singularities in rigid analytic geometry, Ann. Fac. Sci. Toulouse Math. (6) 8 (1999), 297–330.CrossRefGoogle Scholar
Schmidt, T. and Strauch, M., Dimensions of some locally analytic representations, Represent. Theory 20 (2016), 14–38.CrossRefGoogle Scholar
Schneider, P. and Teitelbaum, J., Algebras of $p$-distributions and admissible representations, Invent. Math. 153 (2003), 145–196.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks project (2018), http://stacks.columbia.edu.Google Scholar
Temkin, M., Functorial desingularization over $\mathbb {Q}$: boundaries and the embedded case, Israel J. Math. 224 (2018), 455–504.CrossRefGoogle Scholar
Watanabe, K., Ishikawa, T., Tachibana, S. and Otsuka, K., On tensor products of Gorenstein rings, J. Math. Kyoto Univ. 9 (1969), 413–423.Google Scholar