Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T01:50:53.244Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological complexity of collision-free motion planning on surfaces

Part of: Special aspects of infinite or finite groups Fiber spaces and bundles Classical Topics in Algebraic Topology

Published online by Cambridge University Press:  27 September 2010

Daniel C. Cohen  and
Michael Farber
Daniel C. Cohen
Affiliation:
Department of Mathematics, Louisiana State University, Baton Rouge, LA 70803, USA (email: [email protected])
Michael Farber
Affiliation:
Department of Mathematics, University of Durham, Durham DH1 3LE, UK (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The topological complexity 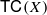is a numerical homotopy invariant of a topological space X which is motivated by robotics and is similar in spirit to the classical Lusternik–Schnirelmann category of X. Given a mechanical system with configuration space X, the invariant 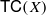measures the complexity of motion planning algorithms which can be designed for the system. In this paper, we compute the topological complexity of the configuration space of n distinct ordered points on an orientable surface, for both closed and punctured surfaces. Our main tool is a theorem of B. Totaro describing the cohomology of configuration spaces of algebraic varieties. For configuration spaces of punctured surfaces, this is used in conjunction with techniques from the theory of mixed Hodge structures.

Keywords

surface configuration spacetopological complexity

MSC classification

Secondary: 55R80: Discriminantal varieties, configuration spaces 20F36: Braid groups; Artin groups 55M30: Ljusternik-Schnirelman (Lyusternik-Shnirel'man) category of a space
Type
Research Article
Information
Compositio Mathematica , Volume 147 , Issue 2 , March 2011 , pp. 649 - 660
Copyright
Copyright © Foundation Compositio Mathematica 2010

References

[1]Aramova, A., Herzog, J. and Hibi, T., Gotzmann theorems for exterior algebras and combinatorics, J. Algebra 191 (1997), 174–211; MR 1444495.CrossRefGoogle Scholar
[2]Arnol’d, V. I., The cohomology ring of the group of dyed braids, Math. Notes 5 (1969), 138–140; MR 0242196.CrossRefGoogle Scholar
[3]Bellingeri, P., On presentations of surface braid groups, J. Algebra 274 (2004), 543–563; MR 2043362.CrossRefGoogle Scholar
[4]Cohen, F. R., The homology of 𝒞n+1-spaces, n≥0, in The homology of iterated loop spaces, Lecture Notes in Mathematics, vol. 533 (Springer, Berlin, 1976), 207–352; MR 0436146.CrossRefGoogle Scholar
[5]Cohen, D., Cohomology rings of almost-direct products of free groups, Compositio Math. 146 (2010), 465–479.CrossRefGoogle Scholar
[6]Cohen, D. and Suciu, A., Homology of iterated semidirect products of free groups, J. Pure Appl. Algebra 126 (1998), 87–120; MR 1600518.CrossRefGoogle Scholar
[7]Cohen, F. R. and Taylor, L., Computations of Gelfand–Fuks cohomology, the cohomology of function spaces, and the cohomology of configuration spaces, in Geometric applications of homotopy theory, I, Lecture Notes in Mathematics, vol. 657 (Springer, Berlin, 1978), 106–143; MR 0513543.CrossRefGoogle Scholar
[8]Dimca, A., Singularities and topology of hypersurfaces, Universitext (Springer, New York, 1992); MR 1194180.CrossRefGoogle Scholar
[9]Fadell, E. and Neuwirth, L., Configuration spaces, Math. Scand. 10 (1962), 119–126; MR 0141126.CrossRefGoogle Scholar
[10]Farber, M., Topological complexity of motion planning, Discrete Comput. Geom. 29 (2003), 211–221; MR 1957228.CrossRefGoogle Scholar
[11]Farber, M., Instabilities of robot motion, Topology Appl. 140 (2004), 245–266; MR 2074919.CrossRefGoogle Scholar
[12]Farber, M., Topology of robot motion planning, in Morse theoretic methods in non-linear analysis and in symplectic topology, NATO Science Series II: Mathematics, Physics and Chemistry, vol. 217 (Springer, Dordrecht, 2006), 185–230; MR 2276952.Google Scholar
[13]Farber, M., Invitation to topological robotics, Zurich Lectures in Advanced Mathematics (Eur. Math. Soc., Zürich, Switzerland, 2008); MR 2455573.CrossRefGoogle Scholar
[14]Farber, M. and Grant, M., Topological complexity of configuration spaces, Proc. Amer. Math. Soc. 137 (2009), 1841–1847; MR 2470845.CrossRefGoogle Scholar
[15]Farber, M., Grant, M. and Yuzvinsky, S., Topological complexity of collision free motion planning algorithms in the presence of multiple moving obstacles, in Topology and robotics, Contemporary Mathematics, vol. 438 (American Mathematical Society, Providence, RI, 2007), 75–83; MR 2359030.CrossRefGoogle Scholar
[16]Farber, M. and Yuzvinsky, S., Topological robotics: subspace arrangements and collision free motion planning, in Geometry, topology, and mathematical physics, American Mathematical Society Translations, Series 2, vol. 212 (American Mathematical Society, Providence, RI, 2004), 145–156; MR 2070052.Google Scholar
[17]Feichtner, E. and Ziegler, G., The integral cohomology algebras of ordered configuration spaces of spheres, Doc. Math. 5 (2000), 115–139; MR 1752611.CrossRefGoogle Scholar
[18]Gonçalves, D. and Guaschi, J., On the structure of surface pure braid groups, J. Pure Appl. Algebra 182 (2003), 33–64; MR 1977999.CrossRefGoogle Scholar
[19]Griffiths, P. and Schmid, W., Recent developments in Hodge theory: a discussion of techniques and results, in Discrete subgroups of Lie groups and applicatons to moduli (Oxford University Press, Bombay, 1975), 31–127; MR 0419850.Google Scholar
[20]James, I. M., On category, in the sense of Lusternik–Schnirelmann, Topology 17 (1978), 331–348; MR 0516214.CrossRefGoogle Scholar
[21]Latombe, J.-C., Robot motion planning (Kluwer, Dordrecht, 1991).CrossRefGoogle Scholar
[22]Milnor, J. and Stasheff, J., Characteristic classes, Annals of Mathematics Studies, vol. 76 (Princeton University Press, Princeton, NJ, 1974); (University of Tokyo Press, Tokyo, 1974); MR 0440554.CrossRefGoogle Scholar
[23]Peters, C. and Steenbrink, J., Mixed Hodge structures, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 52 (Springer, Berlin, 2008); MR 2393625.Google Scholar
[24]Schwarz, A., The genus of a fiber space, Amer. Math. Soc. Transl. 55 (1966), 49–140; MR 0154284.Google Scholar
[25]Sharir, M., Algorithmic motion planning, in Handbook of discrete and computational geometry, CRC Press Series on Discrete Mathematics and its Applications (CRC, Boca Raton, FL, 1997), 733–754; MR 1730196.Google Scholar
[26]Totaro, B, Configuration spaces of algebraic varieties, Topology 35 (1996), 1057–1067; MR 1404924.CrossRefGoogle Scholar
[27]Yuzvinsky, S., Orlik–Solomon algebras in algebra and topology, Russian Math. Surveys 56 (2001), 293–364; MR 1859708.CrossRefGoogle Scholar