Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-16T15:22:15.155Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular Gauduchon metrics

Part of: Families, fibrations Global differential geometry Analytic spaces

Published online by Cambridge University Press:  17 August 2022

Chung-Ming Pan
Chung-Ming Pan*
Affiliation:
Institut de Mathématiques de Toulouse, UMR 5219, Université de Toulouse, CNRS, UPS, 118 route de Narbonne, F-31062 Toulouse Cedex 9, France [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1977, Gauduchon proved that on every compact hermitian manifold 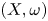$(X, \omega )$ there exists a conformally equivalent hermitian metric 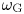$\omega _\mathrm {G}$ which satisfies 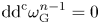$\mathrm {dd}^{\mathrm {c}} \omega _\mathrm {G}^{n-1} = 0$. In this note, we extend this result to irreducible compact singular hermitian varieties which admit a smoothing.

Keywords

Gauduchon metricscomplex spacessmoothable singularities

MSC classification

Primary: 53C55: Hermitian and Kählerian manifolds
Secondary: 14D06: Fibrations, degenerations 32C15: Complex spaces 53C15: General geometric structures on manifolds (almost complex, almost product structures, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 6 , June 2022 , pp. 1314 - 1328
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alessandrini, L. and Bassanelli, G., Plurisubharmonic currents and their extension across analytic subsets, Forum Math. 5 (1993), 577–602.CrossRefGoogle Scholar
Angella, D., Calamai, S. and Spotti, C., On the Chern-Yamabe problem, Math. Res. Lett. 24 (2017), 645–677.CrossRefGoogle Scholar
Berndtsson, B., $L^{2}$-extension of $\overline {\partial }$-closed form, Illinois J. Math. 56 (2012), 21–31 (2013).CrossRefGoogle Scholar
Campana, F., Guenancia, H. and Păun, M., Metrics with cone singularities along normal crossing divisors and holomorphic tensor fields, Ann. Sci. Éc. Norm. Supér. (4) 46 (2013), 879–916.CrossRefGoogle Scholar
Chuan, M.-T., Existence of Hermitian-Yang-Mills metrics under conifold transitions, Comm. Anal. Geom. 20 (2012), 677–749.CrossRefGoogle Scholar
Clemens, C. H., Double solids, Adv. Math. 47 (1983), 107–230.CrossRefGoogle Scholar
Collins, T. C., Picard, S. and Yau, S.-T., Stability of the tangent bundle through conifold transitions, Preprint (2021), arXiv:2102.11170.Google Scholar
Dabbek, K., Elkhadhra, F. and El Mir, H., Extension of plurisubharmonic currents, Math. Z. 245 (2003), 455–481.CrossRefGoogle Scholar
Demailly, J.-P., Mesures de Monge–Ampère et caractérisation géométrique des variétés algébriques affines, Mém. Soc. Math. Fr. (N.S.) 19 (1985), 124.Google Scholar
Di Nezza, E., Guedj, V. and Guenancia, H., Families of singular Kähler-Einstein metrics, J. Eur. Math. Soc., to appear. Preprint (2020), arXiv:2003.08178.Google Scholar
El Mir, H., Sur le prolongement des courants positifs fermés, Acta Math. 153 (1984), 1–45.CrossRefGoogle Scholar
Evans, L. C. and Gariepy, R. F., Measure theory and fine properties of functions, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1992).Google Scholar
Fino, A. and Ugarte, L., On generalized Gauduchon metrics, Proc. Edinb. Math. Soc. (2) 56 (2013), 733–753.CrossRefGoogle Scholar
Friedman, R., Simultaneous resolution of threefold double points, Math. Ann. 274 (1986), 671–689.CrossRefGoogle Scholar
Friedman, R., On threefolds with trivial canonical bundle, in Complex geometry and Lie theory (Sundance, UT, 1989), Proceedings of Symposia in Pure Mathematics, vol. 53 (American Mathematical Society, Providence, RI, 1991), 103–134.CrossRefGoogle Scholar
Fu, J., Li, J. and Yau, S.-T., Balanced metrics on non-Kähler Calabi–Yau threefolds, J. Differential Geom. 90 (2012), 81–129.CrossRefGoogle Scholar
Fu, J., Wang, Z. and Wu, D., Semilinear equations, the $\gamma _k$ function, and generalized Gauduchon metrics, J. Eur. Math. Soc. (JEMS) 15 (2013), 659–680.CrossRefGoogle Scholar
Fu, J. and Yau, S.-T., The theory of superstring with flux on non-Kähler manifolds and the complex Monge–Ampère equation, J. Differential Geom. 78 (2008), 369–428.CrossRefGoogle Scholar
Gauduchon, P., Le théorème de l'excentricité nulle, C. R. Acad. Sci. Paris 285 (1977), A387–A390.Google Scholar
Glasner, M., Stokes’ theorem and parabolicity of Riemannian manifolds, Proc. Amer. Math. Soc. 87 (1983), 70–72.Google Scholar
Hartshorne, R., Topological conditions for smoothing algebraic singularities, Topology 13 (1974), 241–253.CrossRefGoogle Scholar
Hull, C. M., Superstring compactifications with torsion and spacetime supersymmetry, Superunification and Extra Dimensions (Torino, 1985) (World Scientific, Singapore, 1986), 347–375.Google Scholar
Li, P., On some applications of Gauduchon metrics, Geom. Dedicata 213 (2021), 473–486.CrossRefGoogle Scholar
Li, J. and Yau, S.-T., Hermitian-Yang-Mills connection on non-Kähler manifolds, in Mathematical aspects of string theory (San Diego, Calif., 1986), Advanced Series in Mathematical Physics, vol. 1 (World Scientific, Singapore, 1987), 560–573.CrossRefGoogle Scholar
Lu, P. and Tian, G., The complex structure on a connected sum of $S^{3} \times S^{3}$ with trivial canonical bundle, Math. Ann. 298 (1994), 761–764.CrossRefGoogle Scholar
Michael, J. H. and Simon, L. M., Sobolev and mean-value inequalities on generalized submanifolds of $R^{n}$, Comm. Pure Appl. Math. 26 (1973), 361–379.CrossRefGoogle Scholar
Phong, D. H., Picard, S. and Zhang, X., Geometric flows and Strominger systems, Math. Z. 288 (2018), 101–113.CrossRefGoogle Scholar
Reid, M., The moduli space of $3$-folds with $K=0$ may nevertheless be irreducible, Math. Ann. 278 (1987), 329–334.CrossRefGoogle Scholar
Rossi, M., Geometric transitions, J. Geom. Phys. 56 (2006), 1940–1983.CrossRefGoogle Scholar
Ruan, W.-D. and Zhang, Y., Convergence of Calabi–Yau manifolds, Adv. Math. 228 (2011), 1543–1589.CrossRefGoogle Scholar
Skoda, H., Prolongement des courants, positifs, fermés de masse finie, Invent. Math. 66 (1982), 361–376.CrossRefGoogle Scholar
Strominger, A., Superstrings with torsion, Nuclear Phys. B 274 (1986), 253–284.CrossRefGoogle Scholar
Székelyhidi, G., Tosatti, V. and Weinkove, B., Gauduchon metrics with prescribed volume form, Acta Math. 219 (2017), 181–211.CrossRefGoogle Scholar
Tian, G., Smoothing 3-folds with trivial canonical bundle and ordinary double points, in Essays on mirror manifolds (International Press, Hong Kong, 1992), 458–479.Google Scholar
Tosatti, V. and Weinkove, B., The complex Monge–Ampère equation on compact Hermitian manifolds, J. Amer. Math. Soc. 23 (2010), 1187–1195.CrossRefGoogle Scholar
Ueno, K., Classification theory of algebraic varieties and compact complex spaces, Lecture Notes in Mathematics, vol. 439 (Springer, Berlin, 1975). Notes written in collaboration with P. Cherenack.CrossRefGoogle Scholar
Uhlenbeck, K. and Yau, S.-T., On the existence of Hermitian-Yang-Mills connections in stable vector bundles, in Proceedings of the symposium on Frontiers of the Mathematical Sciences: 1985, Communications on Pure and Applied Mathematics, vol. 39 (Wiley, New York, 1986), S257–S293.Google Scholar
Yau, S.-T., On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation. I, Comm. Pure Appl. Math. 31 (1978), 339–411.CrossRefGoogle Scholar
Yoshikawa, K.-i., Degeneration of algebraic manifolds and the spectrum of Laplacian, Nagoya Math. J. 146 (1997), 83–129.CrossRefGoogle Scholar