Article contents
Relation between two twisted inverse image pseudofunctors in duality theory
Published online by Cambridge University Press: 19 November 2014
Abstract
Grothendieck duality theory assigns to essentially finite-type maps 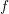 $f$ of noetherian schemes a pseudofunctor
$f$ of noetherian schemes a pseudofunctor 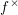 $f^{\times }$ right-adjoint to
$f^{\times }$ right-adjoint to 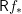 $\mathsf{R}f_{\ast }$, and a pseudofunctor
$\mathsf{R}f_{\ast }$, and a pseudofunctor 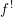 $f^{!}$ agreeing with
$f^{!}$ agreeing with 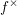 $f^{\times }$ when
$f^{\times }$ when 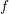 $f$ is proper, but equal to the usual inverse image
$f$ is proper, but equal to the usual inverse image 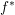 $f^{\ast }$ when
$f^{\ast }$ when 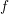 $f$ is étale. We define and study a canonical map from the first pseudofunctor to the second. This map behaves well with respect to flat base change, and is taken to an isomorphism by ‘compactly supported’ versions of standard derived functors. Concrete realizations are described, for instance for maps of affine schemes. Applications include proofs of reduction theorems for Hochschild homology and cohomology, and of a remarkable formula for the fundamental class of a flat map of affine schemes.
$f$ is étale. We define and study a canonical map from the first pseudofunctor to the second. This map behaves well with respect to flat base change, and is taken to an isomorphism by ‘compactly supported’ versions of standard derived functors. Concrete realizations are described, for instance for maps of affine schemes. Applications include proofs of reduction theorems for Hochschild homology and cohomology, and of a remarkable formula for the fundamental class of a flat map of affine schemes.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
- 6
- Cited by


