Published online by Cambridge University Press: 01 November 2007
Let F be a non-Archimedean local field and let p be the residual characteristic of F. Let G=GL2(F) and let P be a Borel subgroup of G. In this paper we study the restriction of irreducible smooth representations of G on 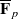 -vector spaces to P. We show that in a certain sense P controls the representation theory of G. We then extend our results to smooth
-vector spaces to P. We show that in a certain sense P controls the representation theory of G. We then extend our results to smooth 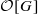 -modules of finite length and unitary K-Banach space representations of G, where
-modules of finite length and unitary K-Banach space representations of G, where 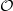 is the ring of integers of a complete discretely valued field K with residue field
is the ring of integers of a complete discretely valued field K with residue field 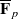 .
.