Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-09T06:40:24.072Z Has data issue: false hasContentIssue false
  • English
  • Français

On exact 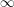$\infty$-categories and the Theorem of the Heart

Part of: Applied homological algebra and category theory Higher algebraic $K$-theory

Published online by Cambridge University Press:  19 August 2015

Clark Barwick
Clark Barwick*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Building 2, 77 Massachusetts Avenue, Cambridge, MA 02139-4307, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The new homotopy theory of exact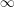$\infty$-categories is introduced and employed to prove a Theorem of the Heart for algebraic 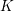$K$-theory (in the sense of Waldhausen). This implies a new compatibility between Waldhausen 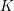$K$-theory and Neeman 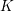$K$-theory. Additionally, it provides a new proof of the Dévissage and Localization theorems of Blumberg–Mandell, new models for the 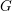$G$-theory of schemes, and a proof of the invariance of 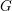$G$-theory under derived nil-thickenings.

Keywords

algebraic K-theorystable ∞-categoriest-structures

MSC classification

Primary: 19D99: None of the above, but in this section 55U40: Topological categories, foundations of homotopy theory
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 11 , November 2015 , pp. 2160 - 2186
Copyright
© The Author 2015 

References

Arinkin, D. and Bezrukavnikov, R., Perverse coherent sheaves, Mosc. Math. J. 10 (2010), 3–29; 271; MR 2668828 (2011g:14040).CrossRefGoogle Scholar
Baker, A. and Richter, B., Uniqueness of E ∞ structures for connective covers, Proc. Amer. Math. Soc. 136 (2008), 707–714; MR 2358512 (2008m:55017).CrossRefGoogle Scholar
Barwick, C., On the algebraic $K$-theory of higher categories, J. Topol., to appear,arXiv:1204.3607.Google Scholar
Barwick, C. and Lawson, T., Regularity of structured ring spectra and localization in $K$-theory, Preprint (2014), arXiv:1402.6038.Google Scholar
Barwick, C. and Schommer-Pries, C., On the unicity of the homotopy theory of higher categories, Preprint (2011), arXiv:1112.0040.Google Scholar
Blumberg, A. J., Gepner, D. and Tabuada, G., A universal characterization of higher algebraic K-theory, Geom. Topol. 17 (2013), 733–838, doi:10.2140/gt.2013.17.733.CrossRefGoogle Scholar
Blumberg, A. J. and Mandell, M. A., The localization sequence for the algebraic K-theory of topological K-theory, Acta Math. 200 (2008), 155–179; MR 2413133 (2009f:19003).CrossRefGoogle Scholar
Joyal, A., Notes on quasi-categories, Preprint (2008).Google Scholar
Joyal, A., The theory of quasi-categories and its applications, Advanced Course on Simplicial Methods in Higher Categories, Vol. 2, Quaderns, vol. 45 (Centre de Recerca Matemàtica, Barcelona, 2008).Google Scholar
Keller, B., Chain complexes and stable categories, Manuscripta Math. 67 (1990), 379–417; MR 1052551 (91h:18006).CrossRefGoogle Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009); MR 2522659 (2010j:18001).Google Scholar
Lurie, J., $(\infty ,2)$-categories and the Goodwillie calculus I, Preprint (2009).Google Scholar
Lurie, J., Derived algebraic geometry VIII. Quasi-coherent sheaves and Tannaka duality theorems, Preprint (2011).Google Scholar
Lurie, J., Higher algebra, Preprint (2012).Google Scholar
Neeman, A., K-theory for triangulated categories. I(A). Homological functors, Asian J. Math. 1 (1997), 330–417; MR 1491990 (99m:18008a).CrossRefGoogle Scholar
Neeman, A., K-theory for triangulated categories. I(B). Homological functors, Asian J. Math. 1 (1997), 435–529; MR 1604910 (99m:18008b).CrossRefGoogle Scholar
Neeman, A., K-theory for triangulated categories. II. The subtlety of the theory and potential pitfalls, Asian J. Math. 2 (1998), 1–125; MR 1656552 (2000m:19008).CrossRefGoogle Scholar
Neeman, A., K-theory for triangulated categories. III(A). The theorem of the heart, Asian J. Math. 2 (1998), 495–589; MR 1724625.CrossRefGoogle Scholar
Neeman, A., K-theory for triangulated categories. III(B). The theorem of the heart, Asian J. Math. 3 (1999), 557–608; MR 1793672.CrossRefGoogle Scholar
Neeman, A., K-theory for triangulated categories 3½. A. A detailed proof of the theorem of homological functors, K-Theory 20 (2000), 97–174; special issues dedicated to Daniel Quillen on the occasion of his sixtieth birthday, Part II; MR 1798824 (2002b:18014).CrossRefGoogle Scholar
Neeman, A., K-theory for triangulated categories 3½. B. A detailed proof of the theorem of homological functors, K-Theory 20 (2000), 243–298; special issues dedicated to Daniel Quillen on the occasion of his sixtieth birthday, Part III; MR 1798828 (2002b:18015).CrossRefGoogle Scholar
Neeman, A., K-theory for triangulated categories 3¾: a direct proof of the theorem of the heart, K-Theory 22 (2001), 1–144; MR 1828612 (2002f:19004).CrossRefGoogle Scholar
Neeman, A., The K-theory of triangulated categories, Handbook of K-Theory, vols 1, 2 (Springer, Berlin, 2005), 1011–1078; MR 2181838 (2006g:19004).Google Scholar
Schlichting, M., A note on K-theory and triangulated categories, Invent. Math. 150 (2002), 111–116; MR 1930883 (2003h:18015).CrossRefGoogle Scholar
Thomason, R. W. and Trobaugh, T., Higher algebraic K-theory of schemes and of derived categories, in The Grothendieck festschrift, Vol. III, Progress in Mathematics, vol. 88 (Birkhäuser, Boston, MA, 1990), 247–435; MR 92f:19001.CrossRefGoogle Scholar
Toën, B., Vers une axiomatisation de la théorie des catégories supérieures, K-Theory 34 (2005), 233–263; MR 2182378 (2006m:55041).CrossRefGoogle Scholar
Waldhausen, F., Algebraic K-theory of spaces, in Algebraic and geometric topology (New Brunswick, NJ, 1983), Lecture Notes in Mathematics, vol. 1126 (Springer, Berlin, 1985), 318–419; MR 86m:18011.CrossRefGoogle Scholar
Yekutieli, A. and Zhang, J. J., Dualizing complexes and perverse sheaves on noncommutative ringed schemes, Selecta Math. (N.S.) 12 (2006), 137–177; MR 2244264 (2008d:14004).CrossRefGoogle Scholar