Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-04T21:32:01.605Z Has data issue: false hasContentIssue false
  • English
  • Français

A new upper bound for sets with no square differences

Part of: Diophantine equations Additive number theory; partitions Sequences and sets

Published online by Cambridge University Press:  30 September 2022

Thomas F. Bloom  and
James Maynard
Thomas F. Bloom
Affiliation:
Mathematical Institute, Woodstock Road, Oxford OX2 6GG, UK [email protected]
James Maynard
Affiliation:
Mathematical Institute, Woodstock Road, Oxford OX2 6GG, UK [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that if 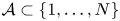$\mathcal {A}\subset \{1,\ldots,N\}$ has no solutions to 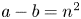$a-b=n^2$ with 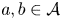$a,b\in \mathcal {A}$ and 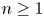$n\geq 1$, then

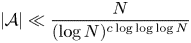\[ \lvert \mathcal{A}\rvert \ll \frac{N}{(\log N)^{c\log\log \log N}} \]
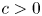for some absolute constant $c>0$. This improves upon a result of Pintz, Steiger, and Szemerédi.

Keywords

additive combinatoricssquaresdifference setdensity increment

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity 11P55: Applications of the Hardy-Littlewood method 11D09: Quadratic and bilinear equations
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 8 , August 2022 , pp. 1777 - 1798
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

T.B. was supported by a postdoctoral grant funded by the Royal Society held at the University of Cambridge. J.M. was supported by a Royal Society Wolfson Merit Award, and funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No 851318).

References

Balog, A., Pelikan, J., Pintz, J. and Szemerédi, E., Difference sets without $k$th powers, Acta Math. Hungar. 65 (1994), 165–187.CrossRefGoogle Scholar
Bloom, T. F. and Sisask, O., Breaking the logarithmic barrier in Roth's theorem on arithmetic progressions, Preprint (2021), arXiv:2007.03528.Google Scholar
Bourgain, J., Dilworth, S. J., Ford, K., Konyagin, S. V. and Kutzarova, D., Breaking the $k^2$ barrier for explicit RIP matrices, in STOC’11 – Proceedings of the 43rd ACM Symposium on Theory of Computing (ACM, 2011), 637–644.CrossRefGoogle Scholar
Chang, M.-C., A polynomial bound in Freiman's theorem, Duke Math. J. 113 (2002), 399–419.CrossRefGoogle Scholar
Furstenberg, H., Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions, J. Anal. Math. 31 (1977), 204–256.CrossRefGoogle Scholar
Green, B., Sárkzözy's theorem in function fields, Q. J. Math. 68 (2017), 237–242.CrossRefGoogle Scholar
Lewko, M., An improved lower bound related to the Furstenberg–Sárközy theorem, Electron. J. Combin. 22 (2015), Paper 1.32.CrossRefGoogle Scholar
Maynard, J., Fractional parts of polynomials, Preprint (2020), arXiv:2011.12275.Google Scholar
Montgomery, H. L., Mean and large values of Dirichlet polynomials, Invent. Math. 8 (1969), 334–345.CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I. Classical Theory (Cambridge University Press, Cambridge, 2007).Google Scholar
Pintz, J., Steiger, W. L. and Szemerédi, E., On sets of natural numbers whose difference set contains no squares, J. Lond. Math. Soc. (2) 37 (1988), 219–231.CrossRefGoogle Scholar
Rice, A., A maximal extension of the best-known bounds for the Furstenberg–Sárközy theorem, Acta Arith. 187 (2019), 1–41.CrossRefGoogle Scholar
Ruzsa, I., Difference sets without squares, Period. Math. Hungar. 15 (1984), 205–209.CrossRefGoogle Scholar
Ruzsa, I. and Sanders, T., Difference sets and the primes, Acta Arith. 131 (2008), 281–301.CrossRefGoogle Scholar
Sárközy, A., On difference sets of sequences of integers. I, Acta Math. Acad. Sci. Hungar. 31 (1978), 125–149.CrossRefGoogle Scholar
Wolf, J., Arithmetic structure in sets of integers, PhD thesis, University of Cambridge (2008), https://doi.org/10.17863/CAM.16214.CrossRefGoogle Scholar