Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T23:06:36.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed motivic sheaves (and weights for them) exist if ‘ordinary’ mixed motives do

Part of: Homological algebra Abelian categories $K$-theory in geometry Commutative algebra: Homological methods Cycles and subschemes (Co)homology theory

Published online by Cambridge University Press:  09 January 2015

Mikhail V. Bondarko
Mikhail V. Bondarko*
Affiliation:
Department of Mathematics and Mechanics, St. Petersburg State University, Bibliotechnaya Pl. 2, 198904, St. Petersburg, Russia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The goal of this paper is to prove that if certain ‘standard’ conjectures on motives over algebraically closed fields hold, then over any ‘reasonable’ scheme 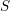$S$ there exists a motivic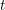$t$-structure for the category 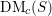$\text{DM}_{c}(S)$ of relative Voevodsky’s motives (to be more precise, for the Beilinson motives described by Cisinski and Deglise). If 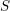$S$ is of finite type over a field, then the heart of this 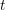$t$-structure (the category of mixed motivic sheaves over 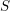$S$) is endowed with a weight filtration with semisimple factors. We also prove a certain ‘motivic decomposition theorem’ (assuming the conjectures mentioned) and characterize semisimple motivic sheaves over 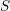$S$ in terms of those over its residue fields. Our main tool is the theory of weight structures. We actually prove somewhat more than the existence of a weight filtration for mixed motivic sheaves: we prove that the motivic 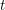$t$-structure is transversal to the Chow weight structure for 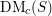$\text{DM}_{c}(S)$ (that was introduced previously by Hébert and the author). We also deduce several properties of mixed motivic sheaves from this fact. Our reasoning relies on the degeneration of Chow weight spectral sequences for ‘perverse étale homology’ (which we prove unconditionally); this statement also yields the existence of the Chow weight filtration for such (co)homology that is strictly restricted by (‘motivic’) morphisms.

Keywords

motivesmixed motivic sheavesperverse sheavesétale homologytriangulated categoriesweight structuresweight filtrationdecomposition theorem

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives
Secondary: 14F42: Motivic cohomology; motivic homotopy theory 19E15: Algebraic cycles and motivic cohomology 14F43: Other algebro-geometric (co)homologies (e.g., intersection, equivariant, Lawson, Deligne (co)homologies) 18G40: Spectral sequences, hypercohomology 14C25: Algebraic cycles 14F20: Étale and other Grothendieck topologies and (co)homologies 18E30: Derived categories, triangulated categories 13D15: Grothendieck groups, $K$-theory
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 5 , May 2015 , pp. 917 - 956
Copyright
© The Author 2015 

References

Ayoub, J., The motivic vanishing cycles and the conservation conjecture, in Algebraic cycles and motives, Vol. 1, London Mathematical Society Lecture Note Series, vol. 343, eds Nagel, J., Peters, C. and Murre, J. P. (Cambridge University Press, Cambridge, 2007), 3–54.CrossRefGoogle Scholar
Barbieri-Viale, L. and Kahn, B., On the derived category of 1-motives, Preprint (2014),http://www.math.jussieu.fr/∼kahn/preprints/revder1mot1.pdf.Google Scholar
Beilinson, A., Height pairing between algebraic cycles, in K-theory, arithmetic and geometry, Lecture Notes in Mathematics, vol. 1289 (Springer, 1987), 1–26.Google Scholar
Beilinson, A., Remarks on n-motives and correspondences at the generic point, in Motives, polylogarithms and Hodge theory, Part I, Irvine, CA, 1998, International Press Lecture Series, 3, vol. I (International Press, Somerville, MA, 2002), 35–46.Google Scholar
Beilinson, A., Remarks on Grothendieck’s standard conjectures, in Regulators III, Proceedings of the conference held at the University of Barcelona, July 11–23, 2010, Contemporary Mathematics, vol. 571, eds Burgos, J. I. and Lewis, J. (American Mathematical Society, Providence, RI, 2012), 25–32.Google Scholar
Beilinson, A., Bernstein, J. and Deligne, P., Faisceaux pervers, Astérisque 100 (1982), 5–171.Google Scholar
Bondarko, M. V., Differential graded motives: weight complex, weight filtrations and spectral sequences for realizations; Voevodsky vs. Hanamura, J. Inst. Math. Jussieu 8 (2009), 39–97; see also arXiv:math.AG/0601713.CrossRefGoogle Scholar
Bondarko, M., Weight structures vs. t-structures; weight filtrations, spectral sequences, and complexes (for motives and in general), J. K-Theory 6 (2010), 387–504; see alsoarXiv:0704.4003.CrossRefGoogle Scholar
Bondarko, M. V., Motivically functorial coniveau spectral sequences; direct summands of cohomology of function fields, Doc. Math. (2010), 33–117; extra volume: Andrei Suslin’s Sixtieth Birthday.Google Scholar
Bondarko, M. V., ℤ[1∕p]-motivic resolution of singularities, Compositio Math. 147 (2011), 1434–1446.CrossRefGoogle Scholar
Bondarko, M. V., Weight structures and ‘weights’ on the hearts of t-structures, Homology, Homotopy Appl. 14 (2012), 239–261.CrossRefGoogle Scholar
Bondarko, M. V., Weights for relative motives: relation with mixed complexes of sheaves, Int. Math. Res. Not. IMRN 2014 (2014), 4715–4767; doi:10.1093/imrn/rnt088.CrossRefGoogle Scholar
Cisinski, D. and Déglise, F., Triangulated categories of mixed motives, Preprint (2009),arXiv:0912.2110.Google Scholar
Cisinski, D. and Déglise, F., Étale motives, Compositio Math., to appear, arXiv:1305.5361v3.Google Scholar
Corti, A. and Hanamura, M., Motivic decomposition and intersection Chow groups, I, Duke Math. J. 103 (2000), 459–522.Google Scholar
Dieudonné, J. and Grothendieck, A., Eléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas, Troisiéme Partie, Publ. Math. Inst. Hautes Études Sci. 28 (1966).Google Scholar
Ekedahl, T., On the adic formalism, in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, 1990), 197–218.Google Scholar
Freitag, E. and Kiehl, R., Etale cohomology and the Weil conjecture (Springer, 1988), 343.CrossRefGoogle Scholar
Hanamura, M., Mixed motives and algebraic cycles, III, Math. Res. Lett. 6 (1999), 61–82.CrossRefGoogle Scholar
Hébert, D., Structures de poids la Bondarko sur les motifs de Beilinson, Compositio Math. 147 (2011), 1447–1462.CrossRefGoogle Scholar
Huber, A., Mixed perverse sheaves for schemes over number fields, Compositio Math. 108 (1997), 107–121.CrossRefGoogle Scholar
Huber, A. and Kahn, B., The slice filtration and mixed Tate motives, Compositio Math. 142 (2006), 907–936.CrossRefGoogle Scholar
Illusie, L., Laszlo, Y. and Orgogozo, F., Travaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents (Séminaire à l’École polytechnique 2006–2008), Astérisque, vol. 363–364 (Société Mathématique de France, 2014).Google Scholar
Ito, T., Weight-monodromy conjecture over equal characteristic local fields, Amer. J. Math. 127 (2005), 647–658.CrossRefGoogle Scholar
Jannsen, U., Motives, numerical equivalence and semisimplicity, Invent. Math. 107 (1992), 447–452.CrossRefGoogle Scholar
Kleinman, S., The standard conjectures, in Motives, Proceedings of Symposia in Pure Mathematics, vol. 55, Part 1 (American Mathematical Society, Providence, RI, 1994), 3–20.CrossRefGoogle Scholar
Neeman, A., Triangulated categories, Annals of Mathematics Studies, vol. 148 (Princeton University Press, Princeton, NJ, 2001).CrossRefGoogle Scholar
Popescu, D., General Néron desingularization and approximation, Nagoya Math. J. 104 (1986), 85–115.CrossRefGoogle Scholar
Scholbach, J., f-cohomology and motives over number rings, Kodai Math. J. 35 (2012), 1–32.CrossRefGoogle Scholar
Grothendieck, A., Expose VIII, in Séminaire de Géométrie Algébrique du Bois Marie 1963–1964, Théorie des topos et cohomologie étale des schémas (SGA 4), Tome 2, Lecture Notes in Mathematics, vol. 270 (Springer, 1972).Google Scholar
Deligne, P., Expose XVIII, in Séminaire de Géométrie Algébrique du Bois Marie 1963–1964, Théorie des topos et cohomologie étale des schémas (SGA 4), Tome 3, Lecture Notes in Mathematics, vol. 305 (Springer, 1973).Google Scholar
Silverman, J., Advanced topics in the arithmetic of elliptic curves (Springer, 1994).CrossRefGoogle Scholar
Smirnov, O., Graded associative algebras and Grothendieck standard conjectures, Invent. Math. 128 (1997), 201–206.CrossRefGoogle Scholar
Voevodsky, V., Triangulated categories of motives over a field, in Cycles, transfers and motivic homology theories, Annals of Mathematical Studies, vol. 143, eds Voevodsky, V., Suslin, A. and Friedlander, E. (Princeton University Press, Princeton, NJ, 2000), 188–238.Google Scholar
Wildeshaus, J., Notes on Artin–Tate motives, Preprint (2008), http://www.math.uiuc.edu/K-theory/0918/.Google Scholar
Wildeshaus, J., Intermediate extension of Chow motives of Abelian type, Preprint (2012),arXiv:1211.5327.Google Scholar