Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-22T06:11:53.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Local and global structure of connections on nonarchimedean curves

Part of: Differential and difference algebra Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  07 January 2015

Kiran S. Kedlaya
Kiran S. Kedlaya*
Affiliation:
Department of Mathematics, University of California, San Diego, 9500 Gilman Drive #0112, La Jolla, CA 92093, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a vector bundle with connection on a 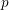$p$-adic analytic curve in the sense of Berkovich. We collect some improvements and refinements of recent results on the structure of such connections, and on the convergence of local horizontal sections. This builds on work from the author’s 2010 book and on subsequent improvements by Baldassarri and by Poineau and Pulita. One key result exclusive to this paper is that the convergence polygon of a connection is locally constant around every type 4 point.

Keywords

p-adic differential equationsradius of convergenceconvergence polygonnonarchimedean analytic spaces

MSC classification

Primary: 12H25: $p$-adic differential equations 14G22: Rigid analytic geometry
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 6 , June 2015 , pp. 1096 - 1156
Copyright
© The Author 2015 

References

André, Y., Filtrations de type Hasse-Arf et monodromie p-adique, Invent. Math. 148 (2002), 285–317.Google Scholar
André, Y., Slope filtrations, Confluentes Math. 1 (2009), 1–85.CrossRefGoogle Scholar
Baker, M., Payne, S. and Rabinoff, J., Nonarchimedean geometry, tropicalization, and metrics on curves, Preprint (2012), arXiv:1104.0320v2.Google Scholar
Baker, M. and Rumely, R., Potential theory and dynamics on the Berkovich projective line, AMS Surveys and Monographs, vol. 159 (American Mathematical Society, Providence, RI, 2010).CrossRefGoogle Scholar
Baldassarri, F., Continuity of the radius of convergence of differential equations on p-adic analytic curves, Invent. Math. 182 (2010), 513–584.CrossRefGoogle Scholar
Baldassarri, F. and Di Vizio, L., Continuity of the radius of convergence of $p$-adic differential equations on Berkovich spaces, Preprint (2007), arXiv:0709.2008v1.Google Scholar
Baldassarri, F. and Kedlaya, K. S., Harmonic functions attached to meromorphic connections on non-archimedean curves, in preparation.Google Scholar
Bellovin, R., $p$-adic Hodge theory in rigid analytic families, Preprint (2013), arXiv:1306.5685v1.CrossRefGoogle Scholar
Berkovich, V., Spectral theory and analytic geometry over non-Archimedean fields, Surveys and Monographs, vol. 33 (American Mathematical Society, Providence, RI, 1990).Google Scholar
Berkovich, V. G., Étale cohomology for non-Archimedean analytic spaces, Publ. Math. Inst. Hautes Études Sci. 78 (1993), 5–161.CrossRefGoogle Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean analysis, Grundlehren der Mathematischen Wissenschaften, vol. 261 (Springer, Berlin, 1984).CrossRefGoogle Scholar
Bourbaki, N., Topologie Générale, Chapitres 1 à 4 (Hermann, Paris, 1971).Google Scholar
Christol, G. and Mebkhout, Z., Sur le théorème de l’indice des quations différentielles, Ann. Inst. Fourier 43 (1993), 1545–1574.CrossRefGoogle Scholar
Christol, G. and Mebkhout, Z., Sur le théorème de l’indice des quations différentielles, II, Ann. of Math. (2) 146 (1997), 345–410.CrossRefGoogle Scholar
Christol, G. and Mebkhout, Z., Sur le théorème de l’indice des quations différentielles, III, Ann. of Math. (2) 151 (2000), 385–457.CrossRefGoogle Scholar
Christol, G. and Mebkhout, Z., Sur le théorème de l’indice des quations différentielles, IV, Invent. Math. 143 (2001), 629–672.CrossRefGoogle Scholar
Curtis, C. W. and Reiner, I., Representation theory of finite groups and associative algebras, reprint of the 1962 original (American Mathematical Society, Providence, RI, 2006).Google Scholar
de Jong, A. J., Étale fundamental groups of non-Archimedean analytic spaces, Compositio Math. 97 (1995), 89–118.Google Scholar
Ducros, A., La structure des courbes analytiques, in preparation, version of 12 Feb 2014 downloaded from http://www.math.jussieu.fr/∼ducros/livre.html.Google Scholar
Dwork, B. and Robba, P., On ordinary linear p-adic differential equations, Trans. Amer. Math. Soc. 231 (1977), 1–46.Google Scholar
Faber, X., Topology and geometry of the Berkovich ramification locus for rational functions, Manuscripta Math. 142 (2013), 439–474.CrossRefGoogle Scholar
Faber, X., Topology and geometry of the Berkovich ramification locus for rational functions, II, Math. Ann. 356 (2013), 819–844.CrossRefGoogle Scholar
Kedlaya, K. S., A p-adic local monodromy theorem, Ann. of Math. (2) 160 (2004), 93–184.CrossRefGoogle Scholar
Kedlaya, K. S., Local monodromy of p-adic differential equations: an overview, Int. J. Number Theory 1 (2005), 109–154; errata at http://kskedlaya.org/papers/.CrossRefGoogle Scholar
Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals, I: Unipotence and logarithmic extensions, Compositio Math. 143 (2007), 1164–1212.CrossRefGoogle Scholar
Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals, II: A valuation-theoretic approach, Compositio Math. 144 (2008), 657–672.CrossRefGoogle Scholar
Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals, III: Local semistable reduction at monomial valuations, Compositio Math. 145 (2009), 143–172.CrossRefGoogle Scholar
Kedlaya, K. S., p-adic differential equations (Cambridge University Press, Cambridge, 2010), errata posted at http://kskedlaya.org/papers.CrossRefGoogle Scholar
Kedlaya, K. S., Good formal structures for flat meromorphic connections, I: Surfaces, Duke Math. J. 154 (2010), 343–418; Erratum, Duke Math. J. 161 (2012), 733–734.CrossRefGoogle Scholar
Kedlaya, K. S., Good formal structures for flat meromorphic connections, II: Excellent schemes, J. Amer. Math. Soc. 24 (2011), 183–229.CrossRefGoogle Scholar
Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals, IV: Local semistable reduction at nonmonomial valuations, Compositio Math. 147 (2011), 467–523.CrossRefGoogle Scholar
Kedlaya, K. S., Nonarchimedean geometry of Witt vectors, Nagoya Math. J. 209 (2013), 111–165.CrossRefGoogle Scholar
Kedlaya, K. S., Pottharst, J. and Xiao, L., Cohomology of arithmetic families of (𝜙, Γ)-modules, J. Amer. Math. Soc. 27 (2014), 1043–1115.CrossRefGoogle Scholar
Kedlaya, K. S. and Xiao, L., Differential modules on p-adic polyannuli, J. Inst. Math. Jussieu 9 (2010), 155–201.CrossRefGoogle Scholar
Mebkhout, Z., Analogue p-adique du théorème de Turrittin et le théorème de la monodromie p-adique, Invent. Math. 148 (2002), 319–351.CrossRefGoogle Scholar
Payne, S., Analytification is the limit of all tropicalizations, Math. Res. Lett. 16 (2009), 543–556.CrossRefGoogle Scholar
Poineau, J., Les espaces de Berkovich sont angéliques, Bull. Soc. Math. France 141 (2013), 267–297.CrossRefGoogle Scholar
Poineau, J. and Pulita, A., The convergence Newton polygon of a $p$-adic differential equation II: Continuity and finiteness on Berkovich curves, Preprint (2012), arXiv:1209.3663v1.Google Scholar
Poineau, J. and Pulita, A., Continuity and finiteness of the radius of convergence of a $p$-adic differential equation via potential theory, Preprint (2012), arXiv:1209.6276v1.Google Scholar
Poineau, J. and Pulita, A., The convergence Newton polygon of a $p$-adic differential equation III: Global decomposition and controlling graphs, Preprint (2013), arXiv:1308.0859v1.Google Scholar
Poineau, J. and Pulita, A., The convergence Newton polygon of a $p$-adic differential equation IV: Local and global index theorems, Preprint (2013), arXiv:1309.3940v1.Google Scholar
Pulita, A., The convergence Newton polygon of a $p$-adic differential equation I: Affinoid domains of the Berkovich affine line, Preprint (2014), arXiv:1208.5850v4.CrossRefGoogle Scholar
Robba, P., On the index of p-adic differential operators, I, Ann. of Math. (2) 101 (1975), 280–316.CrossRefGoogle Scholar
Robba, P., On the index of p-adic differential operators, II, Duke Math. J. 43 (1976), 19–31.CrossRefGoogle Scholar
Robba, P., On the index of p-adic differential operators, III: Application to twisted exponential sums, Astérisque 119–120 (1984), 191–266.Google Scholar
Robba, P., Indice d’un operateur differentiel p-adique, IV, Cas de systèmes. Mesure de l’irrégularité dans un disque, Ann. Inst. Fourier 35 (1985), 13–55.CrossRefGoogle Scholar
Saavedra Rivano, N., Catégories Tannakiennes, Lecture Notes in Mathematics, vol. 265 (Springer, Berlin, 1972).CrossRefGoogle Scholar
Schneider, P. and Teitelbaum, J., Algebras of p-adic distributions and admissible representation, Invent. Math. 153 (2003), 145–196.CrossRefGoogle Scholar
Serre, J.-P., Local fields, Graduate Texts in Mathematics, vol. 67 (Springer, New York, 1979).CrossRefGoogle Scholar
Vaquié, M., Valuations, in Resolution of singularities, Obergurgl, 1997, Progress in Mathematics, vol. 181 (Birkhäuser, Basel, 2000), 539–590.Google Scholar
Xiao, L., Non-archimedean differential modules and ramification theory, Thesis, Massachusetts Institute of Technology, 2009.Google Scholar
Xiao, L., On the refined ramification filtrations in the equal characteristic case, Algebra Number Theory 6 (2012), 1579–1667.CrossRefGoogle Scholar