Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T06:53:28.376Z Has data issue: false hasContentIssue false
  • English
  • Français

La conjecture de Tate entière pour les cubiques de dimension quatre

Part of: Surfaces and higher-dimensional varieties Cycles and subschemes Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  16 October 2014

François Charles  and
Alena Pirutka
François Charles
Affiliation:
Département de Mathématiques, Université Paris-Sud, Bâtiment 425, 91405 Orsay cedex, France email [email protected]
Alena Pirutka
Affiliation:
Université de Strasbourg, IRMA – UMR 7501 du CNRS, 7 rue René Descartes, 67084 Strasbourg cedex, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove the integral Tate conjecture for cycles of codimension 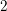$2$ on smooth cubic fourfolds over an algebraic closure of a field finitely generated over its prime subfield and of characteristic different from 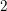$2$ or 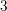$3$. The proof relies on the Tate conjecture with rational coefficients, proved in that setting by the first author, and on an argument of Voisin coming from complex geometry.

Résumé

Dans ce texte, on établit une version entière de la conjecture de Tate pour les cycles de codimension 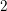$2$ sur une hypersurface cubique lisse 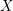$X$ de 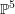$\mathbb{P}^{5}$ sur une clôture algébrique d’un corps de type fini sur son sous-corps premier et de caractéristique différente de 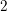$2$ et 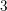$3$. La preuve s’appuie sur la conjecture de Tate à coefficients rationnels prouvée dans ce cas par le premier auteur et sur un argument de géométrie complexe dû à Voisin.

Keywords

conjecture de Tatecubique de dimension 4jacobienne intermédiairefonction normale

MSC classification

Primary: 14C25: Algebraic cycles 14G15: Finite ground fields 14J70: Hypersurfaces
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 2 , February 2015 , pp. 253 - 264
Copyright
© The Author(s) 2014 

References

Altman, A. and Kleiman, S., Foundations of the theory of Fano schemes, Composito Math. 34 (1977), 3–47.Google Scholar
André, Y., On the Shafarevich and Tate conjectures for hyper-Kähler varieties, Math. Ann. 305 (1996), 205–248.Google Scholar
Atiyah, M. F. and Hirzebruch, F., Analytic cycles on complex manifolds, Topology 1 (1962), 25–45.Google Scholar
Beilinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers, in Analyse et topologie sur les espaces singuliers I (Luminy, 1981), Astérisque, vol. 100 (Société Mathématique de France, Paris, 1982), 5–171.Google Scholar
Bloch, S., Algebraic cycles and values of L-functions, J. Reine Angew. Math. 350 (1984), 94–108.Google Scholar
Charles, F., On the zero locus of normal functions and the étale Abel–Jacobi map, Int. Math. Res. Not. IMRN 2010(12) (2010), 2283–2304.Google Scholar
Charles, F., The Tate conjecture for K3 surfaces over finite fields, Invent. Math. 194 (2013), 119–145.CrossRefGoogle Scholar
Clemens, H. and Griffiths, P., The intermediate Jacobian of the cubic threefold, Ann. of Math. (2) 95 (1972), 281–356.Google Scholar
Colliot-Thélène, J.-L. and Kahn, B., Cycles de codimension 2 et H 3 non ramifié pour les variétés sur les corps finis, J. K-Theory 11 (2013), 1–53.Google Scholar
Colliot-Thélène, J. L. and Szamuely, T., Autour de la conjecture de Tate à coefficients ℤℓsur les corps finis, in The geometry of algebraic cycles, Clay Mathematics Proceedings, vol. 9, eds Akhtar, R., Brosnan, P. and Joshua, R. (American Mathematical Society, Providence, RI, 2010), 83–98.Google Scholar
Colliot-Thélène, J.-L. and Voisin, C., Cohomologie non ramifiée et conjecture de Hodge entière, Duke Math. J. 161 (2012), 735–801.Google Scholar
Drezet, J.-M. and Narasimhan, M. S., Groupe de Picard des variétés de modules de fibrés semi-stables sur les courbes algébriques, Invent. Math. 97 (1989), 53–94.Google Scholar
Druel, S., Espace des modules des faisceaux de rang 2 semi-stables de classes de Chern c 1= 0, c 2= 2 et c 3= 0 sur la cubique de ℙ4, Int. Math. Res. Not. IMRN 2000 (2000), 985–1004.Google Scholar
Faltings, G., Complements to Mordell, in Rational points (Bonn, 1983/1984), Aspects of Mathematics, vol. E6 (Vieweg, Braunschweig, 1984), 203–227.Google Scholar
Griffiths, P., Periods of integrals on algebraic manifolds, I; II, Amer. J. Math. 90 (1968), 568–626; 805–865.Google Scholar
Grothendieck, A., Techniques de construction et théorèmes d’existence en géométrie algébrique IV: les schémas de Hilbert, Séminaire Bourbaki 6 (1960–1961), 249–276; Exposé no. 221.Google Scholar
Höring, A. and Voisin, C., Anticanonical divisors and curve classes on Fano manifolds, Pure Appl. Math. Q. 7 (2011), 1371–1393.CrossRefGoogle Scholar
Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves, Cambridge Mathematical Library, second edition (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Jannsen, U., Continuous étale cohomology, Math. Ann. 280 (1988), 207–245; J. Inst. Math. Jussieu 1 (2002), 467–476.Google Scholar
Kleiman, S., The Picard scheme, in Fundamental algebraic geometry: Grothendieck’s FGA explained, Mathematical Surveys and Monographs, vol. 123 (American Mathematical Society, Providence, RI, 2005), 235–321.Google Scholar
Langer, A., Moduli spaces of sheaves in mixed characteristic, Duke Math. J. 124 (2004), 571–586.Google Scholar
Langer, A., Semistable sheaves in positive characteristic, Ann. of Math. (2) 159 (2004), 251–276.Google Scholar
Madapusi Pera, K., The Tate conjecture for $K3$ surfaces in odd characteristic, Preprint (2013), arXiv:1301.6326, http://www.math.harvard.edu/∼keerthi/papers/tate.pdf.Google Scholar
Markushevich, D. and Tikhomirov, A., The Abel-Jacobi map of a moduli component of vector bundles on the cubic threefold, J. Algebraic Geom. 10 (2001), 37–62.Google Scholar
Mumford, D., Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 34 (Springer, Berlin, 1965).Google Scholar
Nishimura, H., Some remarks on rational points, Mem. Coll. Sci. Univ. Kyoto. Ser. A. Math. 29 (1955), 189–192.Google Scholar
Parimala, R. and Suresh, V., Degree three cohomology of function fields of surfaces, Preprint (2010), arXiv:1012.5367.Google Scholar
Pirutka, A., Sur le groupe de Chow de codimension deux des variétés sur les corps finis, Algebra Number Theory 5 (2011), 803–817.Google Scholar
Raskind, W., Higher ℓ-adic Jacobi mappings and filtrations on Chow groups, Duke Math. J. 78 (1995), 33–57.Google Scholar
Schoen, C., An integral analog of the Tate conjecture for one-dimensional cycles on varieties over finite fields, Math. Ann. 311 (1998), 493–500.Google Scholar
Serre, J.-P., Cohomologie galoisienne, Lecture Notes in Mathematics, vol. 5, fifth edition (Springer, Berlin, 1994).Google Scholar
Deligne, P. and Katz, N. (eds), Groupes de monodromie en géométrie algébrique, in Séminaire de géométrie algébrique du bois marie 1967–1969 (SGA 7 II), Lecture Notes in Mathematics, vol. 340 (Springer, Berlin, 1973).Google Scholar
Tate, J., Algebraic cycles and poles of zeta functions, in Arithmetical algebraic geometry: proceedings of a conference held at Purdue University December 5–7, 1963 (Harper and Row, New York, 1965), 93–110.Google Scholar
Voisin, C., Théorie de Hodge et géométrie algébrique complexe, Cours spécialisés, vol. 10 (Société Mathématique de France, Paris, 2002).Google Scholar
Voisin, C., On integral Hodge classes on uniruled and Calabi-Yau threefolds, in Moduli spaces and arithmetic geometry (Kyoto, 2004), Advanced Studies in Pure Mathematics, vol. 45 (Mathematical Society of Japan, Tokyo, 2006), 43–73.CrossRefGoogle Scholar
Voisin, C., Some aspects of the Hodge conjecture, Jpn. J. Math. 2 (2007), 261–296.Google Scholar
Voisin, C., Remarks on curve classes on rationally connected varieties, in A celebration of algebraic geometry: a conference in honor of Joe Harris’ 60th birthday, Clay Mathematics Proceedings, vol. 18 (American Mathematical Society, Providence, RI, 2013), 591–599.Google Scholar
Voisin, C., Abel-Jacobi map, integral Hodge classes and decomposition of the diagonal, J. Algebraic Geom. 22 (2013), 141–174.Google Scholar
Zarhin, Yu. G., Endomorphisms of Abelian varieties over fields of finite characteristic, Izv. Akad. Nauk SSSR Ser. Mat. 39 (1975), 272–277.Google Scholar
Zucker, S., Generalized intermediate jacobians and the theorem on normal functions, Invent. Math. 33 (1976), 185–222.CrossRefGoogle Scholar
Zucker, S., The Hodge conjecture for cubic fourfolds, Composito Math. 34 (1977), 199–209.Google Scholar