Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-27T02:23:35.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois representations attached to moments of Kloosterman sums and conjectures of Evans

Part of: Exponential sums and character sums Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 October 2014

Zhiwei Yun  and
Christelle Vincent
Zhiwei Yun
Affiliation:
Department of Mathematics, Stanford University, 450 Serra Mall, Building 380, Stanford, CA 94305, USA email [email protected]
Christelle Vincent
Affiliation:
Department of Mathematics, Stanford University, 450 Serra Mall, Building 380, Stanford, CA 94305, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kloosterman sums for a finite field 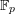$\mathbb{F}_{p}$ arise as Frobenius trace functions of certain local systems defined over 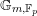$\mathbb{G}_{m,\mathbb{F}_{p}}$. The moments of Kloosterman sums calculate the Frobenius traces on the cohomology of tensor powers (or symmetric powers, exterior powers, etc.) of these local systems. We show that when 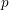$p$ ranges over all primes, the moments of the corresponding Kloosterman sums for 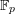$\mathbb{F}_{p}$ arise as Frobenius traces on a continuous 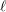$\ell$-adic representation of 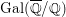$\text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$ that comes from geometry. We also give bounds on the ramification of these Galois representations. All of this is done in the generality of Kloosterman sheaves attached to reductive groups introduced by Heinloth, Ngô and Yun [Ann. of Math. (2) 177 (2013), 241–310]. As an application, we give proofs of conjectures of Evans [Proc. Amer. Math. Soc. 138 (2010), 517–531; Israel J. Math. 175 (2010), 349–362] expressing the seventh and eighth symmetric power moments of the classical Kloosterman sum in terms of Fourier coefficients of explicit modular forms. The proof for the eighth symmetric power moment conjecture relies on the computation done in Appendix B by C. Vincent.

Keywords

Kloosterman sumsGalois representationsmodularity

MSC classification

Primary: 11L05: Gauss and Kloosterman sums; generalizations
Secondary: 11F30: Fourier coefficients of automorphic forms 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 1 , January 2015 , pp. 68 - 120
Copyright
© The Author(s) 2014 

References

Arkhipov, S. and Bezrukavnikov, R., Perverse sheaves on affine flags and Langlands dual group (with an appendix by R. Bezrukavnikov and I. Mirković), Israel J. Math. 170 (2009), 135–183.Google Scholar
Beilinson, A., Bernstein, J. and Deligne, P., Faisceaux pervers, in Analysis and topology on singular spaces, I, Astérisque, vol. 100 (Société Mathématique de France, Paris, 1982), 5–171.Google Scholar
Berger, L., Li, H. and Zhu, H., Construction of some families of 2-dimensional crystalline representations, Math. Ann. 329 (2004), 365–377.CrossRefGoogle Scholar
Choi, H. T. and Evans, R., Congruences for sums of powers of Kloosterman sums, Int. J. Number Theory 3 (2007), 105–117.Google Scholar
Conrad, B., Lifting global representations with local properties, Preprint available at http://math.stanford.edu/∼conrad/.Google Scholar
Deligne, P., Théorie de Hodge. III, Publ. Math. Inst. Hautes Études Sci. (1974), 5–77.Google Scholar
Deligne, P., Applications de la formule des traces aux sommes trigonométriques, in Cohomologie étale. SGA 412, Lecture Notes in Mathematics, vol. 569 (Springer, New York, 1977).Google Scholar
Deligne, P., La conjecture de Weil, II, Publ. Math. Inst. Hautes Études Sci. (1980), 137–252.Google Scholar
Evans, R., Hypergeometric 3F 2(1∕4) evaluations over finite fields and Hecke eigenforms, Proc. Amer. Math. Soc. 138 (2010), 517–531.Google Scholar
Evans, R., Seventh power moments of Kloosterman sums, Israel J. Math. 175 (2010), 349–362.Google Scholar
Faltings, G., Almost étale extensions, in Cohomologies p-adiques et applications arithmétiques, II, Astérisque, vol. 279 (Société Mathématique de France, Paris, 2002), 185–270.Google Scholar
Fontaine, J.-M. and Laffaille, G., Construction de représentations p-adiques, Ann. Sci. Éc. Norm. Supér. (4) 15 (1982), 547–608.CrossRefGoogle Scholar
Frenkel, E. and Gross, B., A rigid irregular connection on the projective line, Ann. of Math. (2) 170 (2009), 1469–1512.Google Scholar
Fu, L. and Wan, D., L-functions for symmetric products of Kloosterman sums, J. Reine Angew. Math. 589 (2005), 79–103.Google Scholar
Fu, L. and Wan, D., L-functions of symmetric products of the Kloosterman sheaf over ℤ, Math. Ann. 342 (2008), 387–404.Google Scholar
Fu, L. and Wan, D., Functional equations of L-functions for symmetric products of the Kloosterman sheaf, Trans. Amer. Math. Soc. 362 (2010), 5947–5965.Google Scholar
Ginzburg, V., Perverse sheaves on a Loop group and Langlands duality, Preprint (1995), arXiv:math/9511007.Google Scholar
Gross, B. and Reeder, M., Arithmetic invariants of discrete Langlands parameters, Duke Math. J. 154 (2010), 431–508.CrossRefGoogle Scholar
Heinloth, J., Ngô, B.-C. and Yun, Z., Kloosterman sheaves for reductive groups, Ann. of Math. (2) 177 (2013), 241–310.Google Scholar
Hulek, K., Spandaw, J., van Geemen, B. and van Straten, D., The modularity of the Barth–Nieto quintic and its relatives, Adv. Geom. 1 (2001), 263–289.CrossRefGoogle Scholar
Katz, N., Gauss sums, Kloosterman sums and monodromy groups, Annals of Mathematics Studies, vol. 116 (Princeton University Press, Princeton, NJ, 1988).Google Scholar
Khare, C. and Wintenberger, J.-P., Serres modularity conjecture (I), Invent. Math. 178 (2009), 485–504.Google Scholar
Khare, C. and Wintenberger, J.-P., Serres modularity conjecture (II), Invent. Math. 178 (2009), 505–586.Google Scholar
Kisin, M., Potential semi-stability of p-adic étale cohomology, Israel J. Math. 129 (2002), 157–173.CrossRefGoogle Scholar
Kisin, M., Modularity of 2-dimensional Galois representations, in Current Developments in Mathematics (International Press, Somerville, MA, 2007), 191–230.Google Scholar
Laumon, G., Transformation de Fourier homogène, Bull. Soc. Math. France 131 (2003), 527–551.Google Scholar
Livné, R., Motivic orthogonal two-dimensional representations of Gal(ℚ∕ℚ), Israel J. Math. 92 (1995), 149–156.Google Scholar
Lusztig, G., Singularities, character formulas, and a q-analog of weight multiplicities, in Analysis and topology on singular spaces, II, III, Astérisque, vol. 101–102 (Société Mathématique de France, Paris, 1983), 208–229.Google Scholar
Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Ann. of Math. (2) 166 (2007), 95–143.CrossRefGoogle Scholar
Pappas, G. and Zhu, X., Local models of Shimura varieties and a conjecture of Kottwitz, Invent. Math. 194 (2013), 147–254.Google Scholar
Patrikis, S., Variations on a theorem of Tate, Preprint (2012), arXiv:1207.6724.Google Scholar
Peters, C., Top, J. and van der Vlugt, M., The Hasse zeta function of a K3 surface related to the number of words of weight 5 in the Melas codes, J. Reine Angew. Math. 432 (1992), 151–176.Google Scholar
Serre, J.-P., Corps Locaux, Publications de l’Université de Nancago, vol. VIII, second edition (Hermann, Paris, 1968).Google Scholar
Serre, J.-P., Sur les représentations modulaires de degré 2 de Gal(ℚ∕ℚ), Duke Math. J. 54 (1987), 179–230.Google Scholar
Serre, J.-P., Abelian l-adic representations and elliptic curves, Advanced book classics (Addison-Wesley, Redwood City, CA, 1989).Google Scholar