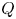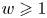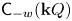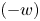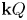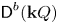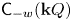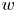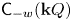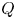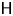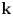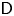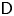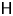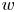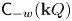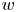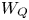Introduction
Cluster-tilting theory was introduced in [Reference Buan, Marsh, Reineke, Reiten and TodorovBMRRT06] as an approach to categorifying the cluster algebras of Fomin and Zelevinsky in [Reference Fomin and ZelevinskyFZ02]. Since its inception, cluster-tilting theory has gone on to have widespread connections with many areas of mathematics.
Classical cluster-tilting theory takes place in an 
$m$-cluster category 
$\mathsf {C}_m({\mathbf {k}} Q)$, for 
$m \geqslant 2$, which is an 
$m$-Calabi–Yau orbit category of the bounded derived category, 
$\mathsf {D}^b({\mathbf {k}} Q)$, of the path algebra of a finite acyclic quiver 
$Q$, where 
${\mathbf {k}}$ is an algebraically closed field. One of the most fruitful connections has been between the representation theory of finite-dimensional algebras and Coxeter combinatorics. For example, let 
$W$ be the Weyl group of type 
$Q$. There are natural bijections between the sets of clusters and noncrossing partitions associated to 
$W$; see [Reference Athanasiadis, Brady, McCammond and WattABMW06, Reference ReadingRea07, Reference Stump, Thomas and WilliamsSTW15]. There is, in turn, a bijection between the sets of clusters and cluster-tilting objects in the corresponding cluster category [Reference Buan, Reiten and ThomasBRT12]. Beyond cluster-tilting theory, there are many further connections between the combinatorics of noncrossing partitions and representation theory, e.g. in the classification of wide subcategories and torsion theories [Reference Ingalls and ThomasIT09], thick subcategories [Reference KöhlerKöh10] and Cartan lattices [Reference Hubery and KrauseHK16], to name a few. For a broad treatment of the combinatorics of noncrossing partitions in finite type, we refer the reader to [Reference Stump, Thomas and WilliamsSTW15].
Recently, there has been increasing interest in negative Calabi–Yau triangulated categories; see, for example, [Reference BrightbillBri21, Reference BrightbillBri20, Reference Coelho SimõesCoe12, Reference Coelho SimõesCoe15, Reference Coelho SimõesCoe17, Reference Coelho Simões and PauksztelloCP16, Reference Coelho Simões and PauksztelloCP20, Reference DugasDug15, Reference Holm, Jørgensen and YangHJY13, Reference Iyama and JinIJ20, Reference JinJin20, Reference JinJin19, Reference Koenig and LiuKL12]. For an integer 
$w \geqslant 1$ and an acyclic quiver 
$Q$ there is an orbit category 
$\mathsf {C}_{-w}({\mathbf {k}} Q)$ of the bounded derived category 
$\mathsf {D}^b({\mathbf {k}} Q)$ which is 
$(-w)$-Calabi–Yau. This orbit category can be thought of as a ‘negative (Calabi–Yau) cluster category’. In this setting, the analogue of 
$m$-cluster-tilting objects are so-called 
$w$-simple-minded systems. Evidence supporting the viewpoint that 
$w$-simple-minded systems are a negative Calabi–Yau analogue of cluster-tilting objects is advanced by a growing body of work [Reference Buan, Reiten and ThomasBRT12, Reference Coelho SimõesCoe12, Reference Coelho SimõesCoe15, Reference Coelho SimõesCoe17, Reference Coelho Simões and PauksztelloCP20, Reference DugasDug15, Reference Iyama and JinIJ20, Reference JinJin20, Reference JinJin19].
It is therefore natural to ask about connections between negative cluster categories and Coxeter combinatorics. Previous work in this direction includes [Reference Buan, Reiten and ThomasBRT12, Reference Coelho SimõesCoe12, Reference Iyama and JinIJ20, Reference Stump, Thomas and WilliamsSTW15]. Again let 
$Q$ be an acyclic quiver with corresponding Weyl group 
$W$. In [Reference Coelho SimõesCoe12], the first author established a bijection between so-called positive noncrossing partitions of 
$W$ and (
$1$-)simple-minded systems in 
$\mathsf {C}_{-1}({\mathbf {k}} Q)$ when 
$Q$ is Dynkin. In [Reference Buan, Reiten and ThomasBRT12], Buan, Reiten and Thomas obtained a bijection between simple-minded collections lying inside some ‘fundamental domain’ and 
$w$-noncrossing partitions, which was a forefather of the König–Yang correspondences [Reference Koenig and YangKY14]. Most recently, in [Reference Iyama and JinIJ20], Iyama and Jin generalised [Reference Buan, Reiten and ThomasBRT12] and [Reference Coelho SimõesCoe12] to obtain a bijection between 
$w$-simple-minded systems in 
$\mathsf {C}_{-w}({\mathbf {k}} Q)$ and positive 
$w$-noncrossing partitions, again for 
$Q$ Dynkin. This bijection proceeds via a bijection between 
$w$-simple-minded systems in 
$\mathsf {C}_{-w}({\mathbf {k}} Q)$ and simple-minded collections lying in the fundamental domain 
$\mathcal {F}_{-w}$ (see § 1.2 for the precise definition) of 
$\mathsf {D}^b({\mathbf {k}} Q)$; see [Reference Iyama and JinIJ20, Theorem 1.2].
In this article, we extend this bijection to the case that 
$Q$ is an arbitrary quiver in the following main theorem.
Theorem A Theorem 4.1
Let 
$Q$ be an acyclic quiver. The natural projection functor 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}({\mathbf {k}} Q)$ induces a bijection
\[\Big\{\begin{matrix}\textrm{simple-minded collections of }\, \mathsf{D}^b({\mathbf{k}} Q)\\ \textrm{contained in}\, \mathcal{F}_{{-}w}\end{matrix}\Big\} \stackrel{1-1}{\longleftrightarrow} \Big\{\begin{matrix} w\textrm{-simple-minded systems}\\ \textrm{in }\mathsf{C}_{{-}w}\end{matrix}\Big\}. \] Using Theorem A, we are then able to obtain the following bijection involving noncrossing partitions for any acyclic quiver 
$Q$.
Theorem B Theorem 6.4
Let 
$Q$ be an acyclic quiver. There is a bijection
\[ \Big\{ \begin{matrix} \textrm{positive }w\textrm{-noncrossing}\\ \textrm{partitions of}\ W_Q\end{matrix} \Big\} \stackrel{1-1}{\longleftrightarrow} \Big\{\begin{matrix} w\textrm{-simple-minded systems}\\ \textrm{in }\mathsf{C}_{{-}w}({\mathbf{k}} Q)\end{matrix}\Big\}. \] In order to obtain Theorem A, we require another observation that we believe holds independent interest and will be widely applicable. Let 
$\mathsf {D}$ be a Hom-finite, Krull–Schmidt, 
${\mathbf {k}}$-linear triangulated category and suppose that 
$\mathsf {H} \subseteq \mathsf {D}$ is the heart of a bounded t-structure. One can ask what is the relationship between the following properties of 
$\mathsf {H}$:
•
$\mathsf {H}$ is a length category with finitely many simple objects;•
$\mathsf {H}$ has enough injective objects and enough projective objects; and•
$\mathsf {H}$ is a functorially finite subcategory of $\mathsf {D}$.
Of these three properties, the final property is the odd one out: it is the only property which takes the ambient triangulated category in which 
$\mathsf {H}$ sits into account. As such a relationship between these properties is potentially very powerful. Unfortunately, Example 2.13 shows that there is no relationship, in general, between the first and the third properties. However, our third main theorem provides a relationship between the second and third properties of 
$\mathsf {H}$. It is this relationship which is a crucial ingredient in our proof of Theorem A.
Theorem C Corollary 2.8
Let 
$\mathsf {D}$ be a Hom-finite, Krull–Schmidt, saturated triangulated category. Suppose 
$\mathsf {H} \subseteq \mathsf {D}$ is the heart of a bounded t-structure. Then 
$\mathsf {H}$ is functorially finite in 
$\mathsf {D}$ if and only if 
$\mathsf {H}$ has enough injectives and enough projectives.
In this statement, we have specialised to the case that 
$\mathsf {D}$ is a saturated triangulated category, for example, 
$\mathsf {D} = \mathsf {D}^b(A)$ for a finite-dimensional 
${\mathbf {k}}$-algebra 
$A$ of finite global dimension or 
$\mathsf {D} = \mathsf {D}^b(\mathsf {coh}(X))$ for a smooth projective variety 
$X$. A more general, technical statement without the saturated hypothesis is proved in Theorem 2.4.
We briefly sketch the structure of the paper. In § 1, we recall the basic concepts we use in the paper. In § 2 we prove Theorem C. Section 3 recalls the basic properties of orthogonal collections, simple-minded systems and simple-minded collections, and establishes a characterisation of simple-minded collections in terms of Riedtmann configurations that may be more widely applicable and illustrates the parallel between simple-minded collections and simple-minded systems. In § 4, we prove our main theorem, Theorem A. Section 5 establishes a bijection between 
$w$-simple-minded systems and certain sincere orthogonal collections which is the crucial tool to pass from Theorem A to Theorem B, which is done in § 6. Finally, the paper includes an appendix by the first two authors and Alexandra Zvonareva in which we give an alternative proof of a theorem by Jin [Reference JinJin19] on the reduction of simple-minded collections using the characterisation in terms of Riedtmann configurations, which avoids the passage to a Verdier localisation, and is more in the spirit of [Reference Coelho Simões and PauksztelloCP20].
Notation convention
In abstract abelian and triangulated categories we use lowercase Roman letters to denote objects. When we specialise to module categories or derived categories of an algebra, we use uppercase letters to denote objects. The philosophy behind this is that in the latter case, these objects have elements.
1. Preliminaries
To begin with 
$\mathsf {D}$ is a Hom-finite, Krull–Schmidt, 
${\mathbf {k}}$-linear triangulated category over a field 
${\mathbf {k}}$, where Hom-finite means that 
$\mathsf {Hom}_\mathsf {D}(x,y)$ is finite-dimensional as a 
${\mathbf {k}}$-vector space for any objects 
$x$ and 
$y$ in 
$\mathsf {D}$. Starting from § 3, 
${\mathbf {k}}$ is assumed to be algebraically closed. The shift or suspension functor is denoted by 
$\Sigma \colon \mathsf {D} \to \mathsf {D}$. Later, we specialise to the case that 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$ for a finite acyclic quiver 
$Q$. Abusing notation, if 
$\mathsf {X}$ is a collection of objects of 
$\mathsf {D}$ and 
$d$ is an object of 
$\mathsf {D}$ we write 
$\mathsf {Hom}_\mathsf {D}(\mathsf {X},d)$ to mean 
$\mathsf {Hom}_\mathsf {D}(x,d)$ where we take each 
$x \in \mathsf {X}$ in turn; likewise for 
$\mathsf {Hom}_\mathsf {D}(d,\mathsf {X})$. We assume all subcategories are full and strict.
For subcategories 
$\mathsf {X}$ and 
$\mathsf {Y}$ of 
$\mathsf {D}$, we write
\[ \mathsf{X} * \mathsf{Y} = \{ d \in \mathsf{D} \mid \text{there exists a triangle } x\rightarrow d\rightarrow y\rightarrow \Sigma x \text{ with } x \in \mathsf{X} \text{ and } y \in \mathsf{Y}\}. \]
We note that by the octahedral axiom, the 
$*$ product of subcategories is associative. A subcategory 
$\mathsf {X}$ is extension-closed if 
$\mathsf {X} * \mathsf {X} = \mathsf {X}$. We denote by 
$\langle \mathsf {X} \rangle$, or sometimes by 
$\langle \mathsf {X} \rangle _\mathsf {D}$ when we need to emphasise the triangulated category in which we are working, the extension closure of 
$\mathsf {X}$, that is, the smallest extension-closed subcategory of 
$\mathsf {D}$ containing 
$\mathsf {X}$. The right and left perpendicular categories of 
$\mathsf {X}$ are defined as follows:
\[ \mathsf{X}^\perp{=} \{ d \in \mathsf{D} \mid \mathsf{Hom}(\mathsf{X},d) = 0 \} \text{ and } {}^\perp \mathsf{X} = \{ d \in \mathsf{D} \mid \mathsf{Hom}(d,\mathsf{X}) = 0 \}. \]In § 5 we also require a notion of perpendicular category that is more suited to abelian categories; see Definition 5.6.
An autoequivalence 
$\mathbb {S} \colon \mathsf {D} \to \mathsf {D}$ is called a Serre functor if for each 
$x,y \in \mathsf {D}$ there is an isomorphism,
\[ \mathsf{Hom}(x,y) \simeq D\,\mathsf{Hom}(y, \mathbb{S} x), \]
which is natural in 
$x$ and 
$y$, where 
$D = \mathsf {Hom}_{\mathbf {k}}(-,{\mathbf {k}})$. If 
$\mathsf {D}$ has a Serre functor, it is unique up to isomorphism and we say 
$\mathsf {D}$ satisfies Serre duality. For details, we refer to [Reference Reiten and van den BerghRvdB02].
Let 
$w\in \mathbb {Z}$. A triangulated category 
$\mathsf {D}$ satisfying Serre duality is 
$w$-Calabi–Yau (or 
$w$-CY) if there is a natural isomorphism 
$\mathbb {S} \simeq \Sigma ^w$, where 
$\mathbb {S}$ is the Serre functor on 
$\mathsf {D}$.
1.1 Functorially finite subcategories and (co-)t-structures
Let 
$\mathsf {X}$ be a subcategory of 
$\mathsf {D}$, and 
$d$ an object in 
$\mathsf {D}$. A morphism 
$f \colon x \to d$, with 
$x \in \mathsf {X}$, is a right 
$\mathsf {X}$-approximation (or an 
$\mathsf {X}$-precover) of 
$d$ if 
$\mathsf {Hom}(\mathsf {X}, f) \colon \mathsf {Hom}(\mathsf {X},x) \to \mathsf {Hom}(\mathsf {X},d)$ is surjective. The morphism 
$f$ is called right minimal if any 
$g \colon x \to x$ satisfying 
$fg = f$ is an automorphism. The morphism 
$f$ is called a minimal right 
$\mathsf {X}$-approximation (or an 
$\mathsf {X}$-cover) of 
$d$ if it is a right 
$\mathsf {X}$-approximation of 
$d$ and is right minimal. If 
$f \colon x \to d$ is a minimal right 
$\mathsf {X}$-approximation and 
$h \colon x' \to d$ is a right 
$\mathsf {X}$-approximation, then 
$x$ is isomorphic to a direct summand of 
$x'$ (see, e.g., [Reference Auslander and SmaløAS80]).
If every object in 
$\mathsf {D}$ admits a right 
$\mathsf {X}$-approximation, then 
$\mathsf {X}$ is said to be contravariantly finite or precovering. If every object in 
$\mathsf {D}$ admits a minimal right 
$\mathsf {X}$-approximation, then 
$\mathsf {X}$ is said to be covering. There are dual notions of (minimal) left 
$\mathsf {X}$-approximations (or 
$\mathsf {X}$-pre-envelopes and 
$\mathsf {X}$-envelopes) and covariantly finite (or (pre-)enveloping) subcategories. The subcategory 
$\mathsf {X}$ of 
$\mathsf {D}$ is called functorially finite if it is both contravariantly finite and covariantly finite. We note that if 
$\mathsf {D}$ is Hom-finite and Krull–Schmidt then any precovering (respectively, pre-enveloping) subcategory is automatically covering (respectively, enveloping); see, e.g., [Reference Auslander and SmaløAS80].
Definition 1.1 A pair of full subcategories 
$(\mathsf {X},\mathsf {Y})$ of 
$\mathsf {D}$, each closed under summands, such that 
$\mathsf {Hom}_\mathsf {D}(\mathsf {X},\mathsf {Y}) = 0$ and 
$\mathsf {D} = \mathsf {X} * \mathsf {Y}$ is called a:
• t-structure if, in addition,
$\Sigma \mathsf {X} \subseteq \mathsf {X}$ (equivalently, $\Sigma ^{-1} \mathsf {Y} \subseteq \mathsf {Y}$); the heart of $(\mathsf {X},\mathsf {Y})$, $\mathsf {H} = \mathsf {X} \cap \Sigma \mathsf {Y}$, is an abelian category [Reference Beilinson, Bernstein and DeligneBBD82];• co-t-structure [Reference PauksztelloPau08] (or weight structure [Reference BondarkoBon10]) if, in addition,
$\Sigma ^{-1} \mathsf {X} \subseteq \mathsf {X}$ (equivalently, $\Sigma \mathsf {Y} \subseteq \mathsf {Y})$. Its coheart $\mathsf {S} = \Sigma \mathsf {X} \cap \mathsf {Y}$ is a presilting subcategory, i.e. $\mathsf {Hom}_\mathsf {D}(\mathsf {S},\Sigma ^{>0} \mathsf {S}) = 0$ (see, e.g., [Reference Aihara and IyamaAI12]).
A (co-)t-structure is bounded if 
$\mathsf {D} = \bigcup _{i \in \mathbb {Z}} \Sigma ^i \mathsf {X} = \bigcup _{i \in \mathbb {Z}} \Sigma ^i \mathsf {Y}$. A co-t-structure is bounded if and only if its coheart 
$\mathsf {S}$ is a silting subcategory, i.e. 
$\mathsf {S}$ is presilting and the thick subcategory of 
$\mathsf {D}$ generated by 
$\mathsf {S}$ is 
$\mathsf {D}$ (see [Reference Mendoza Hernández, Sáenz Valadez, Santiago Vargas and Souto SalorioMSSS13, Theorem 4.20]).
A co-t-structure 
$(\mathsf {U},\mathsf {V})$ is said to be left adjacent to a t-structure 
$(\mathsf {X},\mathsf {Y})$ if 
$\mathsf {V} = \mathsf {X}$ (see [Reference BondarkoBon10]). Analogously, 
$(\mathsf {U},\mathsf {V})$ is right adjacent to 
$(\mathsf {X},\mathsf {Y})$ if 
$\mathsf {U} = \mathsf {Y}$.
Note that for a t-structure 
$(\mathsf {X},\mathsf {Y})$, the inclusion 
$\mathsf {X} \to \mathsf {D}$ has a right adjoint and the inclusion 
$\mathsf {Y} \to \mathsf {D}$ has a left adjoint; these are given by the truncation functors. Therefore, the subcategory 
$\mathsf {X}$ is always contravariantly finite in 
$\mathsf {D}$ and the subcategory 
$\mathsf {Y}$ is always covariantly finite in 
$\mathsf {D}$, and the approximations are even functorial. In contrast, if 
$(\mathsf {U},\mathsf {V})$ is a co-t-structure in 
$\mathsf {D}$, then 
$\mathsf {U}$ is contravariantly finite in 
$\mathsf {D}$ and 
$\mathsf {V}$ is covariantly finite in 
$\mathsf {D}$, but these approximations need not be functorial.
We recall the following standard characterisation of bounded t-structures; see, for example, [Reference BridgelandBri07, Lemma 3.2].
Lemma 1.2 Let 
$(\mathsf {X},\mathsf {Y})$ be a t-structure in 
$\mathsf {D}$ with heart 
$\mathsf {H}$. The following conditions are equivalent:
(1) the t-structure
$(\mathsf {X},\mathsf {Y})$ is bounded;(2)
$\mathsf {X} = \bigcup _{n \geqslant 0} \Sigma ^n \mathsf {H} * \Sigma ^{n-1} \mathsf {H} * \cdots * \mathsf {H}$ and $\mathsf {Y} = \bigcup _{n <0} \Sigma ^{-1} \mathsf {H} * \Sigma ^{-2} \mathsf {H} * \cdots * \Sigma ^n \mathsf {H}$;(3)
$\mathsf {D} = \bigcup _{n \geqslant m} \Sigma ^n \mathsf {H} * \Sigma ^{n-1} \mathsf {H} * \cdots * \Sigma ^{m+1} \mathsf {H} * \Sigma ^m \mathsf {H}$.
Definition 1.3 A bounded t-structure 
$(\mathsf {X},\mathsf {Y})$ in 
$\mathsf {D}$ with heart 
$\mathsf {H}$ is called algebraic if 
$\mathsf {H}$ is a length category (every object has finite length, i.e. is Artinian as well as Noetherian) with only finitely many simple objects.
For example, the property of being algebraic holds for bounded t-structures whose hearts are module categories over finite-dimensional algebras.
1.2 Hereditary algebras and negative cluster categories
For this section, 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$ for some finite acyclic quiver 
$Q$. The main reference for the structure of derived categories of hereditary algebras (equivalently, path algebras of acyclic quivers) is [Reference HappelHap88].
Recall that an algebra 
$A$ is hereditary if it is of global dimension 
$0$ or 
$1$, i.e. if the bifunctors 
$\mathsf {Ext}^n_A(-,-)$ are zero for 
$n \geqslant 2$. Typical examples are the path algebras 
$A={\mathbf {k}} Q$. A well-known lemma says that each object of 
$\mathsf {D}^b({\mathbf {k}} Q)$ decomposes as a direct sum of its cohomology. In particular, its Auslander–Reiten (AR) quiver has the following form:
Morphisms go from left to right, and because for two modules 
$M, N \in \mathsf{mod}({{\mathbf {k}} Q})$, one has 
$\mathsf {Hom}_{\mathsf {D}^b({\mathbf {k}} Q)}(M,\Sigma ^n N) = \mathsf {Ext}^n_{{\mathbf {k}} Q}(M,N)$, nonzero morphisms exist only from one degree to the next and not any higher.
In this article, we are interested in a certain orbit category of 
$\mathsf {D}^b({\mathbf {k}} Q)$ which is constructed as follows; see [Reference Buan, Marsh, Reineke, Reiten and TodorovBMRRT06]. Let 
$w \geqslant 1$ and 
$F = \Sigma ^w \mathbb {S}$. We define the category
\[ \mathsf{C}_{{-}w} = \mathsf{C}_{{-}w}({\mathbf{k}} Q) \mathrel{\mathop:}= \mathsf{D}^b({\mathbf{k}} Q)/F, \]
with the same objects as 
$\mathsf {D}$ and whose morphisms are given by
\[ \mathsf{Hom}_{\mathsf{C}_{{-}w}}(x,y) = \bigoplus_{n \in \mathbb{Z}} \mathsf{Hom}_{\mathsf{D}^b({\mathbf{k}} Q)}(x, F^n y). \]
We write 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}$ for the natural projection functor. The orbit category 
$\mathsf {C}_{-w}$ is a triangulated category (see [Reference KellerKel05]) which is 
$(-w)$-Calabi–Yau; this uses that the algebra 
${\mathbf {k}} Q$ is hereditary. Compare 
$\mathsf {C}_{-w}$ with the construction of the 
$m$-cluster category, 
$\mathsf {D}^b({\mathbf {k}} Q)/\Sigma ^{-m}\mathbb {S}$, for 
$m \geqslant 2$, which is an 
$m$-Calabi–Yau triangulated category. As such, we refer to 
$\mathsf {C}_{-w}$ as a negative cluster category or a 
$(-w)$-cluster category.
It is often convenient to compute inside 
$\mathsf {C}_{-w}$ using a so-called fundamental domain in 
$\mathsf {D}^b({\mathbf {k}} Q)$. Let 
$(\mathsf {X},\mathsf {Y})$ be the standard t-structure in 
$\mathsf {D}^b({\mathbf {k}} Q)$, i.e. the t-structure with 
$\mathsf {X} = \mathsf {D}^{\geqslant 0}({\mathbf {k}} Q), \mathsf {Y} = \mathsf {D}^{<0}({\mathbf {k}} Q)$ and heart 
$\mathsf {H} = \mathsf{mod}({{\mathbf {k}} Q})$. We define the fundamental domain of 
$\mathsf {C}_{-w}$ to be
\[ \mathcal{F}_{{-}w} \mathrel{\mathop:}= \mathsf{X} \cap \Sigma^w \mathbb{S} \mathsf{Y}. \]
The natural projection functor 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}$ induces a bijection
\[ \{\text{indecomposable objects in } \mathcal{F}_{{-}w}\} \stackrel{1-1}{\longleftrightarrow} \{\text{indecomposable objects of } \mathsf{C}_{{-}w}\}. \]
The following is a schematic of the fundamental domain 
$\mathcal {F}_{-w}$ inside 
$\mathsf {D}^b({\mathbf {k}} Q)$,
where the shaded grey region on the right-hand side comprises 
$\Sigma ^w \mathsf {inj}({\mathbf {k}} Q)$, where 
$\mathsf {inj}({\mathbf {k}} Q)$ denotes the full subcategory of injective 
${\mathbf {k}} Q$-modules.
Finally, working inside 
$\mathcal {F}_{-w}$ allows us to compute Hom spaces easily.
Lemma 1.4 [Reference Iyama and JinIJ20, Lemma 3.4]
Suppose 
$x,y \in \mathcal {F}_{-w}$ and 
$0 \leqslant i \leqslant w$. Then
\[ \mathsf{Hom}_{\mathsf{C}_{{-}w}}(x,\Sigma^{{-}i} y) = \mathsf{Hom}_{\mathsf{D}^b({\mathbf{k}} Q)}(x,\Sigma^{{-}i}y) \oplus D\,\mathsf{Hom}_{\mathsf{D}^b({\mathbf{k}} Q)}(y, \Sigma^{i-w} x). \]2. Functorially finite hearts
In this section, we establish an unexpected characterisation of algebraic t-structures: our third main theorem, which we state and prove first, relates homological properties of hearts to approximation properties. The theorem extends a characterisation of Bondarko in terms of co-t-structures; see [Reference BondarkoBon19, Theorem 5.3.1].
In this section, 
$\mathsf {D}$ will be a Hom-finite, Krull–Schmidt triangulated category. We start by giving two definitions following [Reference Assem, Souto Salorio and TrepodeAST08] and [Reference Nicolás, Saorín and ZvonarevaNSZ19].
Definition 2.1 Let 
$(\mathsf {X},\mathsf {Y})$ be a t-structure in 
$\mathsf {D}$. The projective coheart of 
$(\mathsf {X},\mathsf {Y})$ is 
$\mathsf {S} = {}^\perp \Sigma \mathsf {X} \cap \mathsf {X}$ and the injective coheart of 
$(\mathsf {X},\mathsf {Y})$ is 
$\mathsf {C} = \mathsf {Y}^\perp \cap \Sigma \mathsf {Y}$.
As in [Reference Nicolás, Saorín and ZvonarevaNSZ19], we do not require the existence of a co-t-structure adjacent to 
$(\mathsf {X},\mathsf {Y})$ in order to consider the projective or injective cohearts. The projective and injective cohearts were also considered in [Reference Assem, Souto Salorio and TrepodeAST08], where the objects of the projective and injective cohearts are called the ‘Ext-projectives of the aisle 
$\mathsf {X}$’ and the ‘Ext-injectives of the coaisle 
$\Sigma \mathsf {Y}$’, respectively. This terminology inspires the next definition.
Definition 2.2 Let 
$(\mathsf {X},\mathsf {Y})$ be a t-structure in 
$\mathsf {D}$ with heart 
$\mathsf {H} = \mathsf {X} \cap \Sigma \mathsf {Y}$. We say that 
$(\mathsf {X},\mathsf {Y})$ has enough Ext-projectives if 
$\mathsf {S}$ is contravariantly finite in 
$\mathsf {X}$ and 
$\mathsf {S}^\perp \cap \mathsf {H} = 0$. Similarly, we say 
$(\mathsf {X},\mathsf {Y})$ has enough Ext-injectives if 
$\mathsf {C}$ is covariantly finite in 
$\Sigma \mathsf {Y}$ and 
${}^\perp \mathsf {C} \cap \mathsf {H} = 0$.
Remark 2.3 The projective coheart 
$\mathsf {S}$ and injective coheart 
$\mathsf {C}$ of a t-structure 
$(\mathsf {X},\mathsf {Y})$ satisfy 
$\mathsf {Hom}(\mathsf {S}, \Sigma ^{>0} \mathsf {S}) = 0$ and 
$\mathsf {Hom}(\mathsf {C}, \Sigma ^{>0} \mathsf {C}) = 0$; that is, they are examples of presilting subcategories. In most examples we have in mind, the presilting subcategories have an additive generator and therefore are automatically functorially finite, so the hypotheses that 
$\mathsf {S}$ is contravariantly finite in 
$\mathsf {D}$ and 
$\mathsf {C}$ is covariantly finite in 
$\mathsf {D}$ are quite mild.
Theorem 2.4 Let 
$\mathsf {D}$ be a Hom-finite, Krull–Schmidt, 
${\mathbf {k}}$-linear triangulated category. Let 
$(\mathsf {X},\mathsf {Y})$ be a bounded t-structure in 
$\mathsf {D}$ with heart 
$\mathsf {H} = \mathsf {X} \cap \Sigma \mathsf {Y}$, projective coheart 
$\mathsf {S} = {}^\perp \Sigma \mathsf {X} \cap \mathsf {X}$ and injective coheart 
$\mathsf {C} = \mathsf {Y}^\perp \cap \Sigma \mathsf {Y}$. The following are equivalent:
(1)
$\mathsf {H}$ is contravariantly finite (respectively, covariantly finite) in $\mathsf {D}$ and $(\mathsf {X},\mathsf {Y})$ has enough Ext-injectives (respectively, Ext-projectives);(2)
$\mathsf {H}$ has enough injectives (respectively, projectives) and each injective object $e \in \mathsf {H}$ admits an $\mathsf {H}$-monomorphism $e \hookrightarrow H^0(c)$ for some $c \in \mathsf {C}$ (respectively, each projective object $p \in \mathsf {H}$ admits an $\mathsf {H}$-epimorphism $H^0(s) \twoheadrightarrow p$ for some $s \in \mathsf {S}$);(3)
$(\mathsf {X},\mathsf {Y})$ has a right (respectively, left) adjacent co-t-structure.
The characterisation 
$(2) \Longleftrightarrow (3)$ was observed in [Reference BondarkoBon19, Theorem 5.3.1]; we provide details of the argument for 
$(2) \Longrightarrow (3)$ for the convenience of the reader. We only prove the unbracketed statements; the bracketed statements are dual.
Proof. First, we prove 
$(1) \Longrightarrow (2)$. Suppose 
$\mathsf {H}$ is contravariantly finite in 
$\mathsf {D}$. We must show that every object of 
$\mathsf {H}$ admits an injective envelope. Let 
$h \in \mathsf {H}$ and take a minimal right 
$\mathsf {H}$-approximation of 
$\Sigma h$:
\[ h' \to \Sigma h \to \Sigma e \to \Sigma h'. \]
By the triangulated Wakamatsu lemma 
$\Sigma e \in \mathsf {H}^\perp$ (see, e.g., [Reference JørgensenJør09, Lemma 2.1]; this is where the hypotheses that 
$\mathsf {D}$ is Hom-finite and Krull–Schmidt are used). Rotating this triangle gives us the triangle 
$h \to e \to h' \to \Sigma h$, whence extension closure of 
$\mathsf {H}$ means that 
$e \in \mathsf {H}$. Thus, 
$e \in \mathsf {H} \cap (\Sigma ^{-1} \mathsf {H})^\perp$, i.e. 
$\mathsf {Ext}^1_\mathsf {H}(-,e) = 0$ and 
$e$ is injective. However, each short exact sequence 
$0 \to h_1 \to h_2 \to h_3 \to 0$ in 
$\mathsf {H}$ corresponds to a distinguished triangle 
$h_1 \to h_2 \to h_3 \to \Sigma h_1$ and vice versa so that we have a short exact sequence 
$0 \to h \to e \to h' \to 0$, in which case 
$h \hookrightarrow e$ is an injective envelope.
Now suppose 
$e \neq 0$ is an injective object of 
$\mathsf {H}$. As 
$(\mathsf {X},\mathsf {Y})$ has enough Ext-injectives, we can take a (minimal) left 
$\mathsf {C}$-approximation of 
$e$ and extend it to a distinguished triangle
\[ z \to e \to c \to \Sigma z. \]
We claim that 
$z \in \mathsf {Y}$. As 
$e \neq 0$ and 
${}^\perp \mathsf {C} \cap \mathsf {H} = 0$, we have that 
$c \neq 0$ and the Wakamatsu lemma tells us that 
$z \in {}^\perp \mathsf {C}$. We also see that 
$z \in \Sigma \mathsf {Y}$ because 
$e \in \mathsf {X} \cap \Sigma \mathsf {Y}$, 
$\Sigma ^{-1} c \in \Sigma ^{-1} \mathsf {C} \subseteq \mathsf {Y} \subseteq \Sigma \mathsf {Y}$ and 
$\Sigma \mathsf {Y}$ is extension closed. Truncating 
$z$ with respect to 
$(\mathsf {X},\mathsf {Y})$ gives a triangle,
\[ h_z \to z \to y_z \to \Sigma h_z, \]
with 
$h_z \in \mathsf {H}$. Applying 
$\mathsf {Hom}(-,\mathsf {C})$ to this triangle and using 
$\mathsf {Hom}(\Sigma ^{-1}\mathsf {Y},\mathsf {C})\subseteq \mathsf {Hom}(\mathsf {Y},\mathsf {C})=0$ reveals that 
$h_z \in {}^\perp \mathsf {C} \cap \mathsf {H} = 0$. Hence, 
$z \simeq y_z \in \mathsf {Y}$, as claimed.
Finally, consider the truncation triangle of 
$c$ with respect to 
$(\mathsf {X},\mathsf {Y})$:
\[ h_c \to c \to y_c \to \Sigma h_c, \]
noting that 
$h_c \in \mathsf {H}$, that is, 
$H^0(c) = h_c$. As 
$e \in \mathsf {X}$, the composition 
$e \to c \to y_c$ is zero, which means we obtain the following octahedral diagram.
From the left-hand vertical triangle we read off that 
$h \in \mathsf {X}$ and from the lower horizontal triangle we read off that 
$h \in \Sigma \mathsf {Y}$, using 
$z\in \mathsf {Y}$. Hence, 
$h \in \mathsf {H}$, meaning that the triangle 
$e \to h_c \to h \to \Sigma e$ corresponds to a short exact sequence 
$0 \to e \to h_c \to h \to 0$ in 
$\mathsf {H}$. Hence, the injective object 
$e \in \mathsf {H}$ admits an 
$\mathsf {H}$-monomorphism 
$e \hookrightarrow H^0(c)$ for some 
$c \in \mathsf {C}$.
$(2) \Longrightarrow (3)$. Let 
$\mathsf {U} = \mathsf {Y}$ and 
$\mathsf {V} = \mathsf {Y}^\perp$, we need to show that 
$(\mathsf {U},\mathsf {V})$ is a co-t-structure in 
$\mathsf {D}$. Hom-vanishing 
$\mathsf {Hom}(\mathsf {U}, \mathsf {V}) = 0$ is immediate; closure under direct summands and closure under shifts are clear because 
$\mathsf {U} = \mathsf {Y}$ is the co-aisle of a t-structure. Hence, we only need to exhibit for each 
$d \in \mathsf {D}$ the approximation triangle 
$u \to d \to v \to \Sigma u$ with 
$u \in \mathsf {U}$ and 
$v \in \mathsf {V}$. As 
$(\mathsf {X},\mathsf {Y})$ is bounded, for each 
$d \in \mathsf {D}$ there exists 
$n \in \mathbb {Z}$ such that 
$d \in \Sigma ^n \mathsf {Y} = \Sigma ^n \mathsf {U}$. Hence, if 
$n \leqslant 0$, we have 
$d \in \mathsf {Y}$ and the trivial triangle 
$d \stackrel {1}{\longrightarrow } d \longrightarrow 0 \longrightarrow \Sigma d$ suffices. Thus, we assume 
$n > 0$ and proceed by induction on 
$n$.
Suppose 
$n = 1$, i.e. 
$d \in \Sigma \mathsf {Y}$ and consider its 
$(\mathsf {X},\mathsf {Y})$-truncation triangle,
\[ h_d \to d \to y_d \to \Sigma h_d, \]
noting that 
$h_d \in \mathsf {X} \cap \Sigma \mathsf {Y} = \mathsf {H}$. As 
$\mathsf {H}$ has enough injectives, there exists an injective envelope 
$h_d \hookrightarrow e$, i.e. 
$e \in \mathsf {H}$ injective. By hypothesis, there exists an 
$\mathsf {H}$-monomorphism 
$e \hookrightarrow h_c$, where 
$h_c = H^0(c)$ for some 
$c \in \mathsf {C}$, the injective coheart. Let 
$h'' \in \mathsf {H}$ be the cokernel of the composition of these two morphisms: 
$0 \to h_d \to h_c \to h'' \to 0$.
As 
$\mathsf {Hom}(\Sigma ^{-1} y_d, c) = 0$ due to 
$\Sigma ^{-1} \mathsf {Y} \subseteq \mathsf {Y}$ and 
$\mathsf {C} \subseteq \mathsf {Y}^\perp$, the morphism 
$h_d \to h_c$ gives rise to a commutative diagram of triangles,
which, by [Reference Beilinson, Bernstein and DeligneBBD82, Proposition 1.1.11], extends to the following 
$3 \times 3$ diagram.
From the right-hand vertical triangle, we read off 
$y \in \mathsf {Y}$ and the top-most horizontal triangle gives 
$u \in \mathsf {U} = \mathsf {Y}$, using 
$\Sigma ^{-1} h'' \in \Sigma ^{-1} \mathsf {H} \subseteq \mathsf {Y}$. As 
$c \in \mathsf {C} = \mathsf {Y}^\perp \cap \Sigma \mathsf {Y} = \mathsf {V} \cap \Sigma \mathsf {U} \subseteq \mathsf {V}$, we see that 
$u \to d \to c \to \Sigma u$ is a 
$(\mathsf {U},\mathsf {V})$-approximation triangle of 
$d$.
Now suppose 
$d \in \Sigma ^n \mathsf {Y}$ for some 
$n > 1$. By induction, there is a 
$(\mathsf {U},\mathsf {V})$-approximation triangle 
$u_1 \to \Sigma ^{-1} d \to v_1 \to \Sigma u_1$ with 
$u_1 \in \mathsf {U}$ and 
$v_1 \in \mathsf {V}$. By the base step of the induction, there is a 
$(\mathsf {U},\mathsf {V})$-approximation triangle 
$u \to \Sigma u_1 \to c \to \Sigma u$ with 
$u \in \mathsf {U}$ and 
$c \in \mathsf {C}$. Applying the octahedral axiom, we obtain the following commutative diagram,
in which 
$v \in \mathsf {V}$ because 
$c \in \mathsf {C} \subseteq \mathsf {V}$ and 
$\Sigma \mathsf {V} \subseteq \mathsf {V}$. Hence, 
$u \to d \to v \to \Sigma u$ provides the required 
$(\mathsf {U},\mathsf {V})$-approximation triangle of 
$d$. Hence, the t-structure 
$(\mathsf {X},\mathsf {Y})$ has a right adjacent co-t-structure.
$(3) \Longrightarrow (1)$. As there is a right adjacent co-t-structure, it follows that 
$\Sigma \mathsf {Y}$ is contravariantly finite in 
$\mathsf {D}$. Thus, to obtain that 
$\mathsf {H}$ is contravariantly finite in 
$\mathsf {D}$ it is enough to show that 
$\mathsf {H}$ is contravariantly finite in 
$\Sigma \mathsf {Y}$. This is straightforward: let 
$d \in \Sigma \mathsf {Y}$ and take the truncation triangle with respect to 
$(\mathsf {X},\mathsf {Y})$,
\[ x \to d \to y \to \Sigma x. \]
Here, the morphism 
$x \to d$ is a right 
$\mathsf {X}$-approximation, so in particular, any morphism 
$h \to d$ with 
$h \in \mathsf {H}$ factors through 
$x \to d$. As 
$d \in \Sigma \mathsf {Y}$, it follows that 
$x \in \Sigma \mathsf {Y}$ because 
$\Sigma ^{-1}y \in \Sigma ^{-1}\mathsf {Y} \subset \Sigma \mathsf {Y}$. Hence, 
$x \in \mathsf {X} \cap \Sigma \mathsf {Y} = \mathsf {H}$, so, in particular, 
$x \to d$ is a right 
$\mathsf {H}$-approximation of 
$d$. Hence, 
$\mathsf {H}$ is contravariantly finite in 
$\Sigma \mathsf {Y}$ and therefore also in 
$\mathsf {D}$.
To see that 
$(\mathsf {X},\mathsf {Y})$ has enough Ext-injectives, let 
$(\mathsf {U},\mathsf {V})$ be the co-t-structure right adjacent to the t-structure 
$(\mathsf {X},\mathsf {Y})$, i.e. with 
$\mathsf {U} = \mathsf {Y}$, and note that 
$\mathsf {C} = \Sigma \mathsf {U} \cap \mathsf {V}$ is the coheart of this co-t-structure. We first claim that 
$\mathsf {C}$ is covariantly finite in 
$\Sigma \mathsf {Y} = \Sigma \mathsf {U}$. Let 
$y \in \mathsf {Y}$ and consider a 
$(\mathsf {U},\mathsf {V})$-approximation triangle of 
$\Sigma y$, 
$u \to \Sigma y \to c \to \Sigma u$. Extension closure of 
$\mathsf {U}$ and 
$\mathsf {V}$ shows that 
$c \in \Sigma \mathsf {U} \cap \mathsf {V} = \mathsf {C}$. Applying the functor 
$\mathsf {Hom}(-,\mathsf {C})$ to this triangle reveals that the morphism 
$\Sigma y \to c$ is a left 
$\mathsf {C}$-approximation. Hence, 
$\mathsf {C}$ is covariantly finite in 
$\Sigma \mathsf {Y}$.
Finally, we need to show that 
${}^\perp \mathsf {C} \cap \mathsf {H} = 0$. Suppose 
$0 \neq h \in {}^\perp \mathsf {C} \cap \mathsf {H}$ and again consider a 
$(\mathsf {U},\mathsf {V})$-approximation triangle as above: 
$u \to h \to c \to \Sigma u$. The argument above showed that 
$c \in \mathsf {C}$, whence the morphism 
$h \to c$ is zero, making 
$h$ a direct summand of 
$u \in \mathsf {U} = \mathsf {Y}$. Hence, 
$h \in \mathsf {X} \cap \mathsf {Y} = 0$, as required and 
$(\mathsf {X},\mathsf {Y})$ has enough Ext-injectives.
Remark 2.5 In the statement of Theorem 2.4, the full strength of the condition that the t-structure 
$(\mathsf {X},\mathsf {Y})$ is bounded is not strictly required. The statements involving enough (Ext-)injectives require the t-structure to be bounded above, i.e. 
$\mathsf {D} = \bigcup _{n\in \mathbb {Z}} \Sigma ^n \mathsf {Y}$; those involving enough (Ext-)projectives require the t-structure to be bounded below, i.e. 
$\mathsf {D} = \bigcup _{n \in \mathbb {Z}} \Sigma ^n \mathsf {X}$. These conditions are only used in the proof of the implication 
$(2) \Longrightarrow (3)$.
In the case that 
$\mathsf {D}$ is a saturated triangulated category, the statement of Theorem 2.4 becomes simpler and we can omit all mention of the existence of enough Ext-projectives or enough Ext-injectives and the projective and injective cohearts. We recall the definition of a saturated triangulated category from [Reference Bondal and KapranovBK90, Reference Bondal and van den BerghBvdB03].
Definition 2.6 Let 
$\mathsf {D}$ be a triangulated category and 
$F\colon \mathsf {D} \to \mathsf {mod}({\mathbf {k}})$ a cohomological functor.
(1) We say
$F$ is a functor of finite type if for any $d \in \mathsf {D}$, $F(\Sigma ^i d) \neq 0$ only for finitely many $i$.(2) If
$F$ is contravariant, then it is called representable if there is a functor isomorphism between $F$ and $\mathsf {Hom}_\mathsf {D} (-,x)$ for some $x \in \mathsf {D}$. The representing object $x$ is unique, up to isomorphism. Dually for covariant $F$.
The triangulated category 
$\mathsf {D}$ is said to be:
(3) of finite type if for every pair of objects
$x, y \in \mathsf {D}$, the space $\mathsf {Ext}^i_\mathsf {D} (x,y)$ is finite-dimensional and it vanishes for almost all $i$;(4) saturated if it is of finite type, and if every cohomological functor of finite type is representable.
Example 2.7 Examples of saturated triangulated categories include the bounded derived categories 
$\mathsf {D}^b(A)$ of finite-dimensional 
${\mathbf {k}}$-algebras 
$A$ of finite global dimension [Reference Bondal and KapranovBK90, Theorem 2.11], the bounded derived categories 
$\mathsf {D}^b(\mathsf {coh}(X))$ of coherent sheaves on a smooth projective variety 
$X$ [Reference Bondal and KapranovBK90, Theorem 2.14] (see also [Reference Bondal and van den BerghBvdB03, Theorem A.1] for a more general statement), and more generally, Ext-finite triangulated categories with a strong generator [Reference Bondal and van den BerghBvdB03, Theorem 1.3].
We now state the simplification of Theorem 2.4 for the saturated case.
Corollary 2.8 (Theorem C)
Let 
$\mathsf {D}$ be a Hom-finite, Krull–Schmidt, saturated triangulated category. Let 
$(\mathsf {X},\mathsf {Y})$ be a bounded t-structure in 
$\mathsf {D}$ with heart 
$\mathsf {H}$. The following are equivalent:
(1)
$\mathsf {H}$ is contravariantly finite (respectively, covariantly finite) in $\mathsf {D}$;(2)
$\mathsf {H}$ has enough injectives (respectively, projectives);(3)
$(\mathsf {X},\mathsf {Y})$ has a right (respectively, left) adjacent co-t-structure, i.e. there is a co-t-structure $(\mathsf {Y}, \mathsf {Y}^\perp )$ (respectively, $(\,^\perp \mathsf {X}, \mathsf {X})$).
Proof. Again, we show only the unbracketed statements; the bracketed statements are dual. The implications 
$(1) \Longrightarrow (2)$ and 
$(3) \Longrightarrow (1)$ are contained in the proof of Theorem 2.4. The implication 
$(2) \Longrightarrow (3)$ is due to [Reference BondarkoBon19, Theorem 5.3.1(IV)]; we include details for the convenience of the reader.
By the dual of [Reference Assem, Souto Salorio and TrepodeAST08, Lemma 1.3] (see also [Reference Nicolás, Saorín and ZvonarevaNSZ19, Lemma 2]), the functor 
$H^0(-)|_\mathsf {C} \colon \mathsf {C} \to \mathsf {inj}(\mathsf {H})$ is fully faithful, where 
$\mathsf {C} = \mathsf {Y}^\perp \cap \Sigma \mathsf {Y}$ is the injective coheart of 
$(\mathsf {X},\mathsf {Y})$. Moreover, by considering suitable truncation triangles, for each 
$c \in \mathsf {C}$ there is a natural isomorphism 
$\mathsf {Hom}_\mathsf {D}(-,c) \simeq \mathsf {Hom}_\mathsf {H}(H^0(-),H^0(c))$. We claim that 
$H^0(-)|_\mathsf {C}$ is an equivalence of categories, that is, for each 
$e \in \mathsf {inj}(\mathsf {H})$, we need to show that there is an isomorphism 
$H^0(c) \simeq e$ for some 
$c \in \mathsf {C}$.
Consider the functor 
$\mathsf {Hom}_\mathsf {H}(H^0(-),e) \colon \mathsf {D} \to \mathsf{mod}({{\mathbf {k}}})$. By saturatedness, 
$\mathsf {Hom}_\mathsf {H}(H^0(-),e)$ is a cohomological functor of finite type, and hence is representable, i.e. there exists an object 
$c \in \mathsf {D}$ such that 
$\mathsf {Hom}_\mathsf {H}(H^0(-),e) \simeq \mathsf {Hom}_\mathsf {D}(-,c)$. We note that 
$c \in \mathsf {C}$ because 
$H^0(\Sigma x) = 0$ for 
$x \in \mathsf {X}$ and 
$H^0(y) = 0$ for 
$y \in \mathsf {Y}$, which together imply that 
$\mathsf {Hom}_\mathsf {D}(\Sigma \mathsf {X},c) = 0$, putting 
$c \in (\Sigma \mathsf {X})^\perp = \Sigma \mathsf {Y}$, and 
$\mathsf {Hom}_\mathsf {D}(\mathsf {Y},c) = 0$, putting 
$c \in \mathsf {Y}^\perp$.
Combining the natural isomorphisms in the two preceding paragraphs and restricting to 
$\mathsf {H}$ gives rise to a natural isomorphism
\[ \theta \colon \mathsf{Hom}_\mathsf{H}(-, H^0(c)) \to \mathsf{Hom}_\mathsf{H}(-,e). \]
Let 
$\alpha = \theta _{H^0(c)}(1_{H^0(c)})$ and 
$\beta = \theta _e^{-1}(1_e)$. Applying the natural isomorphism to the morphism 
$\alpha \colon H^0(c) \to e$ gives the following commutative diagram.
Chasing 
$\beta \colon e \to H^0(c)$ through this diagram shows that 
$\beta \alpha = 1_{H^0(c)}$. Similarly, chasing 
$\alpha$ through the corresponding diagram constructed using 
$\beta$ shows 
$\alpha \beta = 1_e$. Hence, 
$e \simeq H^0(c)$ and 
$H^0(-)|_\mathsf {C} \colon \mathsf {C} \to \mathsf {inj}(\mathsf {H})$ is an equivalence of categories. Note, in particular, that 
$\beta \colon e \to H^0(c)$ provides the required 
$\mathsf {H}$-monomorphism so that we can now apply the argument 
$(2) \implies (3)$ in the proof of Theorem 2.4.
Remark 2.9 The argument in the proof of Corollary 2.8 also shows that the condition that the t-structure 
$(\mathsf {X},\mathsf {Y})$ has enough Ext-injectives (respectively, Ext-projectives) is implicit in the saturated case because condition 
$(3)$ remains unchanged in both statements.
Using Corollary 2.8 we are able to establish the existence of Auslander–Reiten sequences in hearts of bounded t-structures inside saturated triangulated categories.
Corollary 2.10 Suppose 
$\mathsf {D}$ is a Hom-finite, Krull–Schmidt, saturated triangulated category. Let 
$\mathsf {H}$ be the heart of a bounded t-structure in 
$\mathsf {D}$.
(1) If
$\mathsf {H}$ has enough injectives, then any indecomposable object of $\mathsf {H}$ which is not Ext-projective is the third object of an Auslander–Reiten sequence.(2) If
$\mathsf {H}$ has enough projectives, then any indecomposable object of $\mathsf {H}$ which is not Ext-injective is the first object of an Auslander–Reiten sequence.
Proof. We only prove the first statement; the second is dual. Suppose 
$h \in \mathsf {ind}(\mathsf {H})$ is not Ext-projective, i.e. 
$\mathsf {Ext}^1_{\mathsf {H}}(h,-) = \mathsf {Hom}_{\mathsf {D}}(h,\Sigma -)|_\mathsf {H} \neq 0$. As 
$\mathsf {D}$ is saturated, it has a Serre functor; see, e.g., [Reference KawamataKaw09]. Therefore, by [Reference Reiten and van den BerghRvdB02, Theorem I.2.4], 
$\mathsf {D}$ has Auslander–Reiten triangles. In particular, there is an Auslander–Reiten triangle 
$x \to y \to h \to \Sigma x$ in 
$\mathsf {D}$. As 
$\mathsf {H}$ has enough injectives, by Corollary 2.8, 
$\mathsf {H}$ is contravariantly finite in 
$\mathsf {D}$. Hence, 
$x$ admits a minimal right 
$\mathsf {H}$-approximation. Thus, we can now apply [Reference JørgensenJør09, Theorem 3.1] to conclude that there is an Auslander–Reiten sequence 
$0 \to h' \to h'' \to h \to 0$ in 
$\mathsf {H}$.
Finally, we remark that Theorem 2.4 allows us to recognise module categories of finite-dimensional algebras via the approximation theory of the heart inside an ambient triangulated category.
Corollary 2.11 Let 
$\mathsf{D}$ be a Hom-finite saturated 
$\mathbf{k}$-linear triangulated category. Suppose 
$(\mathsf{X},\mathsf{Y})$ is an algebraic t-structure in 
$\mathsf{D}$ with heart 
$\mathsf{H}$. The heart 
$\mathsf{H}$ is covariantly finite in 
$\mathsf{D}$ if and only if 
$\mathsf{H} \simeq \mathsf{mod}(A)$ for a finite-dimensional 
$\mathbf{k}$-algebra A.
Proof. By [Reference BassBas68, p. 55], since 
$\mathsf {H}$ is length with finitely many simple objects, 
$\mathsf {H}$ has a projective generator if and only if 
$\mathsf {H} \simeq \mathsf{mod}(A)$ for some finite-dimensional 
${\mathbf {k}}$-algebra A. The result now follows from Corollary 2.8 using the direct sum of the projective covers of each of the finitely many simple objects to obtain a projective generator.
Corollary 2.12 Let 
$A$ be a finite-dimensional 
${\mathbf {k}}$-algebra. If 
$(\mathsf {X},\mathsf {Y})$ is an algebraic t-structure in 
$\mathsf {D}^b(A)$ with heart 
$\mathsf {H}$, then 
$\mathsf {H}$ is functorially finite in 
$\mathsf {D}^b(A)$.
Proof. Let 
$A$ be a finite-dimensional algebra and suppose 
$(\mathsf {X},\mathsf {Y})$ is an algebraic t-structure in 
$\mathsf {D}^b(A)$. We show that 
$\mathsf {H}$ is covariantly finite in 
$\mathsf {D}$; dually one can show 
$\mathsf {H}$ is contravariantly finite. By the König–Yang correspondences [Reference Koenig and YangKY14] and [Reference Aihara and IyamaAI12, Proposition 2.20], the projective coheart 
$\mathsf {S} = {}^\perp \Sigma \mathsf {X} \cap \mathsf {X}$ is a silting subcategory of 
$\mathsf {K}^b(\mathsf {proj}(A))$ such that 
$\mathsf {S} = \mathsf {add}(s)$ for some object 
$s \in \mathsf {K}^b(\mathsf {proj}(A))$. In particular, 
$\mathsf {S}$ is a functorially finite subcategory of 
$\mathsf {D}^b(A)$. Furthermore, 
$(\mathsf {X},\mathsf {Y}) = ((\Sigma ^{<0} \mathsf {S})^\perp, (\Sigma ^{\geqslant 0} \mathsf {S})^\perp )$ by [Reference Koenig and YangKY14, Theorem 6.1]. Now, applying [Reference Iyama and YangIY18, Proposition 3.2], we observe that 
$(\mathsf {cosusp}\ {\Sigma ^{-1} \mathsf {S}}, (\Sigma ^{<0} \mathsf {S})^\perp )$ is a co-t-structure in 
$\mathsf {D}^b(A)$ which is left adjacent to the t-structure 
$(\mathsf {X},\mathsf {Y})$. Hence, by Theorem 2.4, 
$\mathsf {H}$ is covariantly finite in 
$\mathsf {D}^b(A)$.
The following example, however, shows that there can be algebraic hearts inside a Hom-finite Krull–Schmidt triangulated category which are not necessarily functorially finite.
Example 2.13 Let 
$\mathsf {H}$ be a standard stable homogeneous tube. This is a length category in which every object is uniserial. Moreover, 
$\mathsf {H}$ contains a single simple object, but no injective or projective objects except the zero object. It has infinitely many indecomposable objects. The category 
$\mathsf {D} = \mathsf {D}^b(\mathsf {H})$ is a 
$1$-Calabi–Yau triangulated category in which the only torsion pairs are trivial or shifts of the standard t-structure, which is bounded, see [Reference Coelho Simões and PauksztelloCP16, Theorem 9.1]. As 
$\mathsf {H}$ is length with one isoclass of simple objects, it is algebraic; but it does not have enough projectives or injectives and is therefore neither contravariantly finite nor covariantly finite in 
$\mathsf {D}$.
The next example gives a typical application of the theorem where the intrinsic property (presence or absence of enough injective and projective objects) is used to make a statement about finiteness.
Example 2.14 Let 
$\mathsf {H} = \mathsf{mod}({{\mathbf {k}}\tilde {A}_{1}})$ be the category of finite-dimensional representations of the Kronecker quiver. In the derived category 
$\mathsf {D} = \mathsf {D}^b(\mathsf {H})$, this heart is obviously algebraic. As is well known, 
$\mathsf {D}$ is equivalent to the bounded derived category of coherent sheaves on the projective line 
$\mathbb {P}^1$ over 
${\mathbf {k}}$, giving rise to another heart 
$\mathsf {H}' = \mathsf {coh}(\mathbb {P}^1)$ in 
$\mathsf {D}$. The abelian category 
$\mathsf {H}'$ has neither injective nor projective objects apart from 0. Hence, by Theorem 2.4, the heart 
$\mathsf {H}'$ is neither covariantly nor contravariantly finite in 
$\mathsf {D}$.
Remark 2.15 It would be interesting to investigate when Corollary 2.8 holds without the saturatedness assumption on the triangulated category.
As an example, consider 
$\mathsf {D} = \mathsf {D}^b(\mathsf {Qcoh}(\mathbb {P}^1))$, the bounded derived category of quasi-coherent sheaves on 
$\mathbb {P}^1$. The standard heart 
$\mathsf {H} = \mathsf {Qcoh}(\mathbb {P}^1)$ is a hereditary abelian category with enough injective objects but no nonzero projective objects. The hereditary property, together with the fact that 
$\mathsf {H}$ is the heart of a split t-structure in 
$\mathsf {D}$, means the injective coheart 
$\mathsf {C} = \mathsf {Y}^\perp \cap \Sigma \mathsf {Y} = (\Sigma ^{-1} \mathsf {H})^\perp \cap \mathsf {H} = \mathsf {inj}(\mathsf {H})$. Hence, condition 
$(2)$ in Theorem 2.4 simplifies to the condition that 
$\mathsf {H}$ has enough injectives. By Theorem 2.4, we can conclude that 
$\mathsf {H}$ is contravariantly finite in 
$\mathsf {D}$. We can also see this explicitly: every object in 
$\mathsf {D}$ splits into a finite direct sum of its cohomology sheaves. Let 
$d$ be an object of 
$\mathsf {D}$ which we can assume to be 
$d = \Sigma ^i A$ with 
$A \in \mathsf {H}$ and 
$i \in \mathbb {Z}$. Nonzero right 
$\mathsf {H}$-approximations 
$H \to \Sigma ^i A$ can only exist if 
$i=0$ or 
$i=1$. If 
$i=0$, they are trivial (take 
$H=A$). If 
$i=1$, let 
$I$ be an injective hull of 
$A$, leading to a short exact sequence 
$0 \to A \to I \to H \to 0$, i.e. 
$H$ is the first co-syzygy of 
$A$. The resulting morphism 
$H \to \Sigma A$ is a right 
$\mathsf {H}$-approximation.
We observe that the lack of projective objects means that 
$\mathsf {H}$ is not an enveloping subcategory of 
$\mathsf {D}$. As previously, the hereditary property means that it is sufficient to consider nontrivial minimal left 
$\mathsf {H}$-approximations only for objects of 
$\Sigma ^{-1} \mathsf {H}$. Let 
$A \in \mathsf {H}$, take a minimal left 
$\mathsf {H}$-approximation of 
$\Sigma ^{-1} A$ and extend it to a distinguished triangle 
${\Sigma ^{-1} H \to \Sigma ^{-1} P \to \Sigma ^{-1} A \to H}$. As 
$A, H \in \mathsf {H}$, we have 
$P \in \mathsf {H}$. Because the approximation is minimal, the Wakamatsu lemma tells us that 
$\Sigma ^{-1} P \in {}^\perp \mathsf {H}$. This means that 
$P \in \mathsf {H} \cap {}^\perp (\Sigma \mathsf {H}) = \mathsf {proj}(\mathsf {H}) = 0$. Therefore, no such nontrivial minimal left 
$\mathsf {H}$-approximation exists and, hence, 
$\mathsf {H}$ is not an enveloping subcategory of 
$\mathsf {D}$.
We also expect that 
$\mathsf {H}$ is not covariantly finite in 
$\mathsf {D}$. The above argument fails to apply because 
$\mathsf {D}$ is not saturated. This expectation is consistent with Theorem 2.4: the projective coheart of the standard t-structure is 
$\mathsf {S} = {}^\perp (\Sigma \mathsf {X}) \cap \mathsf {X} = {}^\perp (\Sigma \mathsf {H}) \cap \mathsf {H} = \mathsf {proj}(\mathsf {H}) = 0$ and, hence, the standard heart 
$\mathsf {H} = \mathsf {Qcoh}(\mathbb {P}^1)$ also does not have enough Ext-projectives.
3. Orthogonal collections
In this section, we recall the various notions of orthogonal collections and then establish some useful characterisations of them. The main references for the definitions in this section are [Reference Coelho SimõesCoe12, Reference Coelho SimõesCoe15, Reference Coelho SimõesCoe17, Reference Coelho Simões and PauksztelloCP20, Reference DugasDug15, Reference Koenig and LiuKL12]. From now on, we assume that the field 
${\mathbf {k}}$ is algebraically closed.
Definitions 3.1 A collection of objects 
$\mathsf {S}$ in 
$\mathsf {D}$ is called a 
$1$-orthogonal collection (or simply orthogonal collection) if 
$\dim \mathsf {Hom}_\mathsf {D}(x,y) = \delta _{xy}$ for every 
$x,y \in \mathsf {S}$. Let 
$w \geqslant 1$ be an integer. An orthogonal collection 
$\mathsf {S}$ is said to be
(i) (if
$w > 1$) $w$-orthogonal if $\mathsf {Hom}_\mathsf {D}(\Sigma ^k x,y) = 0$ for $1 \leqslant k \leqslant w-1$ and $x,y \in \mathsf {S}$;(ii)
$\infty$-orthogonal if $\mathsf {Hom}_\mathsf {D}(\Sigma ^k x,y) = 0$ for $k \geqslant 1$ and $x,y \in \mathsf {S}$;(iii) a
$w$-simple-minded system if it is $w$-orthogonal and $\mathsf {D} = \langle \mathsf {S} \rangle * \Sigma ^{-1} \langle \mathsf {S} \rangle * \cdots * \Sigma ^{1-w} \langle \mathsf {S} \rangle$;(iv) a simple-minded collection if it is
$\infty$-orthogonal and $\mathsf {D} = \mathsf {thick}_{\mathsf {D}}(\mathsf {S})$;(v) a left
$w$-Riedtmann configuration if it is $w$-orthogonal and $\bigcap _{k=0}^{w-1} (\Sigma ^k \mathsf {S})^\perp = 0$;(vi) a right
$w$-Riedtmann configuration if it is $w$-orthogonal and $\bigcap _{k=0}^{w-1} {}^\perp (\Sigma ^{-k} \mathsf {S}) = 0$;(vii) a
$w$-Riedtmann configuration if it is both a left $w$-Riedtmann configuration and a right $w$-Riedtmann configuration; and(viii) an
$\infty$-Riedtmann configuration if it is $\infty$-orthogonal and ${}^\perp (\Sigma ^{< 0} \mathsf {S}) \cap (\Sigma ^{\geqslant 0} \mathsf {S})^\perp = 0$.
Our methods work in the case that 
${\mathbf {k}}$ is not algebraically closed provided one modifies the definition of orthogonal collection to require that 
$\mathsf {Hom}_\mathsf {D}(x,x)$ is a division ring for each 
$x$ in the orthogonal collection. For simplicity of exposition, we choose to work over algebraically closed fields, so that when considering 
$\mathsf {D}^b({\mathbf {k}} Q)$ one can work with quiver representations instead of the more technical representations of species.
An orthogonal collection is called a system of orthogonal bricks in [Reference PogorzalyPog94], a set of (pairwise) orthogonal bricks in [Reference DugasDug15], and a semibrick in [Reference AsaiAsa20]. In [Reference Iyama and JinIJ20, Reference JinJin20, Reference JinJin19] 
$w$-Riedtmann configurations are called 
$(-w)$-Calabi–Yau configurations in light of [Reference JinJin20, Theorem 6.2] which asserts that if 
$\mathsf {S}$ is a 
$w$-Riedtmann configuration, then 
$\mathbb {S} \Sigma ^w \mathsf {S} = \mathsf {S}$.
Remark 3.2 We have chosen to call collections with vanishing morphisms between distinct objects ‘
$1$-orthogonal collections’ rather than ‘
$0$-orthogonal collections’ because in 
$(-1)$-Calabi–Yau categories 
$\mathsf {Hom}(x,y) \simeq D\,\mathsf {Hom}(\Sigma y, x)$, which means that 
$1$-orthogonal collections with vanishing morphisms are the appropriate notion for 
$(-1)$-CY categories. As such, one should think of a 
$w$-orthogonal collection (respectively, 
$w$-simple-minded systems, resp. 
$w$-Riedtmann configuration) as being adapted for 
$(-w)$-CY categories.
Let 
$\mathsf {X} \subseteq \mathsf {D}$ be a collection of objects in 
$\mathsf {D}$. We set 
$(\mathsf {X})_1 = \mathsf {X}$ and 
$(\mathsf {X})_n = \mathsf {X} * (\mathsf {X})_{n-1}$. We now recall some basic properties of orthogonal collections.
Lemma 3.3 Let 
$\mathsf {S}$ be an orthogonal collection in 
$\mathsf {D}$. Then the following assertions hold:
(1) ([Reference DugasDug15, Lemma 2.7])
$(\mathsf {S})_n$ is closed under direct summands for each $n \geqslant 1$;(2) ([Reference DugasDug15, Lemma 2.3])
$\langle \mathsf {S} \rangle = \bigcup _{n \geqslant 1} (\mathsf {S})_n$;(3) ([Reference Coelho Simões and PauksztelloCP20, Theorem 2.11] & [Reference DugasDug15, Theorem 3.3]) if
$\mathsf {S} \subseteq \mathsf {T}$ for an orthogonal collection $\mathsf {T}$ in $\mathsf {D}$, then $\langle \mathsf {S} \rangle$ is functorially finite in $\langle \mathsf {T} \rangle$.
Lemma 3.3
$(2)$ means that the following definition makes sense.
Definition 3.4 [Reference DugasDug15, Definition 2.5]
Let 
$\mathsf {S}$ be an orthogonal collection in 
$\mathsf {D}$. The 
$\mathsf {S}$-length (or simply length) of 
$x \in \langle \mathsf {S} \rangle$ is the smallest natural number 
$n$ such that 
$x \in (\mathsf {S})_n$.
Recall the following characterisation of 
$w$-simple-minded systems from [Reference Coelho Simões and PauksztelloCP20].
Proposition 3.5 [Reference Coelho Simões and PauksztelloCP20, Proposition 2.13]
Let 
$\mathsf {S}$ be a collection of indecomposable objects in 
$\mathsf {D}$ and let 
$w \geqslant 1$ be an integer. The following conditions are equivalent:
(1)
$\mathsf {S}$ is a $w$-simple-minded system;(2)
$\mathsf {S}$ is a right $w$-Riedtmann configuration such that $\langle \mathsf {S} \rangle$ is covariantly finite in $\mathsf {D}$;(3)
$\mathsf {S}$ is a left $w$-Riedtmann configuration such that $\langle \mathsf {S} \rangle$ is contravariantly finite in $\mathsf {D}$;(4)
$\mathsf {S}$ is a $w$-Riedtmann configuration such that $\langle \mathsf {S} \rangle$ is functorially finite in $\mathsf {D}$.
We next provide an analogue of Proposition 3.5 for simple-minded collections.
Proposition 3.6 Let 
$\mathsf {S}$ be a collection of indecomposable objects in 
$\mathsf {D}$. Then 
$\mathsf {S}$ is a simple-minded collection if and only if 
$\mathsf {S}$ is an 
$\infty$-Riedtmann configuration such that 
$\mathsf {susp}\ \mathsf {S}$ is contravariantly finite in 
$\mathsf {D}$ and 
$\mathsf {cosusp}\ \mathsf {S}$ is covariantly finite in 
$\mathsf {D}$.
Proof. Suppose that 
$\mathsf {S}$ is a simple-minded collection in 
$\mathsf {D}$. As both simple-minded collections and 
$\infty$-Riedtmann configurations are 
$\infty$-orthogonal collections, we only need to check the other defining properties of 
$\infty$-Riedtmann configurations. Then, by definition, 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {S}) = \mathsf {D}$ and by, for example, [Reference Coelho Simões and PauksztelloCP20, Lemma 2.7] we have
\[ \mathsf{D} = \bigcup_{n > m} \Sigma^n \langle \mathsf{S} \rangle * \Sigma^{n-1} \langle \mathsf{S} \rangle * \cdots * \Sigma^{m+1} \langle \mathsf{S} \rangle * \Sigma^m \langle \mathsf{S} \rangle. \]
It therefore follows immediately that 
$(\mathsf {susp}\ \mathsf {S},\mathsf {cosusp}\ \Sigma ^{-1} \mathsf {S})$ is a bounded t-structure in 
$\mathsf {D}$, and, in particular, 
$\mathsf {susp}\ \mathsf {S}$ is contravariantly finite and 
$\mathsf {cosusp}\ \mathsf {S}$ is covariantly finite. Finally, 
$(\Sigma ^{\geqslant 0} \mathsf {S})^\perp = (\mathsf {susp}\ \mathsf {S})^\perp = \mathsf {cosusp}\ \Sigma ^{-1} \mathsf {S}$ and 
${}^\perp (\Sigma ^{< 0} \mathsf {S}) = {}^\perp (\mathsf {cosusp}\ \Sigma ^{-1} \mathsf {S}) = \mathsf {susp}\ \mathsf {S}$, so that 
${}^\perp (\Sigma ^{< 0} \mathsf {S}) \cap (\Sigma ^{\geqslant 0} \mathsf {S})^\perp = \mathsf {susp}\ \mathsf {S} \cap \mathsf {cosusp}\ \Sigma ^{-1} \mathsf {S} = 0$.
Conversely, suppose that 
$\mathsf {S}$ is an 
$\infty$-Riedtmann configuration such that 
$\mathsf {susp}\ \mathsf {S}$ is contravariantly finite in 
$\mathsf {D}$ and 
$\mathsf {cosusp}\ \mathsf {S}$ is covariantly finite in 
$\mathsf {D}$. To see that 
$\mathsf {S}$ is a simple-minded collection we need only to check that 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {S}) = \mathsf {D}$. Let 
$d$ be an object of 
$\mathsf {D}$. As 
$\mathsf {susp}\ \mathsf {S}$ is contravariantly finite in 
$\mathsf {D}$ there is a decomposition triangle 
$x\rightarrow d\rightarrow y\rightarrow \Sigma x$ with respect to the t-structure 
$(\mathsf {susp}\ \mathsf {S}, (\Sigma ^{\geqslant 0} \mathsf {S})^\perp )$. Now, because 
$\mathsf {cosusp}\ \mathsf {S}$ is covariantly finite in 
$\mathsf {D}$ there is a decomposition triangle of 
$y$, 
$\Sigma ^{-1} v \to u \to y \to v$ with respect to the t-structure 
$({}^\perp (\Sigma ^{<0} \mathsf {S}), \mathsf {cosusp}\ \Sigma ^{-1} \mathsf {S})$. Note that 
$\mathsf {cosusp}\ \Sigma ^{-1} \mathsf {S} \subseteq (\Sigma ^{\geqslant 0} \mathsf {S})^\perp$ so that 
$\Sigma ^{-1} v \in (\Sigma ^{\geqslant -1} \mathsf {S})^\perp \subseteq (\Sigma ^{\geqslant 0} \mathsf {S})^\perp$. As 
$(\Sigma ^{\geqslant 0} \mathsf {S})^\perp$ is a perpendicular category, it is closed under extensions. It follows that 
$u \in {}^\perp (\Sigma ^{<0} \mathsf {S}) \cap (\Sigma ^{\geqslant 0} \mathsf {S})^\perp$. Hence, because 
$\mathsf {S}$ is 
$\infty$-Riedtmann, we obtain that 
$u = 0$ and 
$y \simeq v$. In particular, we obtain
\[ d \in \mathsf{susp}\ \mathsf{S} * \mathsf{cosusp}\ \Sigma^{{-}1} \mathsf{S} = \mathsf{thick}_{\mathsf{D}}(\mathsf{S}). \]
Hence, 
$\mathsf {D} = \mathsf {thick}_{\mathsf {D}}(\mathsf {S})$ and 
$\mathsf {S}$ is a simple-minded collection.
Finally, we end this section with the following restatement of Corollary 2.12 in the language of simple-minded collections.
Corollary 3.7 Suppose 
$\mathsf {D} = \mathsf {D}^b(A)$ for some finite-dimensional 
${\mathbf {k}}$-algebra 
$A$. If 
$\mathsf {S}$ is a simple-minded collection in 
$\mathsf {D}$, then 
$\langle \mathsf {S} \rangle$ is functorially finite in 
$\mathsf {D}$.
4. Simple-minded collections versus $w$-simple minded systems
Let 
$Q$ be a finite acyclic quiver and 
$w \geqslant 1$. Recall from § 1.2 the construction of the negative cluster category 
$\mathsf {C}_{-w} = \mathsf {C}_{-w}({\mathbf {k}} Q)$ as an orbit category of 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$ and the fundamental domain 
$\mathcal {F}_{-w} \mathrel {\mathop :}= \mathsf {X} \cap \Sigma ^w \mathbb {S} \mathsf {Y}$. The aim of this section is to establish the following theorem, which generalises the case of 
$Q$ simply-laced Dynkin of [Reference Iyama and JinIJ20, Theorem 1.2]. The proof of Iyama and Jin uses that subcategories of Hom-finite triangulated categories with finitely many indecomposable objects are automatically functorially finite; we use Theorem 2.4 to obtain functorial finiteness in our setting.
Theorem 4.1 (Theorem A)
Let 
$Q$ be an acyclic quiver. The natural projection functor 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}$ induces a bijection
\[ \pi \colon \Big\{ \begin{matrix} \textrm{simple-minded collections of}\\ \mathsf{D}^b({\mathbf{k}}\,Q)\ \textrm{contained in}\ \mathcal{F}_{{-}w}\end{matrix}\Big\} \stackrel{1-1}{\longleftrightarrow} \Big\{\begin{matrix} w\textrm{-simple-minded systems}\\ \textrm{in}\ \mathsf{C}_{{-}w}\end{matrix}\Big\}. \] The proof of this theorem comes in two parts. We must first establish that the map of the theorem induced by the functor 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}$, which, by abuse of notation, we also call 
$\pi$, is well defined and secondly that the map is surjective. Once we know that the map 
$\pi$ is well defined, injectivity follows immediately because the projection functor 
$\pi$ induces a bijection between 
$\mathsf {ind}(\mathsf {C}_{-w})$ and 
$\mathsf {ind}(\mathcal {F}_{-w})$, where 
$\mathcal {F}_{-w}$ is the fundamental domain; see § 1.2 for notation.
4.1 The induced map $\pi$ is well defined
In this section, we establish the following.
Proposition 4.2 Let 
$Q$ be an acyclic quiver. The natural functor 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}$ induces a well-defined map
\[ \pi \colon \Big\{\begin{matrix} \textrm{simple-minded collections of}\\ \mathsf{D}^b({\mathbf{k}}\,Q)\ \textrm{contained in}\ \mathcal{F}_{{-}w}\end{matrix}\Big\} \longrightarrow \Big\{\begin{matrix} w\textrm{-simple-minded systems}\\ \textrm{in}\ \mathsf{C}_{{-}w}\end{matrix}\Big\}. \] In [Reference Iyama and JinIJ20, Proposition 3.6], Iyama and Jin show that 
$\pi$ induces a well-defined map
\[ \tilde{\pi} \colon \Big\{\begin{matrix} \textrm{simple-minded collections of}\\ \mathsf{D}^b({\mathbf{k}}\,Q)\ \textrm{contained in}\ \mathcal{F}_{{-}w}\end{matrix}\Big\} \longrightarrow \{\textit{w}\textrm{-Riedtmann configurations in}\ \mathsf{C}_{{-}w}\}. \]
When 
$Q$ is simply laced Dynkin, by Proposition 3.5, this is enough to establish Proposition 4.2. However, more work is required for an arbitrary acyclic quiver 
$Q$. In fact, the following example illustrates that 
$\tilde {\pi }$ is not surjective when 
$Q$ is not simply laced Dynkin.
Example 4.3 Let 
$Q = \tilde {A}_{1}$ be the Kronecker quiver and 
$w = 1$. Partition the set of homogeneous tubes into two nonempty, disjoint sets 
$\Lambda$ and 
$\Omega$ and set
\[ \mathsf{S} \mathrel{\mathop:}= \{ S_\lambda \mid \lambda \in \Lambda\} \cup \{ \Sigma S_\omega \mid \omega \in \Omega\}, \]
where 
$S_\lambda$ (respectively, 
$S_\omega$) denotes the quasi-simple modules lying on the mouth of the tubes indexed by 
$\Lambda$ (respectively, 
$\Omega$). Then 
$\mathsf {S}$ is a 
$1$-Riedtmann configuration in 
$\mathsf {C}_{-1} \mathrel {\mathop :}= \mathsf {C}_{-1} ({\mathbf {k}} \tilde {A}_{1})$; the required Hom-vanishing needs 
$\Lambda \neq \varnothing$ and 
$\Omega \neq \varnothing$. However, 
$\mathsf {S}$ is not a simple-minded collection in 
$\mathsf {D} \mathrel {\mathop :}= \mathsf {D}^b({\mathbf {k}} \tilde {A}_{1})$ because 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {S}) \neq \mathsf {D}$. Note also that 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-1}}$ is not functorially finite in 
$\mathsf {C}_{-1}$ and so 
$\mathsf {S}$ is not a simple-minded system in 
$\mathsf {C}_{-1}$.
To prove Proposition 4.2, we need some lemmas. Recall 
$F = \Sigma ^w \mathbb {S}\colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {D}^b({\mathbf {k}} Q)$.
Lemma 4.4 Let 
$\mathsf {S}$ be an 
$\infty$-orthogonal collection of 
$\mathsf {D}^b({\mathbf {k}} Q)$ contained in 
$\mathcal {F}_{-w}$.
(1) The set
$\{F^n \mathsf {S} \mid n \in \mathbb {Z}\}$ is an orthogonal collection in $\mathsf {D}^b({\mathbf {k}} Q)$.(2) For
$k \geqslant 1$, we have $\mathsf {Ext}^1_{\mathsf {D}^b({\mathbf {k}} Q)} (\mathsf {S}, F^k \mathsf {S}) = 0$.
Proof. To prove statement (1), it is enough to show that 
$\mathsf {Hom}_{\mathsf {D}} (S_1, F^n S_2) = 0$ for 
$S_1, S_2 \in \mathsf {S}$ and 
$n \in \mathbb {Z} \setminus \{0\}$ because 
$\mathsf {S}$ is an orthogonal collection in 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$ and 
$F$ is an autoequivalence. For 
$n = 1$, we have 
$\mathsf {Hom}_{\mathsf {D}} (S_1, F S_2) \simeq D\, \mathsf {Hom}_{\mathsf {D}} (\Sigma ^w S_2, S_1) = 0$, since 
$w \geqslant 1$ and 
$\mathsf {S}$ is an 
$\infty$-orthogonal collection.
Now consider 
$n=2$. Recall that 
$(\mathsf {X},\mathsf {Y})$ denotes the standard t-structure on 
$\mathsf {D}$. As 
$S_1 \in \mathcal {F}_{-w} \subseteq \Sigma ^{w} \mathbb {S} \mathsf {Y}$, there exists 
$Y \in \mathsf {Y}$ such that 
$S_1 = \Sigma ^{w} \mathbb {S} Y = FY$. Hence, 
$\mathsf {Hom}_{\mathsf {D}} (S_1, F^2 S_2) \simeq D\, \mathsf {Hom}_{\mathsf {D}} (\Sigma ^{w} S_2, Y) = 0$, because 
$S_2$, and so 
$\Sigma ^{w} S_2$, lie in 
$\mathsf {X}$.
Now let 
$n > 2$. By the hereditary property, we have 
$F^n S_2 \in \mathbb {S}^n \Sigma ^{nw} \mathsf {X} \subseteq \Sigma ^{nw} \mathsf {X}$ and 
$S_1 \in \mathbb {S} \Sigma ^{w} \mathsf {Y} \subseteq \Sigma ^{w+1} \mathsf {Y}$. Therefore, 
$\mathsf {Hom}_{\mathsf {D}} (S_1, F^n S_2) \simeq \mathsf {Hom}_{\mathsf {D}} (Y,\Sigma ^{(n-1)w-1} X)$, for some 
$Y \in \mathsf {Y}$ and 
$X \in \mathsf {X}$. As 
$(n-1) w -1 \geqslant 1$, it follows that 
$\mathsf {Hom}_{\mathsf {D}} (S_1, F^n S_2) = 0$, again by the hereditary property.
Finally, let 
$n \leqslant -1$. As 
$S_2 \in \Sigma ^{w} \mathbb {S} \mathsf {Y}$, we get 
$F^n S_2 \in \Sigma ^{(n+1)w} \mathbb {S}^{n+1} \mathsf {Y} \subseteq \Sigma ^{(n+1)w} \mathsf {Y} \subseteq \mathsf {Y}$ by the hereditary property, the fact that 
$\mathsf {Y}$ is the co-aisle of a t-structure, and 
$(n+1)w \leqslant 0$. It follows that 
$\mathsf {Hom}_{\mathsf {D}} (S_1, F^n S_2) = 0$ because 
$S_1 \in \mathsf {X}$.
Statement 
$(2)$ follows from the 
$\infty$-orthogonality property of 
$\mathsf {S}$ when 
$k = 1$, and from the argument above for 
$n >2$, when 
$k \geqslant 2$.
Corollary 4.5 Let 
$\mathsf {S}$ be an 
$\infty$-orthogonal collection of 
$\mathsf {D}^b({\mathbf {k}} Q)$ contained in 
$\mathcal {F}_w$. Then 
$\langle F^n \mathsf {S} \rangle _{\mathsf {D}^b({\mathbf {k}} Q)} * \langle \mathsf {S} \rangle _{\mathsf {D}^b({\mathbf {k}} Q)} \subseteq \langle \mathsf {S} \rangle _{\mathsf {D}^b({\mathbf {k}} Q)} * \langle F^n \mathsf {S} \rangle _{\mathsf {D}^b({\mathbf {k}} Q)}$, for all 
$n \geqslant 1$.
Proof. Given 
$D \in \langle F^n \mathsf {S} \rangle _{\mathsf {D}} * \langle \mathsf {S} \rangle _{\mathsf {D}}$, we have a triangle 
$F^n S_1\stackrel {}{\longrightarrow } D\stackrel {}{\longrightarrow } S_2\stackrel {\alpha }{\longrightarrow } \Sigma F^n S_1$, with 
$S_1, S_2 \in \langle \mathsf {S} \rangle$. It follows from Lemma 4.4(2) that 
$\alpha = 0$. Hence, the triangle splits, and 
$D \simeq S_2 \oplus F^n S_1 \in \langle \mathsf {S} \rangle _{\mathsf {D}} * \langle F^n \mathsf {S} \rangle _{\mathsf {D}}$.
Following Lemma 4.4 and Corollary 4.5, for an 
$\infty$-orthogonal collection 
$\mathsf {S}$ of 
$\mathsf {D}^b({\mathbf {k}} Q)$ contained in 
$\mathcal {F}_{-w}$, we define the following extension-closed subcategory of 
$\mathsf {D}^b({\mathbf {k}} Q)$:
\[ \mathcal{E}_\mathsf{S} \mathrel{\mathop:}= \langle F^n \mathsf{S} \mid n \in \mathbb{Z} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)}. \]
We now show that each object of 
$\mathcal {E}_\mathsf {S}$ admits a filtration by objects in 
$\{ F^n \mathsf {S} \mid n \in \mathbb {Z}\}$.
Lemma 4.6 Let 
$\mathsf {S}$ be an 
$\infty$-orthogonal collection of 
$\mathsf {D}^b({\mathbf {k}} Q)$ contained in 
$\mathcal {F}_{-w}$. Then 
$\mathcal {E}_\mathsf {S}$ is closed under direct summands and
\[ \mathcal{E}_\mathsf{S} = \bigcup_{m< n} \langle F^m \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} * \langle F^{m+1} \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} * \cdots * \langle F^n \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)}. \]Proof. The first statement follows immediately from Lemmas 4.4(1) and 3.3(1).
By Lemmas 4.4(1) and 3.3(2), we have 
$\mathcal {E}_\mathsf {S} = \bigcup _{n \geqslant 1} (\mathsf {T})_n$, where 
$\mathsf {T} \mathrel {\mathop :}= \{F^n \mathsf {S} \mid n \in \mathbb {Z}\}$. Hence, for 
$D \in \mathcal {E}_\mathsf {S}$ there is a tower of the form
with 
$S_\ell \in \mathsf {S}$ for 
$1 \leqslant \ell \leqslant n$. By Corollary 4.5, we can re-order the indices in the tower above so that 
$i_1 \leqslant i_2 \leqslant \ldots \leqslant i_n$. Therefore, 
$\mathcal {E}_\mathsf {S} \subseteq \bigcup _{m< n} \langle F^m \mathsf {S} \rangle _{\mathsf {D}} * \langle F^{m+1} \mathsf {S} \rangle _{\mathsf {D}} * \cdots * \langle F^n \mathsf {S} \rangle _{\mathsf {D}}$, where 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$. The other inclusion is trivial.
Before we are able to prove Proposition 4.2, we need the following lemmas connecting the functorial finiteness of 
$\mathcal {E}_\mathsf {S}$ in 
$\mathsf {D}^b({\mathbf {k}} Q)$ and the functorial finiteness of the extension closure of 
$\mathsf {S}$ in 
$\mathsf {C}_{-w}$.
Lemma 4.7 Let 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}$ be the natural projection functor. If 
$\mathsf {S}$ is an 
$\infty$-orthogonal collection of 
$\mathsf {D}^b({\mathbf {k}} Q)$ contained in 
$\mathcal {F}_{-w}$, then 
$\pi (\mathcal {E}_\mathsf {S}) = \langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$.
Proof. To see that 
$\pi (\mathcal {E}_\mathsf {S}) \subseteq \langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$, observe that, by Lemma 4.6, 
$D \in \mathcal {E}_\mathsf {S}$ admits a tower as in (1) with each 
$S_\ell \in \mathsf {S}$. As 
$\pi (F^{i_\ell } S_\ell ) = S_\ell \in \mathsf {S}$, applying 
$\pi$ to the tower above gives a filtration of 
$\pi (D)$ in 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$.
Conversely, we need to show that if 
$D \in \pi ^{-1}(\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}})$, then 
$D \in \mathcal {E}_\mathsf {S}$. It is enough to check for 
$D$ indecomposable. Let 
$D \in \pi ^{-1} (\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}})$ be indecomposable; note that 
$D \in F^k \mathcal {F}_{-w}$ for some 
$k \in \mathbb {Z}$. We proceed by induction on the 
$\mathsf {S}$-length of 
$\pi (D)$ in 
$\mathsf {C}_{-w}$. If 
$D \in \pi ^{-1} (\mathsf {S})$, then 
$D = F^k S$ for some 
$S \in \mathsf {S}$. Hence, 
$D \in \{F^i \mathsf {S} \mid i \in \mathbb {Z}\} \subseteq \mathcal {E}_\mathsf {S}$. Suppose 
$n > 1$. Assume, by induction, that if 
$D \in \pi ^{-1}(\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}})$ is such that 
$\pi (D)$ has 
$\mathsf {S}$-length 
$n-1$ in 
$\mathsf {C}_{-w}$, then 
$D \in \mathcal {E}_\mathsf {S}$ has 
$\{F^i \mathsf {S} \mid i \in \mathbb {Z}\}$-length 
$n-1$ in 
$\mathcal {E}_\mathsf {S}$. Now suppose 
$D \in \pi ^{-1}(\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}})$ is such that 
$\pi (D)$ has 
$\mathsf {S}$-length 
$n$ in 
$\mathsf {C}_{-w}$. Then, by Lemma 3.3(2), there is a triangle in 
$\mathsf {C}_{-w}$ of the form
\[ C\rightarrow \pi(D)\rightarrow S\rightarrow \Sigma C, \]
with 
$S \in \mathsf {S}$ and 
$C \in \langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$ has 
$\mathsf {S}$-length 
$n-1$ in 
$\mathsf {C}_{-w}$. This triangle is the image under 
$\pi$ of a triangle in 
$\mathsf {D}^b({\mathbf {k}} Q)$ of the form
\[ F^i D'\rightarrow D\rightarrow F^j S\rightarrow \Sigma F^i D', \]
where 
$i \in \{k, k-1\}$ and 
$j \in \{k, k+1\}$, by Lemma 1.4. As 
$\pi (F^i D') = C$, it follows by induction that 
$F^i D' \in \mathcal {E}_\mathsf {S}$ has 
$\{F^i \mathsf {S} \mid i \in \mathbb {Z}\}$-length 
$n-1$ in 
$\mathsf {D}^b({\mathbf {k}} Q)$, whence 
$D \in \mathcal {E}_\mathsf {S}$ has 
$\{F^i \mathsf {S} \mid i \in \mathbb {Z}\}$-length 
$n$.
Lemma 4.8 Let 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}$ be the natural projection functor. Suppose 
$\mathsf {S}$ is an 
$\infty$-orthogonal collection of 
$\mathsf {D}^b({\mathbf {k}} Q)$ contained in 
$\mathcal {F}_{-w}$. Then 
$\mathcal {E}_\mathsf {S}$ is contravariantly (respectively, covariantly, functorially) finite in 
$\mathsf {D}^b({\mathbf {k}} Q)$ if and only if 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$ is contravariantly (respectively, covariantly, functorially) finite in 
$\mathsf {C}_{-w}$.
Proof. We only establish the contravariantly finite statements; the covariantly finite statement is similar and the functorially finite statement follows from combining both.
Suppose 
$\mathcal {E}_\mathsf {S}$ is contravariantly finite in 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$. For 
$D \in \mathcal {F}_{-w}$, take a minimal right 
$\mathcal {E}_\mathsf {S}$-approximation of 
$D$ in 
$\mathsf {D}$ and extend it to a triangle,
\[ E_D\stackrel{\alpha}{\longrightarrow} D\longrightarrow X_D\longrightarrow \Sigma E_D. \]
By the triangulated Wakamatsu lemma (see, e.g., [Reference JørgensenJør09, Lemma 2.1]), 
$X_D \in (\mathcal {E}_\mathsf {S})^\perp$. Applying 
$\pi$ to this triangle, we get the following triangle in 
$\mathsf {C}_{-w}$:
\[ \pi(E_D)\stackrel{\pi(\alpha)}{\longrightarrow} \pi(D)\longrightarrow \pi(X_D)\longrightarrow \Sigma \pi(E_D). \]
By Lemma 4.7, we have 
$\pi (E_D) \in \langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$. By construction of 
$\mathsf {C}_{-w}$, see § 1.2, we have 
$\mathsf {Hom}_{\mathsf {C}_{-w}} (\mathsf {S}, \pi (X_D)) = \bigoplus _{i \in \mathbb {Z}} \mathsf {Hom}_\mathsf {D} (F^i \mathsf {S}, X_D) = 0$ because 
$X_D \in (\mathcal {E}_\mathsf {S})^\perp$. Therefore, 
$\pi (\alpha )$ is a right 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$-approximation of 
$D = \pi (D)$, and so 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$ is contravariantly finite in 
$\mathsf {C}_{-w}$.
Conversely, suppose 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$ is contravariantly finite in 
$\mathsf {C}_{-w}$. Let 
$D \in \mathsf {D}$ and consider the extension of a minimal right 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$-approximation of 
$\pi (D)$ to a triangle in 
$\mathsf {C}_{-w}$,
\[ S_D\stackrel{}{\longrightarrow} \pi(D)\longrightarrow Y_D\longrightarrow \Sigma S_D, \]
where 
$\mathsf {Hom}_{\mathsf {C}_{-w}} (\mathsf {S}, Y_D) = 0$ by the triangulated Wakamatsu lemma. As the triangulated structure on 
$\mathsf {C}_{-w}$ is induced by that of 
$\mathsf {D}$, this triangle is the image under 
$\pi$ of a triangle,
\[ E_D\stackrel{f}{\longrightarrow} D\longrightarrow X_D\longrightarrow \Sigma E_D \]
in 
$\mathsf {D}$. It follows from Lemma 4.7 that 
$E_D \in \mathcal {E}_\mathsf {S}$. On the other hand, we have 
$0 = \mathsf {Hom}_{\mathsf {C}_{-w}}(\mathsf {S}, Y_D) = \bigoplus _{i \in \mathbb {Z}} \mathsf {Hom}_\mathsf {D}(F^i \mathsf {S}, X_D)$. Hence, 
$\mathsf {Hom}_\mathsf {D} (F^i \mathsf {S}, X_D) = 0$, for all 
$i \in \mathbb {Z}$, and so 
$X_D \in (\mathcal {E}_\mathsf {S})^\perp$. Therefore, the map 
$f$ is a right 
$\mathcal {E}_\mathsf {S}$-approximation of 
$D$, from which it follows that 
$\mathcal {E}_\mathsf {S}$ is contravariantly finite in 
$\mathsf {D}$.
We are almost ready to prove Proposition 4.2. First, we set up a final piece of notation. For integers 
$m \leqslant n$ and an 
$\infty$-orthogonal collection 
$\mathsf {S}$, we set
\[ \mathcal{E}_\mathsf{S}^{[m,n]} \mathrel{\mathop:}= \langle F^m \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} * \langle F^{m+1} \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} * \cdots * \langle F^n \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} \subseteq \mathcal{E}_\mathsf{S}. \]Proof Proof of Proposition 4.2
Let 
$\mathsf {S}$ be a simple-minded collection in 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$ contained in 
$\mathcal {F}_w$. By the dual of [Reference Iyama and JinIJ20, Proposition 3.6], 
$\pi (\mathsf {S})$ is a left 
$w$-Riedtmann configuration in 
$\mathsf {C}_{-w}$. Hence, by Proposition 3.5, it only remains to check that 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$ is contravariantly finite in 
$\mathsf {C}_{-w}$. Hence, by Lemma 4.8, it suffices to show that 
$\mathcal {E}_\mathsf {S}$ is contravariantly finite in 
$\mathsf {D}$.
Let 
$D \in \mathsf {D}$. There are only finitely many 
$i \in \mathbb {Z}$ with 
$\mathsf {Hom}_{\mathsf {D}} (F^i \mathsf {S},D) \neq 0$ as 
${\mathbf {k}} Q$ is hereditary. Let 
$m, n \in \mathbb {Z}$ be such that 
$m \leqslant n$ and 
$\mathsf {Hom}_{\mathsf {D}} (F^{< m} \mathsf {S}, D) = 0 = \mathsf {Hom}_{\mathsf {D}} (F^{>n} \mathsf {S},D)$. By Corollary 3.7, 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$ is contravariantly finite in 
$\mathsf {D}^b({\mathbf {k}} Q)$. Hence, 
$\mathcal {E}_\mathsf {S}^{[m,n]}$ is contravariantly finite in 
$\mathsf {D}^b({\mathbf {k}} Q)$ by [Reference Saorín and ZvonarevaSZ21, Lemma 5.3(1)]. As any component of a nonzero morphism from an object of 
$\mathcal {E}_\mathsf {S}$ to 
$D$ must originate from a summand 
$E \in \mathcal {E}_\mathsf {S}^{[m, n]}$, we have that any right 
$\mathcal {E}_\mathsf {S}^{[m,n]}$-approximation of 
$D$ is also a right 
$\mathcal {E}_\mathsf {S}$-approximation. Hence, 
$\mathcal {E}_\mathsf {S}$ is contravariantly finite in 
$\mathsf {D}$.
4.2 The induced map $\pi$ is surjective
In order to complete the proof of Theorem 4.1, we have to show that the map 
$\pi$ induced by the natural projection functor 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}$ in Proposition 4.2 is surjective. To see this, we need a lemma, which first requires some notation. For an 
$\infty$-orthogonal collection 
$\mathsf {S}$ in 
$\mathsf {D}^b({\mathbf {k}} Q)$ and an integer 
$n$, we define the following subcategories of 
$\mathcal {E}_\mathsf {S}$:
\[ \mathcal{E}_\mathsf{S}^{\leqslant n} \mathrel{\mathop:}= \bigcup_{i \leqslant n} \langle F^i \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} * \langle F^{i+1} \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} * \cdots * \langle F^n \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} \]and
\[ \mathcal{E}_\mathsf{S}^{\geqslant n} \mathrel{\mathop:}= \bigcup_{i \geqslant n} \langle F^n \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} * \langle F^{n+1} \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)} * \cdots * \langle F^i \mathsf{S} \rangle_{\mathsf{D}^b({\mathbf{k}} Q)}. \]
Similarly, we also set 
$\mathcal {E}_\mathsf {S}^{< n} = \mathcal {E}_\mathsf {S}^{\leqslant n-1}$ and 
$\mathcal {E}_\mathsf {S}^{> n} = \mathcal {E}_\mathsf {S}^{\geqslant n+1}$.
Lemma 4.9 Let 
$\mathsf {S}$ be an 
$\infty$-orthogonal collection in 
$\mathsf {D}^b({\mathbf {k}} Q)$. Then:
(1)
$\langle \mathsf {S} \rangle _{\mathsf {D}^b({\mathbf {k}} Q)}$ is contravariantly finite in $\mathcal {E}_\mathsf {S}^{\leqslant 0}$;(2)
$\langle \mathsf {S} \rangle _{\mathsf {D}^b({\mathbf {k}} Q)}$ is covariantly finite in $\mathcal {E}_\mathsf {S}^{\geqslant 0}$.
Proof. We only prove the first statement; the second statement is dual. Write 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$. Let 
$D \in \mathcal {E}_\mathsf {S}^{\leqslant 0}$. First, note that if 
$\mathsf {Hom}_{\mathsf {D}} (\mathsf {S}, D) = 0$, then 
$D$ admits a (minimal) right 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$-approximation, namely 
$S_D = 0 \longrightarrow D$, whose cone 
$X_D \simeq D \in \mathsf {S}^\perp$. Therefore, we may assume that 
$\mathsf {Hom}_{\mathsf {D}} (\mathsf {S},D) \neq 0$.
By Lemma 4.6, 
$d$ admits a decomposition,
\begin{equation} E^{{<}0}\stackrel{\alpha}{\longrightarrow} D\stackrel{\beta}{\longrightarrow} E^0\stackrel{}{\longrightarrow} \Sigma E^{{<}0}, \end{equation}
with 
$E^{<0} \in \mathcal {E}_\mathsf {S}^{<0}$ and 
$E^0 \in \langle \mathsf {S} \rangle _{\mathsf {D}}$. We shall construct a right 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$-approximation of 
$D$ by induction on the 
$\mathsf {S}$-length of 
$E^0$ in 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$.
Suppose the 
$\mathsf {S}$-length of 
$E^0$ is one, i.e. 
$E^0 \in \mathsf {S}$, and suppose 
$\varphi \colon S \longrightarrow D$ is a nonzero map with 
$S \in \mathsf {S}$. If 
$\beta \varphi = 0$, then 
$\varphi = 0$ because it factors through 
$E^{<0}$ and, by Lemma 4.4, 
${\mathsf {Hom}_{\mathsf {D}} (\mathsf {S}, E^{<0}) = 0}$. Hence, 
$\beta \varphi \neq 0$, and because 
$S, E^0 \in \mathsf {S}$, 
$\beta \varphi$ must be an isomorphism because 
$\mathsf {S}$ is an orthogonal collection in 
$\mathsf {D}$. Therefore, 
$\beta$ is a split epimorphism and 
$D \simeq E^0 \oplus E^{<0}$. It follows that 
$S \simeq E^0$ is the unique 
$S \in \mathsf {S}$, up to isomorphism, such that 
$\mathsf {Hom}_{\mathsf {D}}(S,D) \neq 0$. Hence, 
$E^0 \stackrel {[\begin {smallmatrix} 1 \\ 0 \end {smallmatrix}]}{\longrightarrow } D$ is a right 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$-approximation of 
$D$, whose cone 
$X_D = E^{<0} \in \mathsf {S}^\perp$.
Now suppose the 
$\mathsf {S}$-length of 
$E^0$ is 
$n >1$, i.e. there is a triangle 
$S'\rightarrow E^0\rightarrow S\rightarrow \Sigma S'$ with 
$S \in \mathsf {S}$, and 
$S' \in \langle \mathsf {S} \rangle _{\mathsf {D}}$ of 
$\mathsf {S}$-length 
$n-1$. Combining this triangle with (2), we obtain the following octahedral diagram.
The right-hand vertical triangle gives a decomposition of 
$A$ in 
$\mathcal {E}_\mathsf {S}^{\leqslant 0}$, 
$E^{<0}\rightarrow A\rightarrow S'\rightarrow \Sigma E^{<0}$, in which the 
$\mathsf {S}$-length of 
$S'$ is 
$n-1$. Hence, by induction, 
$A$ admits a right 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$-approximation 
$S_A \longrightarrow A$, whose cone 
$X_A$ lies in 
$\mathsf {S}^\perp$. Consider the following octahedral diagram.
If 
$Y \in \mathsf {S}^\perp$, then 
$\alpha$ is a right 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$-approximation of 
$D$ with cone lying in 
$\mathsf {S}^\perp$, and we are done. Thus, suppose 
$Y \not \in \mathsf {S}^\perp$. For 
$S_1 \in \mathsf {S}$, applying 
$\mathsf {Hom}_{\mathsf {D}} (S_1, -)$ to the right-hand vertical triangle in (
), shows that the map 
$\mathsf {Hom}_{\mathsf {D}} (S_1, \beta ) \colon \mathsf {Hom}_{\mathsf {D}} (S_1,Y) \hookrightarrow \mathsf {Hom}_{\mathsf {D}} (S_1,S)$ is injective because 
$X_A \in \mathsf {S}^\perp$. Hence, if 
$S_1 \neq S$, then 
$\mathsf {Hom}_{\mathsf {D}} (S_1, Y) = 0$. As 
$Y \not \in \mathsf {S}^\perp$, it follows that we must have 
$\mathsf {Hom}_{\mathsf {D}} (S,Y) \neq 0$ and 
$\mathsf {Hom}_{\mathsf {D}} (S,\beta )$ is injective. Suppose 
$\gamma \in \mathsf {Hom}_{\mathsf {D}} (S, Y)$ is nonzero. Then 
$\beta \gamma$ must be an isomorphism, which implies that 
$\beta$ is a split epimorphism, whence 
$Y \simeq S \oplus X_A$.
Now, using the other split triangle, we obtain the following new octahedral diagram.
Clearly, 
$S_D \in \langle \mathsf {S} \rangle _{\mathsf {D}}$, and because 
$X_A \in \mathsf {S}^\perp$, 
$g$ is a right 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$-approximation of 
$D$ with cone in 
$\mathsf {S}^\perp$. This finishes the proof.
We are now ready to prove Theorem 4.1.
Proof Proof of Theorem 4.1
By Proposition 4.2, the map 
$\pi$ is well defined and it is clearly injective because the projection functor 
$\pi$ gives a bijection between 
$\mathsf {ind}(\mathcal {F}_{-w})$ and 
$\mathsf {ind}(\mathsf {C}_{-w})$. It remains to show that 
$\pi$ induces a surjection.
Let 
$\mathsf {S}$ be a 
$w$-simple-minded system in 
$\mathsf {C}_{-w}$. The fact that the lift of 
$\mathsf {S}$ to 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$, which will also be denoted by 
$\mathsf {S}$, is an 
$\infty$-orthogonal collection in 
$\mathsf {D}$ follows from the proof of [Reference Iyama and JinIJ20, Theorem 1.2], as this part of the proof does not require 
$Q$ to be Dynkin. Hence, it remains to show that 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {S}) = \mathsf {D}$.
First, we claim that 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$ is functorially finite in 
$\mathcal {E}_\mathsf {S}$. Indeed, on the one hand, we have that 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$ is contravariantly finite in 
$\mathcal {E}_\mathsf {S}^{\leqslant 0}$ by Lemma 4.9. On the other hand, because 
$\mathcal {E}_\mathsf {S} = \mathcal {E}_\mathsf {S}^{\leqslant 0} * \mathcal {E}_\mathsf {S}^{>0}$ by Lemma 4.6, and 
$\{F^n \mathsf {S} \mid n \in \mathbb {Z}\}$ is an orthogonal collection in 
$\mathsf {D}$, we have that 
$\mathcal {E}_\mathsf {S}^{\leqslant 0}$ is contravariantly finite in 
$\mathcal {E}_\mathsf {S}$. Hence, by transitivity, 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$ is contravariantly finite in 
$\mathcal {E}_\mathsf {S}$. Dually, using 
$\mathcal {E}_\mathsf {S}^{\geqslant 0}$, 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$ is also covariantly finite in 
$\mathcal {E}_\mathsf {S}$, and therefore 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$ is functorially finite in 
$\mathcal {E}_\mathsf {S}$. As 
$\mathsf {S}$ is a 
$w$-simple-minded system in 
$\mathsf {C}_{-w}$, we have that 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$ is functorially finite in 
$\mathsf {C}_{-w}$. It then follows by Lemma 4.8 and transitivity that 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$ is functorially finite in 
$\mathsf {D}$.
We now show that 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {S}) = \mathsf {D}$. As 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$ is functorially finite in 
$\mathsf {D}$, we have that 
$\langle \mathsf {S} \rangle _{\mathsf {D}}$ is contravariantly finite in 
$(\Sigma ^{> 0} \mathsf {S})^\perp$ and covariantly finite in 
${}^\perp (\Sigma ^{<0} \mathsf {S})$. As 
${\mathbf {k}} Q$ is hereditary, for any 
$D \in \mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$, we have 
$\mathsf {Hom}_{\mathsf {D}}(\Sigma ^i D, \mathsf {S}) = 0 = \mathsf {Hom}_{\mathsf {D}}(\Sigma ^i \mathsf {S}, D)$ for 
$i \gg 0$. Therefore, by [Reference JinJin19, Proposition 3.2], we have that 
$({}^\perp (\Sigma ^{<0} \mathsf {S}),\mathsf {cosusp}\ \mathsf {S})$ is a t-structure in 
$\mathsf {D}$.
Without loss of generality, we may assume that 
$0 \neq D \in \langle \Sigma ^{\leqslant -w-2}\mathsf{mod}({{\mathbf {k}} Q}) \rangle _{\mathsf {D}}$. As a consequence, 
$\mathsf {Hom}_{\mathsf {D}}(D, \Sigma ^{\geqslant 0} \mathsf {S}) = 0$. Consider the decomposition triangle of 
$D$ with respect to the t-structure 
$({}^\perp (\Sigma ^{<0} \mathsf {S}),\mathsf {cosusp}\ \mathsf {S})$:
\[ X_D\rightarrow D\rightarrow Y_D\rightarrow \Sigma X_D. \]
The morphism 
$X_D \to D$ is, thus, a minimal right 
${}^\perp (\Sigma ^{<0} \mathsf {S})$-approximation, which is therefore zero if and only if 
$X_D \simeq 0$. Suppose 
$X_D \neq 0$, then the morphism 
$X_D \to D$ must be nonzero. As 
${\mathbf {k}} Q$ is hereditary, this means that 
$X_D \in \langle \Sigma ^{\leqslant -w-2} \mathsf{mod}({{\mathbf {k}} Q}) \rangle _{\mathsf {D}}$ also, in which case 
${\mathsf {Hom}_{\mathsf {D}}(X_D, \Sigma ^{\geqslant 0} \mathsf {S}) = 0}$. Hence, 
$X_D \in {}^\perp (\Sigma ^{\mathbb {Z}} \mathsf {S})$. Now, by the final part of the proof of [Reference Iyama and JinIJ20, Theorem 1.2], we can conclude that 
$X_D \simeq 0$. Hence,
$D \simeq Y_D \in \mathsf {cosusp}\ \mathsf {S} \subseteq \mathsf {thick}_{\mathsf {S}}(\mathsf {D})$. It follows that 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {S}) = \mathsf {D}$, as required.
5. Sincere orthogonal collections
Let 
$Q$ be an acyclic quiver. In this section, we establish a bijection between 
$w$-simple-minded systems in 
$\mathsf {C}_{-w}({\mathbf {k}} Q)$ and sincere 
$\infty$-orthogonal collections of 
$\mathsf {D}^b({\mathbf {k}} Q)$ sitting in some truncation of the fundamental domain of 
$\mathsf {C}_{-w}({\mathbf {k}} Q)$; see Theorem 5.8. This result generalises [Reference Coelho SimõesCoe12, Theorem 4.8], which established the same result in the case that 
$w=1$ and 
$Q$ is simply laced Dynkin. In § 6, we use Theorem 5.8 to establish a bijection between 
$w$-simple-minded systems and positive 
$w$-noncrossing partitions in the Weyl group of the corresponding type. However, we believe that Theorem 5.8 holds independent representation-theoretic interest.
Before proceeding, we require some background on exceptional sequences.
5.1 Exceptional sequences
The notion of exceptional sequence goes back to the Moscow school in the 1980s; see, e.g., [Reference RudakovRud90]. Recall from [Reference BondalBon90] that an object 
$e$ in a triangulated category 
$\mathsf {D}$ is called exceptional if 
$\mathsf {Hom}_\mathsf {D}(e, \Sigma ^i e) = 0$ for all 
$i \neq 0$ and 
$\mathsf {Hom}_\mathsf {D}(e,e) \simeq {\mathbf {k}}$. An ordered collection of exceptional objects 
$\mathsf {E} = (e_1,\ldots,e_r)$ of 
$\mathsf {D}$ is called an exceptional sequence if 
$\mathsf {Hom}_\mathsf {D}(e_j, \Sigma ^i e_k) = 0$ for all 
$i \in \mathbb {Z}$ and 
$j > k$. The exceptional sequence 
$\mathsf {E}$ is called complete if 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {E}) = \mathsf {D}$. If 
$Q$ is an acyclic quiver with 
$n$ vertices and 
$\mathsf {E} = (E_1,\ldots,E_r)$ is an exceptional sequence in 
$\mathsf {D}^b({\mathbf {k}} Q)$ then 
$\mathsf {E}$ is complete if and only if 
$r = n$; see [Reference Buan, Reiten and ThomasBRT12, Reference Crawley-BoeveyCra93, Reference RingelRin94].
Exceptional sequences are often called ‘exceptional collections’. In this article, we avoid this term to avoid ambiguity when considering orthogonal collections.
The following lemma gives a link between exceptional sequences and simple-minded collections in 
$\mathsf {D}^b({\mathbf {k}} Q)$.
Lemma 5.1 Let 
$Q$ be an acyclic quiver with 
$n$ vertices. If 
$\mathsf {S}$ is a simple-minded collection in 
$\mathsf {D}^b({\mathbf {k}} Q)$ then the objects of 
$\mathsf {S}$ can be ordered into a (complete) exceptional sequence 
$\mathsf {E} = (E_1,\ldots,E_n)$ in which the cohomological degrees of the 
$E_i$ are weakly decreasing.
Proof. By [Reference Buan, Reiten and ThomasBRT12, Lemma 2.3], the objects of a 
$\mathsf {Hom}_{\leqslant 0}$-configuration (for the definition, see [Reference Buan, Reiten and ThomasBRT12, § 2.2]) can be ordered into a complete exceptional sequence 
$\mathsf {E} = (E_1,\ldots,E_n)$ in which the cohomological degrees of the 
$E_i$ are weakly decreasing, and therefore strongly generate 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$. Hence, the set of 
$\mathsf {Hom}_{\leqslant 0}$-configurations in 
$\mathsf {D}$ is a subset of the set of simple-minded collections. By [Reference Buan, Reiten and ThomasBRT12, Theorem 2.4], the set of 
$\mathsf {Hom}_{\leqslant 0}$-configurations in 
$\mathsf {D}$ is in bijection with the set of silting objects in 
$\mathsf {D}$. However, the map from the set of 
$\mathsf {Hom}_{\leqslant 0}$-configurations in 
$\mathsf {D}$ to the set of silting objects in 
$\mathsf {D}$ constructed in [Reference Buan, Reiten and ThomasBRT12] coincides with the map from simple-minded collections in 
$\mathsf {D}$ to silting objects in 
$\mathsf {D}$; see [Reference Koenig and YangKY14, § 5.6]. Hence the set of 
$\mathsf {Hom}_{\leqslant 0}$-configurations in 
$\mathsf {D}$ coincides with the set of simple-minded collections in 
$\mathsf {D}$, giving the lemma.
5.2 Sincere orthogonal collections
Let 
$Q$ be an acyclic quiver and 
$w \geqslant 1$ be an integer. Write 
$\mathsf {H} \mathrel {\mathop :}= \mathsf{mod}({{\mathbf {k}} Q})$ and consider the functor
\begin{equation} H \colon \mathsf{D}^b({\mathbf{k}} Q) \longrightarrow \mathsf{H} \text{ given by } X \longmapsto \bigoplus_{i \in \mathbb{Z}} H^i(X), \end{equation}
where 
$H^i(-)$ denotes the 
$i$th cohomology of 
$X$ with respect to the standard t-structure 
$(\mathsf {X},\mathsf {Y})$ in 
$\mathsf {D}^b({\mathbf {k}} Q)$.
Recall that a module 
$M \in \mathsf {H}$ is called sincere if 
$\mathsf {Hom}_\mathsf {H}(P,M) \neq 0$ for any projective module 
$P$. A set of modules 
$\mathsf {X} \subseteq \mathsf {H}$ will be called a sincere set of modules if for each projective module 
$P$ there exists a module 
$X \in \mathsf {X}$ such that 
$\mathsf {Hom}_\mathsf {H}(P,X) \neq 0$. If 
$\mathsf {X}$ is a finite set, then 
$\mathsf {X}$ is a sincere set of modules if and only if 
$\bigoplus _{X \in \mathsf {X}} X$ is a sincere module. Note that there are equivalent formulations of sincerity using injective modules. Using sincerity, we make the following definition.
Definition 5.2 An 
$\infty$-orthogonal collection 
$\mathsf {S} \subseteq \mathsf {D}^b({\mathbf {k}} Q)$ will be called 
$w$-sincere if 
$\mathsf {S} \subseteq \mathsf {X} \cap \Sigma ^w \mathsf {Y} \subseteq \mathcal {F}_{-w}$ and 
$\{H(S) \mid S \in \mathsf {S}\}$ is a sincere set of modules in 
$\mathsf {H}$. It will be called exceptionally finite if the objects of 
$\mathsf {S}$ can be ordered into an exceptional sequence and 
$\langle \mathsf {S} \rangle _{\mathsf {D}^b({\mathbf {k}} Q)}$ is functorially finite in 
$\mathsf {D}^b({\mathbf {k}} Q)$.
Recall 
$\pi \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf {C}_{-w}$ is the canonical projection functor.
Proposition 5.3 Let 
$Q$ be an acyclic quiver and 
$w \geqslant 1$ an integer. Then there is a well-defined map
\begin{align*} \Theta \colon \Big\{ \begin{matrix} w\textrm{-Riedtmann configurations}\\ \textrm{in}\ \mathsf{C}_{{-}w}\end{matrix} \Big\} & \longrightarrow \Big\{ \begin{matrix} w\textrm{-sincere}\ \infty\,\textrm{-orthogonal}\\ \textrm{collections in}\ \mathsf{D}^b({\mathbf{k}} Q)\end{matrix} \Big\}, \\ \mathsf{S} & \longmapsto \pi^{{-}1}(\mathsf{S}) \cap \mathsf{X} \cap \Sigma^w \mathsf{Y} \end{align*}which restricts to a well-defined map
\[ \Theta \colon \Big\{ \begin{matrix} w\textrm{-simple-minded}\\ \textrm{systems in}\ \mathsf{C}_{{-}w}\end{matrix} \Big\} \longrightarrow \Big\{ \begin{matrix} \textrm{exceptionally finite},\ w\textrm{-sincere}\ \infty\textrm{-orthogonal}\\ \textrm{collections in}\ \mathsf{D}^b({\mathbf{k}}\textit{Q)}\end{matrix} \Big\}. \]Proof. Let 
$\mathsf {S}$ be a 
$w$-Riedtmann configuration in 
$\mathsf {C}_{-w}$. Partition the lift of 
$\mathsf {S}$ into 
$\mathcal {F}_{-w}$, 
$\pi ^{-1}(\mathsf {S}) \cap \mathcal {F}_{-w}$, into 
$\mathsf {R} \cup \mathsf {T}$, where 
$\mathsf {R} \subseteq \mathsf {X} \cap \Sigma ^w \mathsf {Y}$ and 
$\mathsf {T} \subseteq \Sigma ^w \mathsf {X} \cap \mathbb {S} \Sigma ^w \mathsf {Y}$. We need to show that 
$\mathsf {R}$ is a 
$w$-sincere 
$\infty$-orthogonal configuration. As in the proof of Theorem 4.1, we can invoke [Reference Iyama and JinIJ20, Theorem 1.2] to see that 
$\mathsf {R}$ is 
$\infty$-orthogonal. By definition, 
$\mathsf {R} \subseteq \mathsf {X} \cap \Sigma ^w \mathsf {Y}$, so it only remains to show the sincerity part of the definition.
Suppose, for a contradiction, that 
$\{H(R) \mid R \in \mathsf {R}\}$ is not a sincere set. This means that there exists an indecomposable projective module 
$P$ such that 
$\mathsf {Hom}_{\mathsf {D}}(P, \Sigma ^{-i} R) = 0$ for each 
$R \in \mathsf {R}$ and 
$0 \leqslant i \leqslant w-1$, where 
$\mathsf {D} = \mathsf {D}^b ({\mathbf {k}} Q)$. Now, because 
$P \in \mathcal {F}_{-w}$ and 
$\mathsf {R} \subseteq \mathcal {F}_{-w}$, by Lemma 1.4 for 
$0 \leqslant i \leqslant w-1$, we have
\begin{align*} \mathsf{Hom}_{\mathsf{C}_{{-}w}}(P,\Sigma^{{-}i}R) & \simeq \mathsf{Hom}_{\mathsf{D}}(P,\Sigma^{{-}i} R) \oplus D\, \mathsf{Hom}_{\mathsf{D}}(R, \Sigma^{i-w} P) \\ & \simeq D\, \mathsf{Hom}_{\mathsf{D}}(R, \Sigma^{i-w} P). \end{align*}
As 
$i - w < 0$ for each 
$i$, 
$\mathsf {R} \subseteq \mathcal {F}_{-w}$ and 
$P \in \mathsf {H}$, the hereditary property means that 
$\mathsf {Hom}_{\mathsf {D}}(R, \Sigma ^{i-w} P) = 0$. Hence, 
$\mathsf {Hom}_{\mathsf {C}_{-w}}(P,\Sigma ^{-i}R) = 0$ for each 
$R \in \mathsf {R}$ and each 
$0 \leqslant i \leqslant w-1$.
Now each 
$T \in \mathsf {T}$ can be written as 
$T = \Sigma ^w T'$ for some 
$T' \in \mathsf {H}$. Again, using Lemma 1.4, for 
$0 \leqslant i \leqslant w-1$, we have
\begin{align*} \mathsf{Hom}_{\mathsf{C}_{{-}w}}(P,\Sigma^{{-}i} T) & \simeq \mathsf{Hom}_{\mathsf{D}}(P, \Sigma^{{-}i} T) \oplus D\, \mathsf{Hom}_{\mathsf{D}}(T, \Sigma^{i-w} P) \\ & \simeq \mathsf{Hom}_{\mathsf{D}}(P, \Sigma^{w-i} T') \oplus D\, \mathsf{Hom}_{\mathsf{D}}(T', \Sigma^{i-2w} P). \end{align*}
As 
$w - i \geqslant 1$ and 
$P$ is projective, we have 
$\mathsf {Hom}_{\mathsf {D}}(P, \Sigma ^{w-i} T') =0$. As 
$i - 2w < 0$, and 
$\mathsf {H}$ is hereditary, we have 
$\mathsf {Hom}_{\mathsf {D}}(T', \Sigma ^{i-2w} P) = 0$. It follows that 
$\mathsf {Hom}_{\mathsf {C}_{-w}}(P,\Sigma ^{-i} T) = 0$ for each 
$0 \leqslant i \leqslant w-1$ and 
$T \in \mathsf {T}$. As 
$0 \neq P \in \mathsf {C}_{-w}$, this contradicts the fact that 
$\mathsf {S}$ is a 
$w$-Riedtmann configuration. Hence, 
$\{H(R) \mid R \in \mathsf {R}\}$ must be a sincere set, as required.
Finally, to see the restriction, suppose further that 
$\mathsf {S}$ is a 
$w$-simple-minded system in 
$\mathsf {C}_{-w}$. Then 
$\langle \mathsf {R} \rangle _{\mathsf {C}_{-w}}$ is functorially finite in 
$\langle \mathsf {S} \rangle _{\mathsf {C}_{-w}}$ by Lemma 3.3
$(3)$. Hence, by Proposition 3.5 and transitivity of functorial finiteness, 
$\langle \mathsf {R} \rangle _{\mathsf {C}_{-w}}$ is functorially finite in 
$\mathsf {C}_{-w}$. By Lemmas 4.8 and 4.9, we see that 
$\langle \mathsf {R} \rangle _{\mathsf {D}}$ is functorially finite in 
$\mathsf {D}$. By Theorem 4.1 and Lemma 5.1, the objects of 
$\mathsf {S}$ and, hence, 
$\mathsf {R}$ can be ordered into an exceptional sequence, making 
$\mathsf {R}$ exceptionally finite, as required.
Putting together Proposition 5.3 with Theorem 4.1 we obtain the following corollary.
Corollary 5.4 Let 
$Q$ be an acyclic quiver and 
$w \geqslant 1$ an integer. Then there is a well-defined map
\begin{align*} \Theta \colon \Big\{\begin{matrix} \textrm{simple-minded collections of}\\ \mathsf{D}^b({\mathbf{k}}\,Q)\ \textrm{contained in}\ \mathcal{F}_{{-}w}\end{matrix}\Big\} & \longrightarrow \Big\{\begin{matrix} \textrm{exceptionally finite},\ w\textrm{-sincere}\ \infty\textrm{-orthogonal}\\ \textrm{collections in}\ \mathsf{D}^b({\mathbf{k}} Q)\end{matrix}\Big\}. \\ \mathsf{S} & \longmapsto \mathsf{S} \cap \mathsf{X} \cap \Sigma^w \mathsf{Y} \end{align*} We now aim to show that the map 
$\Theta$ defined in Corollary 5.4 is a bijection. In order to establish this we need a special case of Jin's reduction of simple-minded collections [Reference JinJin19, Theorem 3.1].
5.3 Reduction of simple-minded collections
In this section, we present an explicit specialisation of [Reference JinJin19, Theorem 3.1]. The following statement is related to [Reference JinJin19, Theorem 3.1] in a way analogous to the way that Aihara–Iyama's silting reduction theorem [Reference Aihara and IyamaAI12, Theorem 2.37] is related to Iyama–Yang's silting reduction theorem [Reference Iyama and YangIY18, Theorem 3.7]. We include a proof for the convenience of the reader.
Proposition 5.5 (Specialisation of [Reference JinJin19, Theorem 3.1])
Let 
$\mathsf {D}$ be a Hom-finite, Krull–Schmidt, 
${\mathbf {k}}$-linear triangulated category. Suppose 
$\mathsf {T}$ is an 
$\infty$-orthogonal collection such that 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {T})$ is functorially finite in 
$\mathsf {D}$. Then there is a bijection
\[ \Phi \colon \Big\{\begin{matrix} \textrm{simple-minded collections in}\\ \mathsf{D}\ \textrm{containing}\ \mathsf{T}\end{matrix} \Big\} \stackrel{1-1}{\longrightarrow} \Big\{\begin{matrix} \textrm{simple-minded collections}\\ \textrm{in}\ (\Sigma^{\mathbb{Z}} \mathsf{T})^\perp\end{matrix}\Big\}. \] In Appendix A we include another proof which does not rely on the functorial finiteness of the subcategory generated by 
$\mathsf {T}$ or use Verdier localisation.
Proof. The following argument is analogous to [Reference Aihara and IyamaAI12, Theorem 2.37].
Let 
$\mathsf {S}$ be a simple-minded collection in 
$\mathsf {D}$ containing 
$\mathsf {T}$. For each 
$s \in \mathsf {S}$, consider the truncation triangle coming from the stable t-structure 
$(\mathsf {thick}_{\mathsf {D}}(\mathsf {T}), (\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp )$,
\begin{equation} t_s\rightarrow s\rightarrow Ls\rightarrow \Sigma t_s, \end{equation}
where 
$L \colon \mathsf {D} \to (\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp$ is the left adjoint to the inclusion 
$(\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp \hookrightarrow \mathsf {D}$. Define 
$\Phi (\mathsf {S}) \mathrel {\mathop :}= \mathsf {R} = \{ Ls \mid s \in \mathsf {S}\}$. Note that 
$Ls \neq 0$ if and only if 
$s \in \mathsf {S} \setminus \mathsf {T}$. By truncating 
$t_s$ with respect to the bounded t-structure 
$(\mathsf {susp}\ \mathsf {T},\mathsf {cosusp}\ \Sigma ^{-1}\mathsf {T})$ in 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {T})$, observe that the left 
$(\mathsf {cosusp}\ \Sigma ^{-1}\mathsf {T})$-approximation of 
$t_s$ in 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {T})$ also gives rise to a right 
$(\mathsf {thick}_{\mathsf {D}}(\mathsf {T}))$-approximation of 
$s$, which shows that 
$t_s \in \mathsf {cosusp}\ \Sigma ^{-1} \mathsf {T}$. Take 
$s_1,s_2 \in \mathsf {S}$ and consider the corresponding truncation triangle 
$t_i\rightarrow s_i\rightarrow Ls_i\rightarrow \Sigma t_i$ for 
$i = 1,2$. Applying the functor 
$\mathsf {Hom}_\mathsf {D}(-,Ls_2)$ to the truncation triangle for 
$s_1$ and the functor 
$\mathsf {Hom}_\mathsf {D}(s_1,-)$ to the truncation triangle for 
$s_2$ shows that 
$\mathsf {R}$ is an 
$\infty$-orthogonal collection in 
$(\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp$; here it is important to use the fact that 
$t_i \in \mathsf {cosusp}\ \Sigma ^{-1} \mathsf {T}$.
Suppose 
$d \in (\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp$. As 
$\mathsf {S}$ is a simple-minded collection in 
$\mathsf {D}$, there are integers 
$n \geqslant m$ such that 
$d \in \Sigma ^n \langle \mathsf {S} \rangle _\mathsf {D} * \cdots * \Sigma ^m \langle \mathsf {S} \rangle _\mathsf {D}$. Applying the functor 
$L$ to the corresponding tower for 
$d$ shows that 
$d \in \Sigma ^n \langle \mathsf {R} \rangle _{(\Sigma ^{\mathbb {Z}}\mathsf {T})^\perp } * \cdots * \Sigma ^m \langle \mathsf {R} \rangle _{(\Sigma ^{\mathbb {Z}}\mathsf {T})^\perp }$. Hence, 
$(\Sigma ^{\mathbb {Z}}\mathsf {T})^\perp = \mathsf {thick}_{(\Sigma ^{\mathbb {Z}}\mathsf {T})^\perp }(\mathsf {R})$ and 
$\mathsf {R}$ is a simple-minded collection in 
$(\Sigma ^{\mathbb {Z}}\mathsf {T})^\perp$. This shows that the map 
$\Phi$ is well defined.
We now construct a map
\[ \Psi \colon \Big\{ \begin{matrix} \textrm{simple-minded collections}\\ \textrm{in}\ (\Sigma^{\mathbb{Z}} \mathsf{T})^\perp\end{matrix} \Big\} \longrightarrow \Big\{ \begin{matrix} \textrm{simple-minded collections}\\ \textrm{in}\ \mathsf{D}\ \textrm{containing}\ \mathsf{T}\end{matrix} \Big\}. \]
First note that 
$\mathsf {cosusp}\ \mathsf {T}$ is covariantly finite in 
$\mathsf {D}$ because 
$\mathsf {cosusp}\ \mathsf {T}$ is covariantly finite in 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {T})$, which is, in turn, functorially finite in 
$\mathsf {D}$. Hence, there is an (unbounded) t-structure 
$({}^\perp (\Sigma ^{\leqslant 0} \mathsf {T}),\mathsf {cosusp}\ \mathsf {T})$ in 
$\mathsf {D}$. Let 
$\mathsf {R}$ be a simple-minded collection in 
$(\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp$. For each 
$r \in \mathsf {R}$ take the truncation triangle with respect to the t-structure 
$({}^\perp (\Sigma ^{\leqslant 0} \mathsf {T}),\mathsf {cosusp}\ \mathsf {T})$,
\begin{equation} \Sigma^{{-}1} t_r \to s_r \to r \to t_r, \end{equation}
and set 
$\Psi (\mathsf {R}) = \mathsf {T} \cup \{s_r \mid r \in \mathsf {R}\}$. In a manner analogous to the previous argument, one can show that 
$\Psi (\mathsf {R})$ is an 
$\infty$-orthogonal collection in 
$\mathsf {D}$. For generation, take 
$d \in \mathsf {D}$ and truncate with respect to the stable t-structure 
$(\mathsf {thick}_{\mathsf {D}}(\mathsf {T}), (\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp )$,
\[ t_d\rightarrow d\rightarrow Ld\rightarrow \Sigma t_d, \]
and observe that 
$Ld \in \mathsf {thick}_{(\Sigma ^{\mathbb {Z}}\mathsf {T})^\perp }(\mathsf {R}) = \mathsf {thick}_{\mathsf {D}}(\mathsf {R})$. It follows immediately that 
$d \in \mathsf {thick}_{\mathsf {D}}(\Psi (\mathsf {R}))$, whence 
$\Phi (\mathsf {R})$ is a simple-minded collection in 
$\mathsf {D}$, showing that 
$\Psi$ is well defined.
Finally, to see that 
$\Phi$ and 
$\Psi$ are mutually inverse, applying 
$\mathsf {Hom}_\mathsf {D}(-,t)$ for 
$t \in \mathsf {cosusp}\ \mathsf {T}$ to (5) reveals that the morphism 
$Ls \to \Sigma t$ is a left 
$(\mathsf {cosusp}\ \mathsf {T})$-approximation of 
$Ls$, and applying 
$\mathsf {Hom}_\mathsf {D}(t,-)$ for 
$t \in \mathsf {thick}_{\mathsf {D}}(\mathsf {T})$ to (6) reveals that 
$\Sigma ^{-1} t_r \to s_r$ is a right 
$(\mathsf {thick}_{\mathsf {D}}(\mathsf {T}))$-approximation of 
$s_r$.
5.4 Bijectivity of $\Theta$
To establish the bijectivity of the map occurring in Corollary 5.4 we require a notion of perpendicular category for abelian categories which is compatible with that for derived categories. We recall the following from [Reference Geigle and LenzingGL91, Reference SchofieldSch91].
Definition 5.6 Let 
$\mathsf {H}$ be an abelian category and 
$\mathsf {E}$ a collection of objects in 
$\mathsf {H}$. We define the right perpendicular category of 
$\mathsf {E}$ by
\[ \mathsf{E}^{\perp_{\mathsf{H}}} \mathrel{\mathop:}= \{ X \in \mathsf{H} \mid \mathsf{Hom}_\mathsf{H}(\mathsf{E},X) = 0 = \mathsf{Ext}^1_\mathsf{H}(\mathsf{E},X) \}. \]
There is an analogous definition of left perpendicular category, 
${}^{\perp _{\mathsf {H}}} \mathsf {E}$.
Lemma 5.7 Let 
$Q$ be an acyclic quiver with 
$n$ vertices, 
$\mathsf {H} = \mathsf{mod}({{\mathbf {k}} Q})$ and 
$\mathsf {E} = \{E_1,\ldots,E_k\}$ be a collection of exceptional 
${\mathbf {k}} Q$-modules for 
$k \leqslant n$. Then 
$(\Sigma ^{\mathbb {Z}} \mathsf {E})^\perp$ is equivalent to 
$\mathsf {D}^b({\mathbf {k}} Q')$, where 
$Q'$ is an acyclic quiver with 
$n - k$ vertices such that 
$\mathsf {E}^{\perp _{\mathsf {H}}} \simeq \mathsf{mod} ({{\mathbf {k}} Q'})$. Moreover, 
$\mathsf {H} \cap (\Sigma ^{\mathbb {Z}} \mathsf {E})^\perp = \mathsf {E}^{\perp _{\mathsf {H}}}$.
Proof. Let 
$\mathsf {H} = \mathsf{mod}({{\mathbf {k}} Q})$ and 
$\mathsf {D} = \mathsf {D}^b ({\mathbf {k}} Q)$. For 
$X \in \mathsf {H}$, we have 
$\mathsf {Hom}_{\mathsf {D}}(\Sigma ^i \mathsf {E},X) = 0$ for all 
$i \in \mathbb {Z} \setminus \{-1,0\}$ because 
$\mathsf {E} \subseteq \mathsf {H}$ and 
$\mathsf {H}$ is hereditary. Therefore, for 
$X \in \mathsf {H}$ we have 
$X \in (\Sigma ^{\mathbb {Z}} \mathsf {E})^\perp$ if and only if 
$X \in \mathsf {E}^{\perp _{\mathsf {H}}}$. In particular, it follows that 
$\Sigma ^i \mathsf {H} \cap (\Sigma ^{\mathbb {Z}} \mathsf {E})^\perp = \Sigma ^i \mathsf {E}^{\perp _{\mathsf {H}}}$ for each 
$i \in \mathbb {Z}$. Now, by [Reference SchofieldSch91, Theorem 2.5], there is an equivalence of (abelian) categories 
$\mathsf {E}^{\perp _{\mathsf {H}}} \to \mathsf{mod}({{\mathbf {k}} Q'})$. As 
$\mathsf {H}$ is hereditary, each object in 
$\mathsf {D}$ decomposes into a direct sum of its cohomology, and thus this equivalence induces an equivalence of triangulated categories 
$(\Sigma ^{\mathbb {Z}} \mathsf {E})^\perp \to \mathsf {D}^b({\mathbf {k}} Q')$.
Theorem 5.8 Let 
$Q$ be an acyclic quiver with 
$n$ vertices and 
$w \geqslant 1$ an integer. Then there is a bijection
\begin{align*} \Theta \colon \Big\{\begin{matrix} \textrm{simple-minded collections of}\\ \mathsf{D}^b({\mathbf{k}}\, Q)\ \textrm{contained in}\ \mathcal{F}_{{-}w}\end{matrix} \Big\} & \stackrel{1-1}{\longrightarrow} \Big\{ \begin{matrix} \textrm{exceptionally finite},\ w\textrm{-sincere}\ \infty\textrm{-orthogonal}\\ \textrm{collections in}\ \mathsf{D}^b({\mathbf{k}}\, \textit{Q)}\end{matrix} \Big\} \\ \mathsf{S} & \longmapsto \mathsf{S} \cap \mathsf{X} \cap \Sigma^w \mathsf{Y}. \end{align*}Proof. The strategy of the proof is based on [Reference Coelho SimõesCoe12, § 4]. The map 
$\Theta$ is well defined by Corollary 5.4. We first show that 
$\Theta$ is surjective.
Let 
$\mathsf {T}=\{T_1,\ldots,T_k\}$ be an exceptionally finite, 
$w$-sincere 
$\infty$-orthogonal collection in 
$\mathsf {D} = \mathsf {D}^b({\mathbf {k}} Q)$. As the objects of 
$\mathsf {T}$ can be ordered into an exceptional sequence we have 
$k \leqslant n$. To see that 
$\Theta$ is surjective, we need to find a simple-minded collection 
$\mathsf {S}$ such that 
$\mathsf {T} \subseteq \mathsf {S}$ and 
$\mathsf {S} \setminus \mathsf {T} \subseteq \Sigma ^{w+1} (\mathsf {H} \setminus \mathsf {inj}(\mathsf {H}))$. Let 
$\mathsf {E} = H(\mathsf {T})$, where 
$H$ is the standard cohomology functor; see (4). By [Reference BondalBon90, Theorem 3.2], the subcategory 
$\mathsf {thick}_{\mathsf {D}}(\mathsf {T}) = \mathsf {thick}_{\mathsf {D}}(\mathsf {E})$ is functorially finite in 
$\mathsf {D}$. Hence, by Proposition 5.5, we are looking for simple-minded collections 
$\mathsf {R}$ in 
$(\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp = (\Sigma ^{\mathbb {Z}} \mathsf {E})^\perp$ such that 
$\Psi (\mathsf {R}) \setminus \mathsf {T} \subseteq \Sigma ^{w+1} (\mathsf {H} \setminus \mathsf {inj}(\mathsf {H}))$, where 
$\Psi$ is defined in the proof of Proposition 5.5.
Now, by Lemma 5.7, 
$(\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp \simeq \mathsf {D}^b({\mathbf {k}} Q')$ for some acyclic quiver 
$Q'$ with 
$n - k$ vertices. Let 
$\mathsf {R}'$ be the image of the set of simple 
${\mathbf {k}} Q'$-modules in 
$(\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp$ under the equivalence, and set 
$\mathsf {R} = \Sigma ^{w+1} \mathsf {R}'$. Again, by Lemma 5.7, 
$\mathsf {R} \subseteq \Sigma ^{w+1} \mathsf {H} \cap (\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp$. As 
$\mathsf {T} \subseteq \mathsf {X} \cap \Sigma ^w \mathsf {Y}$, by the hereditary property we have that the object 
$T_R$ in (6) is zero for each 
$R \in \mathsf {R}$, whence 
$S_R = E$ and 
$\Psi (\mathsf {R}) \setminus \mathsf {T} = \mathsf {R}$. Finally, because 
$\mathsf {T}$ is 
$w$-sincere, for each injective 
${\mathbf {k}} Q$-module 
$I$ we have 
$\mathsf {Hom}_{\mathsf {D}}(\mathsf {T},\Sigma ^{w+1}I) \neq 0$, whence for each 
$R \in \mathsf {R}$ we have 
$R \notin \Sigma ^{w+1}(\mathsf {inj}({\mathbf {k}} Q))$. It follows that 
$\Theta$ is surjective.
To see that 
$\Theta$ is injective, suppose 
$\mathsf {S}$ is a simple-minded collection of 
$\mathsf {D}$ contained in 
$\mathcal {F}_{-w}$ such that 
$\Theta (\mathsf {S}) = \mathsf {T}$. Let 
$\mathsf {P} = \mathsf {S} \setminus \mathsf {T}$ and note that 
$\mathsf {P} \subseteq \Sigma ^{w+1} \mathsf {H} \cap (\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp$. It follows, by the hereditary property, that for each 
$P \in \mathsf {P}$ the object 
$T_P$ in the truncation triangle (5) must be zero, whence 
$\Phi (\mathsf {P}) = \mathsf {P}$. In particular, by Proposition 5.5 and Lemma 5.7, 
$\mathsf {P}$ is a simple-minded collection of 
$(\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp$ such that 
$\mathsf {P} \subseteq \Sigma ^{w+1} \mathsf {E}^{\perp _{\mathsf {H}}}$, i.e. is concentrated in one degree with respect to the standard heart 
$\mathsf {E}^{\perp _{\mathsf {H}}} \simeq \mathsf{mod}( {{\mathbf {k}} Q'})$ in 
$(\Sigma ^{\mathbb {Z}} \mathsf {T})^\perp \simeq \mathsf {D}^b({\mathbf {k}} Q')$. Therefore, the objects of 
$\mathsf {P}$ can be ordered into an exceptional sequence by Lemma 5.1. It now follows by [Reference RingelRin94, Theorem 3], which asserts that the unique orthogonal complete exceptional sequence in 
$\mathsf{mod}({{\mathbf {k}} Q'})$ is that consisting of the simple 
${\mathbf {k}} Q'$-modules. Hence, 
$\mathsf {P} = \mathsf {R}$ and 
$\Theta$ is injective.
6. Noncrossing partitions
Let 
$Q$ be an acyclic quiver. In this section, we establish a bijection between 
$w$-simple-minded systems in 
$\mathsf {C}_{-w}({\mathbf {k}} Q)$ and positive 
$w$-noncrossing partitions of the corresponding Weyl group 
$W_Q$. This bijection generalises the existing bijection in the case that 
$Q$ is Dynkin, see [Reference Buan, Reiten and ThomasBRT12, Reference Coelho SimõesCoe12, Reference Iyama and JinIJ20]. The strategy follows that of [Reference Coelho SimõesCoe12]. We start with a brief review of the Weyl group of an acyclic quiver and noncrossing partitions. The main reference for the Weyl group is [Reference RingelRin94], whereas for noncrossing partitions we refer to [Reference ArmstrongArm09].
6.1 Weyl group and noncrossing partitions
Consider the symmetric bilinear form on the Grothendieck group 
$K_0 ({\mathbf {k}} Q)$ defined by
\[ ([X],[Y]) \mathrel{\mathop:}= \dim \mathsf{Hom}_{{\mathbf{k}} Q} (X,Y) + \dim \mathsf{Hom}_{{\mathbf{k}} Q} (Y,X) - \dim \mathsf{Ext}^1_{{\mathbf{k}} Q} (X,Y) - \dim \mathsf{Ext}^1_{{\mathbf{k}} Q} (Y,X), \]
for 
$X, Y \in \mathsf{mod}({{\mathbf {k}} Q})$. Given 
$X \in K_0 ({\mathbf {k}} Q)$ with 
$(X,X) \in \{-2,-1,1,2\}$, the reflection 
$t_X$ along 
$X$ is the isometry
\[ t_X \colon K_0 ({\mathbf{k}} Q) \longrightarrow K_0 ({\mathbf{k}} Q), \quad t_X (Y) = Y - \frac{2 (Y,X)}{(X,X)} X . \]
Let 
$S_1, \ldots, S_n$ be the simple 
${\mathbf {k}} Q$-modules and note that 
$([S_i],[S_i])=2$. The Weyl group 
$W_Q$ associated to the quiver 
$Q$ is the group of isometries generated by 
$R \mathrel {\mathop :}= \{t_{[S_1]}, \ldots, t_{[S_n]}\}$. The set 
$R$ is called the set of simple reflections of 
$W_Q$, and the set of all reflections in 
$W_Q$ is denoted by 
$T$.
The absolute length of 
$w \in W_Q$, denoted by 
$\ell _T (w)$, is the minimum length of 
$w$ written as a product of reflections. We call a minimum length expression for 
$w$ written as a product of reflections a 
$T$-reduced expression of 
$w$; we denote the set of all such expressions by 
$\mathsf {red}_T (w)$.
A parabolic subgroup of 
$W_Q$ is a subgroup of 
$W_Q$ generated by a subset of 
$R$. The following result, which holds for any Coxeter group 
$W$ of finite rank, will be useful later.
Theorem 6.1 [Reference Baumeister, Dyer, Stump and WegenerBDSW14, Theorem 1.4]
Let 
$W'$ be a parabolic subgroup of 
$W$. For each 
$u \in W'$, we have 
$\mathsf {red}_T (u) = \mathsf {red}_{T'} (u)$, where 
$T' = W' \cap T$ is the set of reflections in 
$W'$.
Recall, for example from [Reference Ingalls and ThomasIT09, § 3.1], that a Coxeter element of 
$W_Q$ is the product of all the simple reflections in some order; in [Reference ArmstrongArm09], a Coxeter element is called a standard Coxeter element. From now on, we fix a Coxeter element 
$c \in W_Q$ such that the ordering of the product of simple reflections giving rise to 
$c$ corresponds to an ordering of the simple 
${\mathbf {k}} Q$-modules into an exceptional sequence. Note that 
$\ell _T (c) = n$. We can now define (positive) 
$w$-noncrossing partitions for 
$w \geqslant 1$; see [Reference ArmstrongArm09].
Definition 6.2 Let 
$w \geqslant 1$, 
$\mathbf {u} = (u_1, \ldots, u_{w+1})$ be a 
$(w+1)$-tuple of elements of 
$W_Q$ and 
$c$ be the Coxeter element fixed above. The tuple 
$\mathbf {u}$ is said to be:
(i) a
$w$-noncrossing partition if $c = u_1 u_2 \cdots u_{w+1}$ and $n = \ell _T (c) = \ell _T (u_1) + \cdots + \ell _T (u_{w+1})$; and(ii) a positive
$w$-noncrossing partition if it is a $w$-noncrossing partition such that the product $u_2 \cdots u_{w+1}$ does not lie in any proper parabolic subgroup.
The set of (positive) 
$w$-noncrossing partitions of 
$W_Q$ with respect to 
$c$ is denoted by 
$\mathsf {NC}_w^{(+)} (W_Q)$, with the fixed Coxeter element 
$c$ understood implicitly.
We end this section with the following useful connection between exceptional sequences and expressions for the Coxeter element.
Theorem 6.3 [Reference Igusa and SchifflerIS10, Theorem 4.1]
Let 
$Q$ be an acyclic quiver. Then the following assertions hold.
(1) For any exceptional
${\mathbf {k}} Q$-module $E$, we have $t_{[E]} \in T$.(2) If
$(X_1, \ldots, X_n)$ is a complete exceptional sequence in $\mathsf{mod}({{\mathbf {k}} Q})$, setting $t_i = t_{[X_i]}$, we have $c = t_1 \cdots t_n$.(3) If
$c = t_1 \cdots t_n$, with $t_i \in T$, then $t_i = t_{[X_i]}$, for some exceptional ${\mathbf {k}} Q$-module $X_i$, and $(X_1, \ldots, X_n)$ is a complete exceptional sequence.
It follows from Theorem 6.3 that the set of (positive) noncrossing partitions does not depend on the ordering of the set of simple 
${\mathbf {k}} Q$-modules into an exceptional sequence.
6.2 Simple-minded collections and noncrossing partitions
For an acyclic quiver 
$Q$ and an integer 
$w \geqslant 1$, we recall the construction of a bijective map
\begin{equation} \varphi \colon \mathsf{NC}_w (W_Q) \stackrel{1-1}{\longrightarrow} \Big\{ \begin{matrix} \textrm{simple-minded collections of}\ \mathsf{D}^b({\mathbf{k}}\, Q)\\ \textrm{contained in}\ \mathsf{X} \cap \Sigma^{w+1} \mathsf{Y}\end{matrix} \Big\} \end{equation}
from [Reference Buan, Reiten and ThomasBRT12, Theorem 7.3]; see [Reference Coelho SimõesCoe12] for a similarly constructed map in the case that 
$Q$ is Dynkin. Let 
$\mathbf {u} = (u_1, \ldots, u_{w+1}) \in \mathsf {NC}_w (W_Q)$. We construct 
$\varphi (\mathbf {u})$ in two steps.
• We have
$c = u_1 \cdots u_{w+1}$ and $n = \ell _T (u_1) + \ell _T (u_2) + \cdots + \ell _T (u_{w+1})$. For each $1 \leqslant i \leqslant w+1$, pick a $T$-reduced expression for $u_i$. The ordered product of these expressions gives rise to a $T$-reduced expression for $c$ and by Theorem 6.3(3) we obtain a complete exceptional sequence $\mathsf {E} = (\mathsf {E}_1,\ldots,\mathsf {E}_{w+1})$ in $\mathsf{mod}({{\mathbf {k}} Q})$, where $\mathsf {E}_i$ is the subsequence of $\mathsf {E}$ corresponding to the $T$-reduced expression of $u_i$.• Let
$\mathcal {C}_i$ be the smallest wide (i.e. exact abelian extension-closed) subcategory of $\mathsf{mod}({{\mathbf {k}} Q})$ containing $\mathsf {E}_i$. By [Reference Crawley-BoeveyCra93, Lemma 5], $\mathcal {C}_i$ is equivalent to $\mathsf{mod}( {{\mathbf {k}} Q_i})$ for some acyclic quiver $Q_i$ with $\ell _T(u_i)$ vertices. Let $\mathsf {S}_i$ be the set of simples in $\mathcal {C}_i$. Then we define
The fact that\[ \varphi (\mathbf{u}) \mathrel{\mathop:}= \bigcup_{i = 1}^{w+1} \Sigma^{w+1-i} \mathsf{S}_i. \]$\varphi (\mathbf {u})$ is independent of the choice of $T$-reduced expression follows from [Reference Igusa and SchifflerIS10, Theorem 4.3].
We now come to the main theorem of this section. The case when 
$Q$ is Dynkin and 
$w=1$ was given in [Reference Coelho SimõesCoe12, Theorem 5.7]. The case when 
$Q$ is Dynkin and 
$w \geqslant 1$ is an integer was established in [Reference Buan, Reiten and ThomasBRT12, Theorem 7.4] (see also [Reference Iyama and JinIJ20, Theorem 1.1]), via bijections with 
$m$-clusters, and using a different description of positive 
$w$-noncrossing partitions. Before proceeding, we require a definition.
For a 
${\mathbf {k}} Q$-module 
$X$, the support of 
$X$ is 
$\mathsf {supp}(X) \mathrel {\mathop :}= \{a \in Q_0 \mid \mathsf {Hom} (P_a, X) \neq 0 \}$. Equivalently, 
$\mathsf {supp}(X) = \{a \in Q_0 \mid S_a \text { occurs in a composition series for } X\}$. For a set 
$\mathsf {X}$ of 
${\mathbf {k}} Q$-modules the support of 
$\mathsf {X}$ is 
$\mathsf {supp}(\mathsf {X}) = \bigcup _{X \in \mathsf {X}} \mathsf {supp}(X)$.
Theorem 6.4 Let 
$Q$ be an acyclic quiver. The map 
$\varphi$ defined in (7) restricts to a bijection
\[ \varphi \colon \mathsf{NC}_w^+ (W_Q) \stackrel{1-1}{\longrightarrow} \Big\{ \begin{matrix} \textrm{simple-minded collections of}\ \mathsf{D}^b({\mathbf{k}}\, Q)\\ \textrm{contained in}\ \mathcal{F}_{{-}w}\end{matrix} \Big\}. \]Proof. Let 
$\mathbf {u} = (u_1, u_2, \ldots, u_{w+1}) \in \mathsf {NC}_w^+ (W_Q)$. Then, by the construction of the map 
$\varphi$ in (7), 
$\varphi (\mathbf {u}) = \bigcup _{i = 1}^{w+1} \Sigma ^{w+1-i} \mathsf {S}_i$ is a simple-minded collection of 
$\mathsf {D}^b({\mathbf {k}} Q)$ lying in 
$\mathsf {X} \cap \Sigma ^{w+1} \mathsf {Y}$. To see that the restriction is well defined, by Theorem 5.8, it suffices to check that 
$\bigcup _{i = 2}^{w+1} \Sigma ^{w+1-i} \mathsf {S}_i \subseteq \mathsf {X} \cap \Sigma ^w \mathsf {Y}$ is an exceptionally finite, 
$w$-sincere 
$\infty$-orthogonal collection in 
$\mathsf {D}^b({\mathbf {k}} Q)$. This set is clearly 
$\infty$-orthogonal. Functorial finiteness and exceptionality follow immediately from Lemma 3.3(3) and Corollary 3.7, and Lemma 5.1, respectively. Only 
$w$-sincerity remains to be checked.
Suppose for a contradiction that 
$\bigcup _{i = 2}^{w+1} \Sigma ^{w+1-i} \mathsf {S}_i \subseteq \mathsf {X} \cap \Sigma ^w \mathsf {Y}$ is not 
$w$-sincere. We claim that if 
$E$ is an exceptional 
${\mathbf {k}} Q$-module, then 
$t_{[E]}$ lies in the parabolic subgroup generated by 
$\{t_{[S_a]} \in R \mid a \in \mathsf {supp}(E) \}$. Indeed, consider the wide subcategory 
$\mathcal {C}_E$ generated by the set of simple 
${\mathbf {k}} Q$-modules 
$\{S_a \mid a \in \mathsf {supp}(E) \}$. The exceptional module 
$E$ lies in 
$\mathcal {C}_E$ and it can be extended to a complete exceptional sequence 
$\mathsf {E}$ in 
$\mathcal {C}_E$ (see [Reference Crawley-BoeveyCra93, Lemma 1]). By the transitivity of the action of the braid group on the set of complete exceptional sequences (see [Reference Crawley-BoeveyCra93] again), 
$\mathsf {E}$ is obtained from the set 
$\{S_a \mid a \in \mathsf {supp}(\mathsf {E}) \}$ ordered into a complete exceptional sequence in 
$\mathcal {C}_E$, via a sequence of mutations corresponding to the braid group action. The claim then follows from [Reference Igusa and SchifflerIS10, § 2.2]. As a consequence, we have that 
$u_2 \cdots u_{w+1}$ lies in the parabolic subgroup generated by 
$\{t_{[S_a]} \in R \mid a \in \mathsf {supp}(\bigcup _{i = 2}^{w+1} \mathsf {E}_i) \}$. This subgroup is a proper parabolic subgroup because 
$\bigcup _{i = 2}^{w+1} \mathsf {E}_i$ is not sincere, as 
$\mathsf {supp}(\mathsf {S}_i) = \mathsf {supp}(\mathcal {C}_i) = \mathsf {supp}(\mathsf {E}_i)$, for each 
$i$. This contradicts the fact that 
$\mathbf {u}$ is a positive 
$w$-noncrossing partition. Therefore, 
$\bigcup _{i = 2}^{w+1} \Sigma ^{w+1-i} \mathsf {S}_i \subseteq \mathsf {X} \cap \Sigma ^w \mathsf {Y}$ is indeed 
$w$-sincere.
As 
$\varphi$ is the restriction of a bijection, it is clearly injective. It remains to check that 
$\varphi$ is surjective. Let 
$\mathsf {S}$ be a simple-minded collection contained in 
$\mathcal {F}_{-w}$. By Lemma 5.1, we can order the elements in 
$\mathsf {S}$ into a (complete) exceptional sequence 
$\mathsf {E}$ in which the cohomological degrees are weakly decreasing. For each 
$1\leqslant i \leqslant w+1$, let 
$\mathsf {E}_i$ the subsequence consisting of the elements of cohomological degree 
$i-1$, and 
$\mathcal {C}_i$ be the smallest wide subcategory of 
$\mathsf{mod}({{\mathbf {k}} Q})$ containing 
$H(\mathsf {E}_i)$, where 
$H \colon \mathsf {D}^b({\mathbf {k}} Q) \to \mathsf{mod}({{\mathbf {k}} Q})$ is the standard cohomology functor; see (4). Order the simple objects of 
$\mathcal {C}_i$ into an exceptional sequence (cf. [Reference RingelRin94, Theorem 3]), and let 
$u_i$ be the product of the corresponding reflections respecting the order of the exceptional sequence, which gives a 
$T$-reduced expression for 
$u_i$. Then 
$\mathbf {u} = (u_{w+1}, \ldots, u_1)$ is a 
$w$-noncrossing partition and 
$\varphi (\mathbf {u}) = \mathsf {S}$.
Finally, we must check that 
$\mathbf {u}$ is positive. Suppose 
$\mathbf {u}$ is not positive. Then 
$u_w \cdots u_1$ lies in a proper parabolic subgroup 
$W_J$ generated by 
$J \subsetneq R$. For each 
$1 \leqslant i \leqslant w$, each reflection appearing in the 
$T$-reduced expression of 
$u_i$ above lies in 
$W_J$ by Theorem 6.1. This means that for 
$1 \leqslant i \leqslant w$ the simple objects of 
$\mathcal {C}_i$ do not have support at the vertices of 
$Q$ corresponding to the simple reflections at 
$R \setminus J$. As the support of 
$H(\mathsf {E}_i)$ coincides with that of the simple objects in 
$\mathcal {C}_i$, it follows that 
$\mathsf {S} \cap \mathsf {X} \cap \Sigma ^w \mathsf {Y}$ is not 
$w$-sincere, contradicting Theorem 5.8. Hence, 
$\mathbf {u}$ must be positive and 
$\varphi$ is surjective.
Acknowledgements
We would like to thank Lidia Angeleri Hügel, Jorge Vitória and Alexandra Zvonareva for useful discussions. We particularly thank Alexandra Zvonareva for kindly allowing us to add her joint work with the first two authors as an appendix. The authors are grateful to Peter Jørgensen and Haruhisa Enomoto for pointing out a gap in our original proof of Theorem C, and an anonymous referee for useful comments and suggestions. The first author is grateful to the European Union's Horizon 2020 research and innovation programme for financial support through the Marie Skłodowska-Curie Individual Fellowship grant agreement number 838706.
Appendix A. Reduction of simple-minded collections revisited
Raquel Coelho Simões, David Pauksztello and Alexandra Zvonareva
In this appendix, we provide an alternative proof of [Reference JinJin19, Theorem 3.1], which avoids using a Verdier localisation and is similar to the analogous result for simple-minded systems in [Reference Coelho Simões and PauksztelloCP20, Section 6].
Throughout, 
$\mathsf {D}$ is a Hom-finite, Krull–Schmidt, 
${\mathbf {k}}$-linear triangulated category with shift functor 
$\Sigma \colon \mathsf {D} \to \mathsf {D}$. We impose the following setup.
Setup A.1 Let 
$\mathsf {S}$ be an 
$\infty$-orthogonal collection of objects in 
$\mathsf {D}$ and 
$\mathsf {Z}$ a subcategory of 
$\mathsf {D}$ satisfying the following conditions:
(1)
$\langle \mathsf {S} \rangle$ is covariantly finite in ${}^\perp (\Sigma ^{< 0} \mathsf {S})$ and contravariantly finite in $(\Sigma ^{> 0} \mathsf {S})^\perp$;(2) for
$d \in \mathsf {D}$, we have $\mathsf {Hom}_\mathsf {D} (d, \Sigma ^{\ll 0} \mathsf {S}) = 0$ and $\mathsf {Hom}_\mathsf {D} (\Sigma ^{\gg 0} \mathsf {S}, d) = 0$; and(3)
$\mathsf {Z} \mathrel {\mathop :}= {}^\perp (\Sigma ^{\leqslant 0} \mathsf {S}) \cap (\Sigma ^{\geqslant 0} \mathsf {S})^\perp$.
In fact, if 
$\mathsf {D} = \mathsf {D}^b(A)$ for a finite-dimensional algebra 
$A$, the stronger condition that 
$\langle \mathsf {S} \rangle$ is functorially finite in 
$\mathsf {D}^b(A)$ holds by Lemmas 3.3(3) and 3.7.
We recall the following construction from [Reference Coelho Simões and PauksztelloCP20, Section 4] (see also [Reference JinJin19, Reference NakaokaNak18]).
• For an object
$z \in \mathsf {Z}$, a functor $\langle 1 \rangle \colon \mathsf {Z} \to \mathsf {Z}$ is defined on objects by taking the cone of a minimal right $\langle \mathsf {S} \rangle$-approximation: $s_z\rightarrow \Sigma z\rightarrow z\langle 1 \rangle \rightarrow \Sigma s_z$. The functor $\langle 1 \rangle$ is defined on morphisms in the obvious way, and its quasi-inverse $\langle -1 \rangle$ by the dual construction; see [Reference Coelho Simões and PauksztelloCP20, Lemma 3.6].• For a morphism
$f \colon x \to y$ in $\mathsf {Z}$, consider the triangle $x\stackrel {f}{\longrightarrow } y\stackrel {g_1}{\longrightarrow } c_f\stackrel {h_1}{\longrightarrow } \Sigma x$ in $\mathsf {D}$ together with the minimal right $\langle \mathsf {S} \rangle$-approximation triangles of $c_f$ and $\Sigma x$ and complete to the following commutative diagram.
Note that applying$\mathsf {Hom}_\mathsf {D}(\Sigma ^{>0} \mathsf {S},-)$ to the triangle $x\rightarrow y\rightarrow c_f\rightarrow \Sigma x$ shows that both $c_f, \Sigma x \in (\Sigma ^{>0} \mathsf {S})^\perp$ so that the required approximations exist.
Theorem A.2 [Reference JinJin19, Proposition 3.6]
The category 
$(\mathsf {Z},\langle 1 \rangle )$ admits a triangulated structure with standard triangles given by diagrams of the form 
$x \stackrel {f}{\longrightarrow } y \longrightarrow z_f \longrightarrow x\langle 1 \rangle$.
Proof. This can be proved in several ways. On one hand, observe that 
$\mathsf {S}$ and 
$\mathsf {Z}$ given in Setup A.1 satisfy [Reference Coelho Simões and PauksztelloCP20, Lemma 6.3] so that [Reference Coelho Simões and PauksztelloCP20, Theorem 4.1] can be applied. Otherwise, one can proceed via Jin's construction in [Reference JinJin19, Proposition 3.6], or Nakaoka's construction in [Reference NakaokaNak18, Theorem 4.15].
Because there are two triangulated structures under consideration, we differentiate them as in [Reference Coelho Simões and PauksztelloCP20, Section 6] with the following notation. Let 
$\mathsf {X}$ and 
$\mathsf {Y}$ be subcategories of 
$\mathsf {Z}$. We define
\[ \mathsf{X} \star \mathsf{Y} \mathrel{\mathop:}= \{ z \in \mathsf{Z} \mid \text{there exists a triangle } x \to z \to y \to x\langle 1 \rangle \text{ with } x \in \mathsf{X} \text{ and } y \in \mathsf{Y}\}. \]
We denote the extension closure of 
$\mathsf {X}$ with respect to the triangulated structure in 
$\mathsf {Z}$ by 
$\{ \mathsf {X} \}$. The notation 
$\mathsf {X} * \mathsf {Y}$ and 
$\langle \mathsf {X} \rangle$ keep their usual meanings in 
$\mathsf {D}$.
Before giving our alternative proof of [Reference JinJin19, Theorem 3.1], we collect some preliminary statements.
Lemma A.3 Let 
$\mathsf {S}$ and 
$\mathsf {Z}$ be as in Setup A.1. Suppose one of the two conditions holds:
(a)
$\mathsf {S} \subseteq \mathsf {T}$ and $\mathsf {T}$ is a simple-minded collection in $\mathsf {D}$; in which case set $\mathsf {R} = \mathsf {T} \setminus \mathsf {S}$; or(b)
$\mathsf {T} = \mathsf {S} \cup \mathsf {R}$, where $\mathsf {R}$ is a simple-minded collection in $\mathsf {Z}$.
Then the following hold:
(1) for
$i \geqslant j$, $\{\mathsf {R}\langle i \rangle \} \star \{\mathsf {R}\langle i-1 \rangle \} \star \cdots \star \{\mathsf {R}\langle j \rangle \} \subseteq \langle \Sigma ^i \mathsf {T} \rangle * \langle \Sigma ^{i-1} \mathsf {T} \rangle * \cdots * \langle \Sigma ^j \mathsf {T} \rangle$;(2)
$\mathsf {susp}_\mathsf {D}\ \mathsf {T} \cap \mathsf {Z} = \mathsf {susp}_\mathsf {Z}\ \mathsf {R}$;(3)
$\mathsf {cosusp}_\mathsf {D}\ \mathsf {T} \cap \mathsf {Z} = \mathsf {cosusp}_\mathsf {Z}\ \mathsf {R}$;(4)
$\mathsf {susp}_{\mathsf {D}}\ \mathsf {S}$ is contravariantly finite in $\mathsf {D}$;(5)
$\mathsf {cosusp}_{\mathsf {D}}\ \mathsf {S}$ is covariantly finite in $\mathsf {D}$.
Proof. Statement (1) can be argued as in Claims A and B in the proof of [Reference Coelho Simões and PauksztelloCP20, Theorem 6.6]; see also [Reference JinJin19, Lemma 3.4]. Statements (2) and (3) can be argued using [Reference Coelho Simões and PauksztelloCP20, Lemma 6.5] as the start of an induction. Statements (4) and (5) follow immediately from conditions 
$(1)$ and 
$(2)$ in Setup A.1 using a standard argument; cf. the proof of Proposition 4.2.
Theorem A.4 [Reference JinJin19, Theorem 3.1]
Let 
$\mathsf {S}$ and 
$\mathsf {Z}$ be as in Setup A.1. Then there is a bijection
\begin{align*} \{ \text{simple-minded collections in}\ \mathsf{D}\ \text{containing}\ \mathsf{S}\} & \stackrel{1-1}{\longleftrightarrow} \{ \text{simple-minded collections in}\ \mathsf{Z} \}. \\ \mathsf{T} & \longmapsto \mathsf{T} \setminus \mathsf{S} \end{align*}Proof. Let 
$\mathsf {T}$ be a simple-minded collection in 
$\mathsf {D}$ containing 
$\mathsf {S}$. We want to show that 
$\mathsf {R} \mathrel {\mathop :}= \mathsf {T} \setminus \mathsf {S}$ is a simple-minded collection in 
$\mathsf {Z}$. We use the characterisation of simple-minded collections in Proposition 3.6.
First, observe that 
$\mathsf {R}$ is an 
$\infty$-orthogonal collection in 
$\mathsf {Z}$, for instance, by using the dimension shifting argument in the proof of [Reference Coelho Simões and PauksztelloCP20, Theorem 6.6].
The next step is to show that 
${}^\perp (\mathsf {R} \langle < 0 \rangle ) \cap (\mathsf {R} \langle \geqslant 0 \rangle )^\perp = 0$. Suppose 
$z \in \mathsf {Z}$ is such that 
$z \in {}^\perp (\mathsf {R} \langle < 0 \rangle ) \cap (\mathsf {R} \langle \geqslant 0 \rangle )^\perp$. As 
$\mathsf {Hom}_\mathsf {D} (z \langle >0 \rangle, \mathsf {R}) \simeq \mathsf {Hom}_\mathsf {D} (\Sigma ^{>0} z, \mathsf {R})$ and 
$\mathsf {Hom}_\mathsf {D} (\mathsf {R}, z \langle \leqslant 0 \rangle ) \simeq \mathsf {Hom}_\mathsf {D} (\mathsf {R}, \Sigma ^{\leqslant 0} z)$ by the dimension-shifting argument above, it follows that 
$z \in {}^\perp (\Sigma ^{<0} \mathsf {R}) \cap (\Sigma ^{\geqslant 0} \mathsf {R})^\perp$. As 
$z \in \mathsf {Z}$, it follows that 
$z \in {}^\perp (\Sigma ^{<0} \mathsf {T}) \cap (\Sigma ^{\geqslant 0} \mathsf {T})^\perp$, and so 
$z = 0$, as 
$\mathsf {T}$ is 
$\infty$-Riedtmann in 
$\mathsf {D}$ by Proposition 3.6.
Finally, we show that 
$\mathsf {cosusp}_\mathsf {Z}\ \mathsf {R}$ is covariantly finite in 
$\mathsf {Z}$. By Lemma A.3(1), we have 
$\mathsf {cosusp}_\mathsf {Z}\ \mathsf {R} \subseteq \mathsf {cosusp}_\mathsf {D}\ \mathsf {T}$. By Lemma A.3(3), we have 
$(\mathsf {cosusp}_\mathsf {D}\ \mathsf {T} )\cap \mathsf {Z} = \mathsf {cosusp}_\mathsf {Z}\ \mathsf {R}$. As 
$\mathsf {T}$ is a simple-minded collection in 
$\mathsf {D}$, 
$\mathsf {cosusp}_\mathsf {D}\ \mathsf {T}$ is covariantly finite in 
$\mathsf {D}$. Therefore, for 
$z \in \mathsf {Z} \subseteq \mathsf {D}$, we can take a decomposition triangle, 
$x\stackrel {f}{\longrightarrow } z\longrightarrow t_z\longrightarrow \Sigma x$, in 
$\mathsf {D}$ with 
$x \in {}^\perp (\mathsf {cosusp}_\mathsf {D}\ \mathsf {T}) \subseteq {}^\perp (\Sigma ^{\leqslant 0} \mathsf {S})$. An inspection of the resulting long exact sequence shows that 
$x \in (\Sigma ^{\geqslant 0} \mathsf {S})^\perp$, and hence 
$x \in \mathsf {Z}$. Now taking the cone of a minimal right 
$\langle \mathsf {S} \rangle$-approximation 
$s_f \longrightarrow t_z$ of 
$t_z$ gives a triangle in 
$\mathsf {Z}$:
\[ x \stackrel{f}{\longrightarrow} z \longrightarrow z_f \longrightarrow x\langle 1 \rangle. \]
We claim that the third term 
$z_f$ lies in 
$(\mathsf {cosusp}_\mathsf {D}\ \mathsf {T}) \cap \mathsf {Z}$ and, hence, in 
$\mathsf {cosusp}_\mathsf {Z}\ \mathsf {R}$, which makes the triangle above into a decomposition triangle for 
$z$ in 
$\mathsf {Z}$ because 
$x \in {}^\perp (\mathsf {cosusp}_\mathsf {D}\ \mathsf {T}) \subseteq {}^\perp (\mathsf {cosusp}_\mathsf {Z}\ \mathsf {R})$. In particular, showing that 
$\mathsf {cosusp}_\mathsf {Z}\ \mathsf {R}$ is covariantly finite in 
$\mathsf {Z}$. The argument for the contravariant finiteness of 
$\mathsf {susp}_\mathsf {Z}\ \mathsf {R}$ in 
$\mathsf {Z}$ is similar. Now applying Proposition 3.6, we conclude that 
$\mathsf {R}$ is a simple-minded collection in 
$\mathsf {Z}$.
Therefore, we need to establish the claim above. As 
$t_z \in \mathsf {cosusp}_\mathsf {D}\ \mathsf {T}$, there is a triangle 
$t'\rightarrow t_z\rightarrow t''\rightarrow \Sigma t'$ with 
$t' \in \langle \mathsf {T} \rangle$ and 
$t'' \in \mathsf {cosusp}_\mathsf {D}\ \Sigma ^{-1} \mathsf {T}$. Combining this triangle with that coming from the minimal right 
$\langle \mathsf {S} \rangle$-approximation gives the following commutative diagram by the octahedral axiom.
Examining the long exact sequence obtained by applying 
$\mathsf {Hom}_\mathsf {D}(\mathsf {S},-)$ to the lower horizontal triangle shows that 
$g \colon s_f \to t'$ is a right 
$\langle \mathsf {S} \rangle$-approximation. If it were not minimal, then 
$s_f \to t_z$ would also fail to be minimal. Therefore, 
$g \colon s_f \to t'$ is a minimal right 
$\langle \mathsf {S} \rangle$-approximation and 
$t_1 \in \langle \mathsf {T} \rangle$ by [Reference Coelho Simões and PauksztelloCP20, Theorem 2.11]. Hence, 
$z_f \in \mathsf {cosusp}_\mathsf {D}\ \mathsf {T}$, as required.
Conversely, suppose 
$\mathsf {R}$ is a simple-minded collection in 
$\mathsf {Z}$. We show that 
$\mathsf {T} \mathrel {\mathop :}= \mathsf {S} \cup \mathsf {R}$ is a simple-minded collection in 
$\mathsf {D}$. The proof that 
$\mathsf {T}$ is an 
$\infty$-orthogonal collection is similar to the corresponding argument above in the other direction.
Let 
$d$ be an object in 
$\mathsf {D}$. By Lemma A.3(4) and (5), we have that 
$\mathsf {susp}_\mathsf {D}\ \mathsf {S}$ is contravariantly finite in 
$\mathsf {D}$ and 
$\mathsf {cosusp}_\mathsf {D}\ \mathsf {S}$ is covariantly finite in 
$\mathsf {D}$. Decomposing first with respect to the t-structure 
$(\mathsf {susp}_\mathsf {D}\ \mathsf {S}, (\Sigma ^{\geqslant 0} \mathsf {S})^\perp )$ and then the t-structure 
$({}^\perp (\Sigma ^{\leqslant 0} \mathsf {S}), \mathsf {cosusp}_\mathsf {D}\ \mathsf {S})$ gives the following triangles,
\[ x\rightarrow d\rightarrow y\rightarrow \Sigma x \quad \text{and} \quad z\rightarrow y\rightarrow v\rightarrow \Sigma z, \]
in which 
$z \in \mathsf {Z} = {}^\perp (\Sigma ^{\leqslant 0} \mathsf {S}) \cap (\Sigma ^{\geqslant 0} \mathsf {S})^\perp$, 
$v \in \mathsf {cosusp}_\mathsf {D}\ \mathsf {S}$ and 
$x \in \mathsf {susp}_\mathsf {D}\ \mathsf {S}$. This shows that 
$\mathsf {D} = (\mathsf {susp}_\mathsf {D}\ \mathsf {S}) * \mathsf {Z} * (\mathsf {cosusp}_\mathsf {D}\ \mathsf {S})$, cf. [Reference JinJin19, Proposition 3.3]. Now, Lemma A.3(1), shows that 
$\mathsf {Z} = \mathsf {thick}_{\mathsf {Z}}(\mathsf {R}) \subseteq \mathsf {thick}_{\mathsf {D}}(\mathsf {T})$, from which it follows that 
$\mathsf {D} = \mathsf {thick}_{\mathsf {D}}(\mathsf {T})$, and we conclude that 
$\mathsf {T}$ is a simple-minded collection.
Open access
