Published online by Cambridge University Press: 03 November 2022
We establish central limit theorems for an action of a group 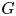 $G$ on a hyperbolic space
$G$ on a hyperbolic space 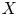 $X$ with respect to the counting measure on a Cayley graph of
$X$ with respect to the counting measure on a Cayley graph of 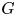 $G$. Our techniques allow us to remove the usual assumptions of properness and smoothness of the space, or cocompactness of the action. We provide several applications which require our general framework, including to lengths of geodesics in geometrically finite manifolds and to intersection numbers with submanifolds.
$G$. Our techniques allow us to remove the usual assumptions of properness and smoothness of the space, or cocompactness of the action. We provide several applications which require our general framework, including to lengths of geodesics in geometrically finite manifolds and to intersection numbers with submanifolds.
Gekhtman is partially supported by NSERC. Taylor is partially supported by NSF grants DMS-1744551, DMS-2102018 and the Sloan Foundation. Tiozzo is partially supported by NSERC, an Ontario Early Researcher Award and the Sloan Foundation.