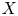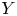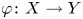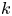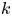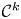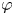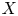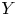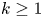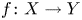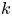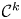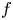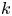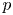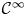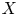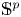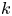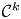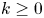1. Introduction
Regulous geometry has recently emerged as a subfield of real algebraic geometry. It deals with rational maps that admit continuous extensions or extensions satisfying certain differentiability conditions. In the following, we develop new methods that lead to a much better understanding of the relationship between the concepts of approximation and homotopy of maps in the framework of regulous geometry.
Throughout this paper we use the term real algebraic variety to mean a ringed space with the structure sheaf of 
$\mathbb {R}$-algebras of 
$\mathbb {R}$-valued functions, which is isomorphic to a Zariski locally closed subset of real projective 
$n$-space 
$\mathbb {P}^n(\mathbb {R})$, for some 
$n$, endowed with the Zariski topology and the sheaf of regular functions. This is compatible with [Reference Bochnak, Coste and RoyBCR98, Reference MangolteMan20], which contain a detailed exposition of real algebraic geometry. Recall that each real algebraic variety in the sense used here is actually affine, that is, isomorphic to an algebraic subset of 
$\mathbb {R}^n$ for some 
$n$ (see [Reference Bochnak, Coste and RoyBCR98, Proposition 3.2.10 and Theorem 3.4.4]). Morphisms of real algebraic varieties are called regular maps. Each real algebraic variety carries also the Euclidean topology determined by the usual metric on 
$\mathbb {R}$. Unless explicitly stated otherwise, all topological notions relating to real algebraic varieties refer to the Euclidean topology.
As a matter of convention, all 
$\mathcal {C}^{\infty }$ manifolds will be Hausdorff and second countable. The space 
$\mathcal {C}^k(M,N)$ of 
$\mathcal {C}^k$ maps between 
$\mathcal {C}^{\infty }$ manifolds, where 
$k$ is a nonnegative integer or 
$k=\infty$, is endowed with the 
$\mathcal {C}^k$ topology (see [Reference HirschHir97, pp. 34, 36] or [Reference WallWal16, p. 311] for the definition of this topology and note that in [Reference HirschHir97] it is called the weak 
$\mathcal {C}^k$ topology; the 
$\mathcal {C}^0$ topology is just the compact-open topology).
Let 
$X$, 
$Y$ be two nonsingular real algebraic varieties. A map 
$f \colon X \to Y$ is said to be regulous if it is continuous on 
$X$ and there exists a Zariski open dense subset 
$U$ of 
$X$ such that the restriction 
$f|_U \colon U \to Y$ is a regular map. Let 
$X(f)$ denote the union of all such 
$U$. The complement 
$P(f) := X \setminus X(f)$ of 
$X(f)$ is the smallest Zariski closed subset of 
$X$ for which the restriction 
$f|_{X \setminus P(f)} \colon X \setminus P(f) \to Y$ is a regular map. If 
$f(P(f)) \neq Y$, we say that 
$f$ is a nice regulous map. In the literature regulous maps are also called continuous rational maps [Reference Kollár, Kucharz and KurdykaKKK18, Reference Kollár and NowakKN15, Reference KucharzKuc09, Reference KucharzKuc13, Reference KucharzKuc14a, Reference KucharzKuc14b, Reference KucharzKuc16a, Reference Kucharz and KurdykaKK16, Reference Kucharz and KurdykaKK17] or stratified-regular maps [Reference KucharzKuc15, Reference Kucharz and KurdykaKK18a, Reference ZielińskiZie16]. The concise name ‘regulous’ was coined by Fichou, Huisman, Mangolte and Monnier [Reference Fichou, Huisman, Mangolte and MonnierFHMM16]. Since the publication of [Reference KucharzKuc09] in 2009 several mathematicians have devoted their attention to regulous maps (see [Reference Bilski, Kucharz, Valette and ValetteBKVV13, Reference CzarneckiCza19, Reference Fernando, Fichou, Quarez and UenoFFQU18, Reference Fichou, Huisman, Mangolte and MonnierFHMM16, Reference Fichou, Monnier and QuarezFMQ17, Reference Fichou, Monnier and QuarezFMQ20, Reference Fichou, Monnier and QuarezFMQ21b, Reference Fichou, Monnier and QuarezFMQ21a, Reference Kollár, Kucharz and KurdykaKKK18, Reference Kollár and NowakKN15, Reference KucharzKuc09, Reference KucharzKuc13, Reference KucharzKuc14a, Reference KucharzKuc14b, Reference KucharzKuc15, Reference KucharzKuc16a, Reference KucharzKuc16b, Reference KucharzKuc20, Reference Kucharz and KurdykaKK16, Reference Kucharz and KurdykaKK17, Reference Kucharz and ZielińskiKZ18, Reference Kucharz and KurdykaKK18a, Reference Kucharz and KurdykaKK18b, Reference MonnierMon18, Reference ZielińskiZie16, Reference ZielińskiZie18] and the references therein).
A map 
$f \colon X \to Y$ is said to be 
$k$-regulous, where 
$k$ is a nonnegative integer or 
$k = \infty$, if it is both regulous and of class 
$\mathcal {C}^k$. Thus, less formally, a 
$k$-regulous map is a 
$\mathcal {C}^k$ map that admits a rational representation. Obviously, ‘
$0$-regulous’ is the same as ‘regulous’. As observed in [Reference KucharzKuc09, Proposition 2.1], 
$\infty$-regulous maps coincide with regular maps, and these are usually studied separately. A standard example of a 
$k$-regulous function, with 
$k$ a nonnegative integer, is 
$f \colon \mathbb {R}^2 \to \mathbb {R}$ defined by
\[
f(x,y) = \frac{x^{3+k}}{x^2+y^2} \quad \text{for } (x,y) \neq (0,0)\quad \text{and}\quad f(0,0)=0.
\]
Clearly, 
$f$ is not of class 
$\mathcal {C}^{k+1}$.
We say that a 
$\mathcal {C}^l$ map 
$f \colon X \to Y$ can be approximated by 
$k$-regulous maps in the 
$\mathcal {C}^k$ topology, where 
$0 \leq k \leq l \leq \infty$, if for every neighborhood 
$\mathcal {U}$ of 
$f$ in 
$\mathcal {C}^k(X,Y)$ there exists a 
$k$-regulous map that belongs to 
$\mathcal {U}$. Investigating whether or not the map 
$f$ admits approximation by 
$k$-regulous maps in the 
$\mathcal {C}^k$ topology, we may assume without loss of generality that 
$f$ is of class 
$\mathcal {C}^{\infty }$. This is justified since the set 
$\mathcal {C}^{\infty }(X,Y)$ is dense in the space 
$\mathcal {C}^k(X,Y)$.
Definition 1.1 An 
$n$-dimensional real algebraic variety 
$Y$ is said to be uniformly rational if every point in 
$Y$ has a Zariski open neighborhood that is biregularly isomorphic to a Zariski open subset of 
$\mathbb {R}^n$.
Clearly, every uniformly rational real algebraic variety is nonsingular of pure dimension. An intriguing open question posed by Gromov is whether every rational nonsingular variety is uniformly rational (see [Reference GromovGro89, p. 885] and [Reference Bogomolov and BöhningBB14] for the discussion involving complex varieties).
One of our main results is the following theorem.
Theorem 1.2 Let 
$k$ be a positive integer, 
$X$ a nonsingular real algebraic variety, and 
$Y$ a uniformly rational real algebraic variety. Then, for a 
$\mathcal {C}^{\infty }$ map 
${f \colon X \to Y}$, the following conditions are equivalent.
(a)
$f$ can be approximated by $k$-regulous maps in the $\mathcal {C}^k$ topology.(b)
$f$ is homotopic to a $k$-regulous map.
It is an open question whether Theorem 1.2 holds for 
$k=0$ or 
$k=\infty$. We also have a more general result, Theorem 4.2, in which the target variety 
$Y$ need not be rational.
The following example illustrates the scope of applicability of Theorem 1.2.
Example 1.3 Here are some uniformly rational real algebraic varieties.
(i) For any nonnegative integer
$n$, the unit $n$-sphere
is uniformly rational because\[ \mathbb{S}^n := \{ (x_0,\ldots,x_n) \in \mathbb{R}^{n+1} : x_0^2 + \cdots+ x_n^2 = 1 \} \]
$\mathbb {S}^n$ with one point removed is biregularly isomorphic to $\mathbb {R}^n$.(ii) Let
$\mathbb {F}$ stand for $\mathbb {R}$, $\mathbb {C}$ or $\mathbb {H}$, where $\mathbb {H}$ is the (skew) field of quaternions. The Grassmannian $\mathbb {G}_d(\mathbb {F}^n)$ of $d$-dimensional $\mathbb {F}$-vector subspaces of $\mathbb {F}^n$ can be regarded as a real algebraic variety (see [Reference Bochnak, Coste and RoyBCR98, pp. 72, 73, 352]) and as such is uniformly rational.(iii) Rational nonsingular real algebraic surfaces are uniformly rational. As detailed in [Reference MangolteMan17, § 2.2], this follows from Comessatti's theorem [Reference ComessattiCom14, p. 257], whose modern proofs are given in [Reference KollárKol01, Theorem 30] and [Reference SilholSil89, p. 137, Proposition 6.4].
(iv) Blow-ups with nonsingular centers of uniformly rational varieties remain uniformly rational, and the proof given in [Reference GromovGro89, p. 885] and [Reference Bogomolov and BöhningBB14] in a complex setting also works for real algebraic varieties.
All previous results on approximation by 
$k$-regulous maps concern maps with values in Grassmann varieties [Reference KucharzKuc09, Reference Kucharz and ZielińskiKZ18, Reference Kucharz and KurdykaKK18a, Reference ZielińskiZie16] or unit spheres [Reference Bilski, Kucharz, Valette and ValetteBKVV13, Reference KucharzKuc09, Reference KucharzKuc13, Reference KucharzKuc14a, Reference KucharzKuc16a, Reference KucharzKuc20, Reference Kucharz and KurdykaKK16, Reference Kucharz and KurdykaKK18a, Reference Kucharz and KurdykaKK18b, Reference ZielińskiZie18]. Theorem 1.2 does not provide any new information in the former case (at least for 
$X$ compact), but opens up new possibilities in the latter.
In view of Theorem 1.2 and Example 1.3(i), we get immediately the following result on maps into 
$\mathbb {S}^p$.
Corollary 1.4 Let 
$k$ be a positive integer, 
$X$ a nonsingular real algebraic variety, and 
$p$ a nonnegative integer. Then, for a 
$\mathcal {C}^{\infty }$ map 
$f \colon X \to \mathbb {S}^p$, the following conditions are equivalent.
(a)
$f$ can be approximated by $k$-regulous maps in the $\mathcal {C}^k$ topology.(b)
$f$ is homotopic to a $k$-regulous map.
Up to now, Corollary 1.4 with 
$X$ compact and 
$\dim X \geq p \geq 1$ has only been known for three special values of 
$p$, namely, 
$p=1,2$ or 
$4$ [Reference KucharzKuc09, Corollary 3.8]. Since 
$\infty$-regulous is the same as regular, the value 
$k=\infty$ is allowed in Corollary 1.4 according to [Reference Bochnak and KucharzBK22, Corollary 1.2].
In Theorem 1.2 and Corollary 1.4 the integer 
$k$ is assumed to be positive, that is, the case 
$k=0$ is excluded (which perhaps is not necessary). However, we have the following criterion involving nice regulous maps, which are 
$0$-regulous by definition.
Corollary 1.5 Let 
$X$ be a compact nonsingular real algebraic variety and let 
$k$, 
$p$ be two nonnegative integers. Assume that a 
$\mathcal {C}^{\infty }$ map 
$f \colon X \to \mathbb {S}^p$ is homotopic to a nice regulous map. Then 
$f$ can be approximated by 
$k$-regulous maps in the 
$\mathcal {C}^k$ topology.
Proof. To deal with the case 
$k=0$ we choose an integer 
$l > k$. Since 
$f$ is homotopic to a nice regulous map, it is also homotopic to a nice 
$l$-regulous map [Reference KucharzKuc09, Theorem 2.4]. Therefore, by Corollary 1.4, 
$f$ can be approximated by 
$l$-regulous maps in the 
$\mathcal {C}^l$ topology. The conclusion follows.
In connection with Corollary 1.5, it is natural to raise the question whether every regulous map from 
$X$ into 
$\mathbb {S}^p$ is homotopic to a nice regulous map. According to [Reference KucharzKuc09, Theorem 2.4], the continuous maps into unit spheres that are homotopic to nice regulous maps are characterized in terms of framed cobordism classes via the Pontryagin–Thom construction. Next we focus on approximation by nice 
$k$-regulous maps.
Let 
$X$ be a nonsingular real algebraic variety. If 
$Z$ is a nonsingular Zariski locally closed subset of 
$X$, then its Zariski closure 
$V$ in 
$X$ is of the form 
$V=Z \cup W$, where 
$W$ is a Zariski closed subset of 
$X$ with 
$Z \cap W = \varnothing$ and 
$\dim W < \dim Z$. Clearly, 
$Z$ is precisely the nonsingular locus of 
$V$, assuming that 
$Z$ is closed in 
$X$ (in the Euclidean topology). An illustrative example is provided by 
$Z=C \setminus \{(0:0:1)\}$, where 
$C$ is the singular cubic curve
\[ C := \{ (x:y:z) \in \mathbb{P}^2(\mathbb{R}) : y^2z - x^3 - x^2z = 0 \} \]
in the real projective plane 
$\mathbb {P}^2(\mathbb {R})$.
A compact 
$\mathcal {C}^{\infty }$ submanifold 
$M$ of 
$X$ is said to admit a weak algebraic approximation if, for every neighborhood 
$\mathcal {U}$ of the inclusion map 
$M \hookrightarrow X$ in the space 
$\mathcal {C}^{\infty }(M,X)$, there exists a 
$\mathcal {C}^{\infty }$ embedding 
$e \colon M \to X$ in 
$\mathcal {U}$ such that 
$e(M)$ is a nonsingular Zariski locally closed subset of 
$X$.
Assume that 
$X$ is compact. A 
$\mathcal {C}^{\infty }$ map 
$f \colon X \to \mathbb {S}^p$ is said to be adapted (respectively, weakly adapted) if there exists a regular value 
$y \in \mathbb {S}^p$ for 
$f$ such that 
$f^{-1}(y)$ is a nonsingular Zariski locally closed subset of 
$X$ (respectively, the 
$\mathcal {C}^{\infty }$ submanifold 
$f^{-1}(y)$ of 
$X$ admits a weak algebraic approximation).
Our main result on approximation of 
$\mathcal {C}^{\infty }$ maps into unit spheres by nice 
$k$-regulous maps is the following theorem.
Theorem 1.6 Let 
$X$ be a compact nonsingular real algebraic variety and let 
$k$, 
$p$ be two integers, with 
$k \geq 0$, 
$p \geq 1$. Then, for a 
$\mathcal {C}^{\infty }$ map 
$f \colon X \to \mathbb {S}^p$, the following conditions are equivalent.
(a)
$f$ can be approximated by nice $k$-regulous maps in the $\mathcal {C}^k$ topology.(b)
$f$ can be approximated by adapted $\mathcal {C}^{\infty }$ maps in the $\mathcal {C}^k$ topology.(c)
$f$ can be approximated by weakly adapted $\mathcal {C}^{\infty }$ maps in the $\mathcal {C}^k$ topology.
Using Theorem 1.6, we can obtain two approximation results that do not require any technical assumptions.
Corollary 1.7 Let 
$X$ be a compact nonsingular real algebraic variety of dimension 
$p$ and let 
$k$ be a nonnegative integer. Then every 
$\mathcal {C}^{\infty }$ map from 
$X$ into 
$\mathbb {S}^p$ can be approximated by nice 
$k$-regulous maps in the 
$\mathcal {C}^k$ topology.
Proof. Since 
$\dim X = p$, every 
$\mathcal {C}^{\infty }$ map from 
$X$ into 
$\mathbb {S}^p$ is adapted, and hence the conclusion follows from Theorem 1.6.
For maps between unit spheres we have the following theorem.
Theorem 1.8 Let 
$k$ be a nonnegative integer. Then, for every pair 
$(n,p)$ of nonnegative integers, every 
$\mathcal {C}^{\infty }$ map from 
$\mathbb {S}^n$ into 
$\mathbb {S}^p$ can be approximated by nice 
$k$-regulous maps in the 
$\mathcal {C}^k$ topology.
Proof. Let 
$M$ be a compact 
$\mathcal {C}^{\infty }$ submanifold of 
$\mathbb {S}^n$ with 
$\dim M < n$. Let 
$a$ be a point in 
$\mathbb {S}^n \setminus M$ and let 
$\rho \colon \mathbb {S}^n \setminus \{a\} \to \mathbb {R}^n$ be the stereographic projection. By [Reference Akbulut and KingAK92, Theorem A], the 
$\mathcal {C}^{\infty }$ submanifold 
$\rho (M)$ of 
$\mathbb {R}^n$ admits a weak algebraic approximation. Since 
$\rho$ is a biregular isomorphism, 
$M$ admits a weak algebraic approximation in 
$\mathbb {S}^n$. Consequently, if 
$p\geq 1$, then every 
$\mathcal {C}^{\infty }$ map 
$\mathbb {S}^n \to \mathbb {S}^p$ is weakly adapted, and hence the conclusion follows by Theorem 1.6. The case 
$p=0$ is trivial.
It remains undecided whether or not for any pair 
$(n,p)$ of nonnegative integers every 
$\mathcal {C}^{\infty }$ map 
$\mathbb {S}^n \to \mathbb {S}^p$ can be approximated by regular maps in the 
$\mathcal {C}^{\infty }$ (or 
$\mathcal {C}^0$) topology (see [Reference Bochnak and KucharzBK22] for more information).
We now turn to a different characterization of the 
$\mathcal {C}^{\infty }$ maps into unit spheres that can be approximated by nice 
$k$-regulous maps.
Let 
$X$ be a compact nonsingular real algebraic variety and let 
$p$ be an integer with 
$0 \leq p \leq n := \dim X$. Following [Reference Kucharz and KurdykaKK16, p. 19], we say that a cohomology class 
$v \in H^p(X; \mathbb {Z}/2)$ is adapted if the homology class in 
$H_{n-p}(X; \mathbb {Z}/2)$ Poincaré dual to 
$v$ can be represented by a compact 
$(n-p)$-dimensional 
$\mathcal {C}^{\infty }$ submanifold 
$Z$ of 
$X$, embedded with trivial normal bundle, such that 
$Z$ is a nonsingular Zariski locally closed subset of 
$X$. Denote by 
$A^p(X; \mathbb {Z}/2)$ the subgroup of 
$H^p(X; \mathbb {Z}/2)$ generated by all adapted cohomology classes.
Theorem 1.9 Let 
$X$ be a compact nonsingular real algebraic variety and let 
$k$, 
$p$ be two integers, with 
$k \geq 0$, 
$2p \geq \dim X + 1$. Then, for a 
$\mathcal {C}^{\infty }$ map 
$f \colon X \to \mathbb {S}^p$, the following conditions are equivalent.
(a)
$f$ can be approximated by nice $k$-regulous maps in the $\mathcal {C}^k$ topology.(b)
$f$ can be approximated by nice regulous maps in the $\mathcal {C}^0$ topology.(c)
$f$ is homotopic to a nice regulous map.(d)
$f^*(\sigma _p) \in A^p(X; \mathbb {Z}/2)$, where $f^* \colon H^p(\mathbb {S}^p; \mathbb {Z}/2) \to H^p(X; \mathbb {Z}/2)$ is the induced homomorphism and $\sigma _p$ is the unique nonzero element in $H^p(\mathbb {S}^p;\mathbb {Z}/2) \cong \mathbb {Z}/2$.
It is natural to wonder whether the assumption 
$2p \geq \dim X + 1$ in Theorem 1.9 is necessary.
The following example sheds light on some relationships between regular, 
$k$-regulous, and 
$\mathcal {C}^{\infty }$ maps with values in unit spheres.
Example 1.10 Let 
$k$ be a nonnegative integer and let 
$\mathbb {T}^n = \mathbb {S}^1 \times \cdots \times \mathbb {S}^1$ be the 
$n$-fold product of 
$\mathbb {S}^1$. One readily checks that 
$A^p(\mathbb {T}^n; \mathbb {Z}/2) = H^p(\mathbb {T}^n; \mathbb {Z}/2)$ for 
$0 \leq p \leq n$. Hence, in view of Theorem 1.9, if 
$2p \geq n+1$, then every 
$\mathcal {C}^{\infty }$ map 
$\mathbb {T}^n \to \mathbb {S}^p$ can be approximated by nice 
$k$-regulous maps in the 
$\mathcal {C}^k$ topology. On the other hand, by [Reference Bochnak and KucharzBK87b, Theorem 3.2], if 
$n$ is a positive even integer, then every regular map 
$\mathbb {T}^n \to \mathbb {S}^n$ is null homotopic (of course, there are 
$\mathcal {C}^{\infty }$ maps 
$\mathbb {T}^n \to \mathbb {S}^n$ that are not null homotopic and they do not admit approximation by regular maps in the 
$\mathcal {C}^0$ topology). In particular, we cannot allow 
$k=\infty$ in Theorems 1.6 and 1.9 and in Corollaries 1.5 and 1.7. Furthermore, according to [Reference KucharzKuc14a, Theorem 2.8], if 
$n > p \geq 1$, then there exist a nonsingular real algebraic variety 
$X$ and a 
$\mathcal {C}^{\infty }$ map 
$f \colon X \to \mathbb {S}^p$ such that 
$X$ is diffeomorphic to 
$\mathbb {T}^n$ and 
$f$ is not homotopic to any regulous map.
There is ample evidence that the phenomenon exhibited in Example 1.10 is quite common: 
$k$-regulous maps, where 
$k$ is a nonnegative integer, are more flexible than regular maps. Approximation by regular maps is investigated in [Reference Benoist and WittenbergBW21, Reference Bochnak and KucharzBK22] and numerous earlier papers [Reference Bochnak and KucharzBK87a, Reference Bochnak and KucharzBK88, Reference Bochnak and KucharzBK89, Reference Bochnak and KucharzBK93, Reference Bochnak and KucharzBK99, Reference Bochnak and KucharzBK10, Reference Bochnak, Kucharz and SilholBKS97, Reference GhiloniGhi06a, Reference GhiloniGhi06b, Reference GhiloniGhi07, Reference IvanovIva82, Reference Joglar-PrietoJog00, Reference Joglar-Prieto and MangolteJM04, Reference KucharzKuc99, Reference KucharzKuc10, Reference MangolteMan06, Reference OzanOza95, Reference OzanOza02].
Theorems 1.2, 1.6 and 1.9 are proved in § 4. The methods employed in the proof of Theorem 1.2 are developed in §§ 2 and 3. The inspiration for these methods originates from complex geometry, especially Gromov's article [Reference GromovGro89] and the related works of Forstnerič and others elaborated in [Reference ForstneričFor17]. Of independent interest are Theorems 3.6, 3.7, 4.2 and 4.3, which are refined versions of Theorem 1.2. We derive Theorem 1.6 by combining Corollary 4.4 with some results of [Reference KucharzKuc09]. For the proof of Theorem 1.9, essential are Theorem 1.6, [Reference Kucharz and KurdykaKK16] and Benoist's paper [Reference BenoistBen20]. The results on maps into unit spheres announced above are significant improvements upon [Reference KucharzKuc14a, Reference KucharzKuc16a, Reference Kucharz and KurdykaKK16], which deal exclusively with approximation by nice regulous maps in the 
$\mathcal {C}^0$ topology.
2. Malleability and local malleability properties
As in [Reference Kucharz and KurdykaKK18a], by a stratification of a real algebraic variety 
$V$ we mean a finite collection 
$\mathcal {V}$ of pairwise disjoint Zariski locally closed subsets whose union is 
$V$. Each element of 
$\mathcal {V}$ is called a stratum; a stratum can be empty.
Definition 2.1 Let 
$k$ be a nonnegative integer or 
$k=\infty$, 
$X$ and 
$Y$ nonsingular real algebraic varieties, 
$\mathcal {X}$ a stratification of 
$X$, and 
$\mathcal {Y}$ a stratification of 
$Y$.
A map 
$f \colon X \to Y$ is said to be 
$(k,\mathcal {X})$-regular if it is of class 
$\mathcal {C}^k$ and for each stratum 
$S \in \mathcal {X}$ the restriction 
$f|_S \colon S \to Y$ is a regular map. If, in addition, 
$f(S)$ is contained in a stratum 
$T \in \mathcal {Y}$, then 
$f$ is said to be 
$(k,\mathcal {X},\mathcal {Y})$-regular.
We are now in a position to give an alternative description of 
$k$-regulous maps (see also [Reference Kollár and NowakKN15, Proposition 8] and [Reference Fichou, Huisman, Mangolte and MonnierFHMM16, Théorème 4.1]).
Lemma 2.2 Let 
$k$, 
$X$, 
$Y$, 
$\mathcal {X}$, 
$\mathcal {Y}$ be as in Definition 2.1.
(i) If a map
$f \colon X \to Y$ is $(k,\mathcal {X})$-regular, then it is $k$-regulous.(ii) If a map
$f \colon X \to Y$ is $k$-regulous, then there exists a stratification $\mathcal {X}'$ of $X$ such that $X \setminus P(f)$ is a stratum of $\mathcal {X}'$ and $f$ is $(k, \mathcal {X}')$-regular ($P(f)$ is the Zariski closed subset of $X$ defined in § 1).(iii) If a map
$f \colon X \to Y$ is $k$-regulous, then there exists a stratification $\mathcal {X}''$ of $X$ such that $f$ is $(k, \mathcal {X}'', \mathcal {Y})$-regular.
Proof. The proof of (i) is straightforward, and (ii) follows from [Reference Kollár and NowakKN15, Proposition 8 and p. 91] ([Reference Kollár and NowakKN15] deals with 
$Y=\mathbb {R}$, but the general case follows at once because 
$Y$ can be regarded as a subvariety of 
$\mathbb {R}^p$, for some 
$p$). To prove (iii), we choose a stratification 
$\mathcal {X}'$ as in (ii), and define
\[ \mathcal{X}'' := \{(f|_S)^{-1}(T) : S \in \mathcal{X}' \text{ and } T \in \mathcal{Y}\}. \]
For the sake of clarity, we record the following corollary (see also [Reference Fichou, Huisman, Mangolte and MonnierFHMM16, Corollaire 4.14]).
Corollary 2.3 Let 
$X$, 
$Y$, 
$Z$ be nonsingular real algebraic varieties, and 
$k$ a nonnegative integer or 
$k=\infty$. Assume that 
$f \colon X \to Y$ and 
$g \colon Y \to Z$ are 
$k$-regulous maps. Then the composite map 
$g \circ f$ is also 
$k$-regulous.
Proof. By Lemma 2.2(ii), there exists a stratification 
$\mathcal {Y}$ of 
$Y$ such that the map 
$g$ is 
$(k, \mathcal {Y})$-regular. In view of Lemma 2.2(iii), we can choose a stratification 
$\mathcal {X}$ of 
$X$ such that the map 
$f$ is 
$(k, \mathcal {X}, \mathcal {Y})$-regular. Consequently, the map 
$g \circ f$ is 
$(k, \mathcal {X})$-regular, so it is 
$k$-regulous by Lemma 2.2(i).
In what follows we work with vector bundles, which are always 
$\mathbb {R}$-vector bundles. Let 
$Y$ be a real algebraic variety. Given a vector bundle 
$p \colon E \to Y$ over 
$Y$, with total space 
$E$ and bundle projection 
$p$, we sometimes refer to 
$E$ as a vector bundle over 
$Y$. If 
$y$ is a point in 
$Y$, we let 
$E_y := p^{-1}(y)$ denote the fiber of 
$E$ over 
$y$ and write 
$0_y$ for the zero vector in 
$E_y$. We call the set 
$Z(E) := \{0_y \in E : y \in Y\}$ the zero section of 
$E$.
For the general theory of algebraic vector bundles over real algebraic varieties we refer the reader to [Reference Bochnak, Coste and RoyBCR98, § 12.1]. For each algebraic vector bundle 
$E$ over 
$Y$ there exist a nonnegative integer 
$n$ and a surjective algebraic morphism from the product vector bundle 
$Y \times \mathbb {R}^n$ onto 
$E$ [Reference Bochnak, Coste and RoyBCR98, Theorem 12.1.7].
Assuming that 
$Y$ is a nonsingular real algebraic variety, we write 
$TY$ for the tangent bundle to 
$Y$, and 
$T_yY$ for the tangent space to 
$Y$ at 
$y \in Y$.
The following notions will be crucial in the proofs of all our main theorems.
Definition 2.4 Let 
$Y$ be a nonsingular real algebraic variety, and 
$k$ a positive integer or 
$k=\infty$.
(i) A
$k$-regulous spray for $Y$ is a triple $(E, p, s)$, where $p \colon E \to Y$ is an algebraic vector bundle over $Y$ and $s \colon E \to Y$ is a $k$-regulous map such that $s(0_y) = y$ for all $y \in Y$.(ii) A
$k$-regulous spray $(E, p, s)$ for $Y$ is said to be dominating if the derivative
maps the subspace\[ {d_{0_y}s \colon T_{0_y}E \to T_yY} \]
$E_y = T_{0_y}E_y$ of $T_{0_y}E$ onto $T_yY$, that is,
\[ d_{0_y}s(E_y) = T_y Y \quad \text{for all } y \in Y. \]
(iii) The variety
$Y$ is called $k$-malleable if it admits a dominating $k$-regulous spray.
For simplicity, 
$\infty$-regulous sprays, dominating 
$\infty$-regulous sprays and 
$\infty$-malleable varieties are called sprays, dominating sprays and malleable varieties, respectively.
Since 
$\infty$-regulous maps are regular, it follows that the concepts of spray, dominating spray, and malleable variety in Definition 2.4 above are identical with those in [Reference Bochnak and KucharzBK22, Definition 2.1].
Lemma 2.5 Let 
$Y$ be a nonsingular real algebraic variety, and 
$k$ a positive integer or 
$k=\infty$. If the variety 
$Y$ is 
$k$-malleable, then it admits a dominating 
$k$-regulous spray 
$(E,p,s)$ such that 
$p \colon E = Y \times \mathbb {R}^n \to Y$ is the product vector bundle.
Proof. Let 
$(\tilde {E}, \tilde {p}, \tilde {s})$ be a dominating 
$k$-regulous spray for 
$Y$. Choose a nonnegative integer 
$n$ and a surjective algebraic morphism 
$\alpha \colon E \to \tilde {E}$ from the product vector bundle 
$p \colon E = Y \times \mathbb {R}^n \to Y$ onto 
$\tilde {p} \colon \tilde {E} \to Y$. By Corollary 2.3, the map 
$s \colon E \to Y$, 
$s(y,v) = \tilde {s} (\alpha (y,v))$ is 
$k$-regulous, so 
$(E,p,s)$ is a dominating 
$k$-regulous spray for 
$Y$.
We now recall important examples of malleable real algebraic varieties.
Example 2.6 Let 
$G$ be a linear real algebraic group, that is, a Zariski closed subgroup of the general linear group 
$\mathrm {GL}_n(\mathbb {R})$, for some 
$n$. A 
$G$-space is a real algebraic variety 
$Y$ on which 
$G$ acts, the action 
$G \times Y \to Y$, 
$(a,y) \mapsto a \cdot y$ being a regular map. We say that a 
$G$-space 
$Y$ is good if 
$Y$ is nonsingular and for every point 
$y \in Y$ the derivative of the map 
$G \to Y$, 
$a \mapsto a \cdot y$ at the identity element of 
$G$ is surjective. Clearly, if 
$Y$ is homogeneous for 
$G$ (that is, 
$G$ acts transitively on 
$Y$), then 
$Y$ is a good 
$G$-space. By [Reference Bochnak and KucharzBK22, Proposition 2.8], each good 
$G$-space is malleable.
In particular, the unit 
$n$-sphere 
$\mathbb {S}^n$ and real projective 
$n$-space 
$\mathbb {P}^n(\mathbb {R})$ are malleable varieties, being homogeneous spaces for the orthogonal group 
$\mathrm {O}(n+1) \subset \mathrm {GL}_{n+1}(\mathbb {R})$.
It is also convenient to introduce the following definition.
Definition 2.7 Let 
$Y$ be a nonsingular real algebraic variety.
(i) A local spray for
$Y$ is a regular map $\sigma \colon U \times \mathbb {R}^n \to Y$, where $U$ is a Zariski open subset of $Y$ and $n$ is a nonnegative integer, such that $\sigma (y,0) = y$ for all $y \in U$.(ii) A local spray
$\sigma \colon U \times \mathbb {R}^n \to Y$ for $Y$ is said to be dominating if for every point $y \in U$ the derivative of the map $\sigma (y, \cdot ) \colon \mathbb {R}^n \to Y$, $v \mapsto \sigma (y,v)$ at $0 \in \mathbb {R}^n$ is surjective.(iii) The variety
$Y$ is called locally malleable if for every point $p \in Y$ there exists a dominating local spray $\sigma \colon U \times \mathbb {R}^n \to Y$ for $Y$ with $p \in U$.
It follows directly from Definitions 2.4 and 2.7 that each malleable real algebraic variety is locally malleable. It is plausible that the converse also holds, but we can only prove the following weaker result.
Proposition 2.8 Let 
$Y$ be a locally malleable nonsingular real algebraic variety. Then, for each positive integer 
$k$, the variety 
$Y$ is 
$k$-malleable.
Proof. Since the variety 
$Y$ is quasi-compact in the Zariski topology, there exists a finite collection 
$\{\sigma _i \colon U_i \times \mathbb {R}^{n_i} \to Y : i=1,\ldots,q\}$ of dominating local sprays for 
$Y$ such that the Zariski open sets 
$U_i$ are nonempty and cover 
$Y$. Choose a regular function 
$\varphi _i \colon Y \to \mathbb {R}$ with 
$\varphi _i^{-1}(0) = Y \setminus U_i$ for 
$i=1,\ldots,q$.
Let 
$k$ be a positive integer. By Lemma 2.9 below, there exists a positive integer 
$r$ such that for 
$i=1,\ldots,q$ the map 
$\sigma _i^{(r)} \colon Y \times \mathbb {R}^{n_i} \to Y$ defined by
\[ \sigma_i^{(r)}(y,v_i) = \begin{cases} \sigma_i(y, \varphi_i(y)^r v_i) & \text{for } (y,v_i) \in U_i \times \mathbb{R}^{n_i}\\ y & \text{for } (y,v_i) \in (Y \setminus U_i) \times \mathbb{R}^{n_i} \end{cases} \]
is 
$k$-regulous. Moreover, by construction, for every point 
$y \in U_i$ the derivative of the map 
$\sigma _i^{(r)}(y,\cdot ) \colon \mathbb {R}^{n_i} \to Y$, 
$v_i \mapsto \sigma _i^{(r)}(y,v_i)$ at 
$0 \in \mathbb {R}^{n_i}$ is surjective. For 
$i=1,\ldots,q$, we define recursively a map 
$s_i \colon Y \times \mathbb {R}^{n_1} \times \cdots \times \mathbb {R}^{n_i} \to Y$ by
\[ \begin{array}{ll} s_i = \sigma_1^{(r)} & \text{for } i=1,\\ s_i(y, v_1, \ldots, v_{i-1}, v_i) = \sigma_i^{(r)} (s_{i-1}(y, v_1, \ldots, v_{i-1}), v_i) & \text{for } i \geq 2. \end{array} \]
By Corollary 2.3, the maps 
$s_i$ are 
$k$-regulous. We obtain a dominating 
$k$-regulous spray 
$(E, p, s)$ for 
$Y$, where
\[ p \colon E = Y \times \mathbb{R}^{n_1} \times \cdots \times \mathbb{R}^{n_q} \to Y \]
is the product vector bundle and 
$s = s_q$. Thus, the variety 
$Y$ is 
$k$-malleable.
In the proof of Proposition 2.8 we invoked the following lemma.
Lemma 2.9 Let 
$Y$ be a nonsingular real algebraic variety, 
$U$ a nonempty Zariski open subset of 
$Y$, and 
$\tau \colon U \times \mathbb {R}^n \to Y$ a regular map satisfying 
$\tau (y,0)=y$ for all 
$y\in U$. Let 
$\varphi \colon Y \to \mathbb {R}$ be a regular function with 
$\varphi ^{-1}(0) = Y \setminus U$. Then, for each nonnegative integer 
$k$, there exists a positive integer 
$r(k)$ such that for every integer 
$r \geq r(k)$ the map 
$\tau ^{(r)} \colon Y \times \mathbb {R}^n \to Y$ defined by
\[ \tau^{(r)}(y,w) = \begin{cases} \tau(y, \varphi(y)^r w) & \text{for } (y,w) \in U \times \mathbb{R}^n\\ y & \text{for } (y,w) \in (Y \setminus U) \times \mathbb{R}^n \end{cases} \]
is 
$k$-regulous.
Proof. We may assume that 
$Y$ is an algebraic subset of 
$\mathbb {R}^m$. Then
\[ \tau(y,w) = (\tau_1(y,w), \ldots, \tau_m(y,w)) \quad \text{for all } (y,w) \in U \times \mathbb{R}^n, \]
where the 
$\tau _i \colon U \times \mathbb {R}^n \to \mathbb {R}$ are regular functions for 
$i=1,\ldots,m$. Note that
\[ \tau_i(y,0) = y_i \quad \text{for all } y=(y_1, \ldots, y_m) \in U. \]
By [Reference Bochnak, Coste and RoyBCR98, Proposition 3.2.3], there exist polynomial functions 
$p_i, q_i \colon \mathbb {R}^m \times \mathbb {R}^n \to \mathbb {R}$ such that
\[ q_i^{-1}(0) \cap (U \times \mathbb{R}^n) = \varnothing \quad \text{and} \quad \tau_i(y,w) = \frac{p_i(y,w)}{q_i(y,w)} \quad \text{for all } (y,w) \in U \times \mathbb{R}^n. \]
We get
\[ \tau_i(y,w) - \tau_i(y,0) = \frac{p_i(y,w) q_i(y,0) - p_i(y,0) q_i(y,w)}{q_i(y,w) q_i(y,0)} \]
and hence
\[ \tau_i(y,w) = y_i + \sum_{j=1}^n \tau_{ij}(y,w)w_j, \]
where the 
$\tau _{ij} \colon U \times \mathbb {R}^n \to \mathbb {R}$ are regular functions and 
$w = (w_1, \ldots, w_n)$.
Let 
$k$ be a nonnegative integer and let 
$\pi \colon Y \times \mathbb {R}^n \to Y$ be the canonical projection. Since 
$(\varphi \circ \pi )^{-1}(0) = (Y \times \mathbb {R}^n) \setminus (U \times \mathbb {R}^n)$, there exists a positive integer 
$r(k)$ such that for each integer 
$r \geq r(k)$ the functions 
$\tau _{ij}^{(r)} \colon Y \times \mathbb {R}^n \to \mathbb {R}$ defined by
\[ \tau_{ij}^{(r)}(y,w) = \begin{cases} \tau_{ij}(y,w)\varphi(y)^r & \text{for } (y,w) \in U \times \mathbb{R}^n\\ 0 & \text{for } (y,w) \in (Y \times \mathbb{R}^n) \setminus (U \times \mathbb{R}^n) \end{cases} \]
are of class 
$\mathcal {C}^k$ for 
$i=1,\ldots,m$, 
$j=1,\ldots,n$ (see [Reference KucharzKuc17, Proposition 3.4], and also [Reference Fichou, Huisman, Mangolte and MonnierFHMM16, Lemma 5.2] for 
$Y=\mathbb {R}^m$). Now we define a map 
$\tau ^{(r)} \colon Y \times \mathbb {R}^n \to \mathbb {R}^m$ by
\[ \tau^{(r)}(y,w) = (\tau_1^{(r)}(y,w), \ldots, \tau_m^{(r)}(y,w)), \]
where
\[ \tau_i^{(r)}(y,w) = y_i + \sum_{j=1}^n \tau_{ij}^{(r)}(y, \varphi(y)^rw) w_j \quad \text{for } i=1,\ldots,m. \]
By construction, the map 
$\tau ^{(r)}$ is of class 
$\mathcal {C}^k$. Furthermore,
\[ \tau^{(r)}(y,w)= \begin{cases} \tau(y, \varphi(y)^r w) & \text{for } (y,w) \in U\times \mathbb{R}^n\\ y & \text{for } (y,w) \in (Y \setminus U) \times \mathbb{R}^n. \end{cases} \]
The proof is complete because the restrictions of 
$\tau ^{(r)}$ to 
$U \times \mathbb {R}^n$ and 
$(Y \setminus U) \times \mathbb {R}^n$ are regular maps.
Further study is needed to reveal the relationship between uniform rationality and 
$k$-malleability.
We consider 
$\mathbb {R}^n$ endowed with the Euclidean norm 
$\lVert - \rVert$. If 
$A$ is a nonempty subset of 
$\mathbb {R}^n$ and 
$x \in \mathbb {R}^n$, we write 
$\operatorname {dist}(x,A)$ for the Euclidean distance from 
$x$ to 
$A$.
Lemma 2.10 Let 
$X$ be a real algebraic variety, 
$n$ a nonnegative integer, and 
$U$ a Zariski open neighborhood of 
$X \times \{0\}$ in 
$X \times \mathbb {R}^n$. Then there exists a regular function 
$\varepsilon \colon X \to \mathbb {R}$ such that
\[ \varepsilon(x) > 0 \quad \text{and} \quad \bigg(x, \varepsilon(x) \frac{v}{1 + \lVert v \rVert^2}\bigg) \in U \quad \text{for all }(x,v) \in X \times \mathbb{R}^n. \]
Proof. We may assume that 
$X$ is an algebraic subset of 
$\mathbb {R}^m$ and 
$U \neq X \times \mathbb {R}^n$. Then we choose a polynomial function 
$\eta \colon \mathbb {R}^m \times \mathbb {R}^n \to \mathbb {R}$ such that 
$\eta (x,v) \geq 0$ for all 
$(x,v) \in \mathbb {R}^m \times \mathbb {R}^n$ and the zero set of 
$\eta$ is the algebraic subset 
$Z := (X \times \mathbb {R}^n) \setminus U$ of 
$\mathbb {R}^m \times \mathbb {R}^n$. Since the distance function
\[ \mathbb{R}^m \times \mathbb{R}^n \to \mathbb{R}, \quad (x,v) \mapsto \operatorname{dist}((x,v),Z) \]
is a continuous semialgebraic function whose zero set is 
$Z$, by [Reference Bochnak, Coste and RoyBCR98, Theorem 2.6.6], there exist a positive integer 
$N$ and a continuous semialgebraic function 
$h \colon \mathbb {R}^m \times \mathbb {R}^n \to \mathbb {R}$ such that
\[ \eta(x,v)^N = h(x,v) \operatorname{dist}((x,v), Z) \quad \text{for all } (x,v) \in \mathbb{R}^m \times \mathbb{R}^n. \]
Thus, according to [Reference Bochnak, Coste and RoyBCR98, Proposition 2.6.2], there exist a real constant 
$c > 0$ and a positive integer 
$r$ such that
\[ \lvert h(x,v) \rvert \leq c(1 + \lVert (x,v) \rVert^2)^r \quad \text{for all } (x,v) \in \mathbb{R}^m \times \mathbb{R}^n. \]
Consequently,
\[ \eta(x,0)^N \leq c(1 + \lVert x \rVert^2)^r \operatorname{dist}((x,0), Z) \quad \text{for all } x \in X. \]
It follows that the function 
$\varepsilon \colon X \to \mathbb {R}$ defined by
\[ \varepsilon(x) = \frac{\eta(x,0)^N}{2c(1 + \lVert x \rVert^2)^r} \quad \text{for all } x \in X \]
has the required properties.
Proposition 2.11 Let 
$Y$ be a malleable nonsingular real algebraic variety. Then every Zariski open subset 
$Y_0$ of 
$Y$ is a malleable variety.
Proof. By Lemma 2.5, there exists a spray 
$(E,p,s)$ for 
$Y$ such that 
$p \colon E = Y \times \mathbb {R}^n \to Y$ is the product vector bundle. Let 
$p_0 \colon E_0= Y_0 \times \mathbb {R}^n \to Y_0$ be the product vector bundle over 
$Y_0$. Note that the set 
$U := E_0 \cap s^{-1}(Y_0)$ is a Zariski open neighborhood of 
$Y_0 \times \{0\}$ in 
$E_0$. By Lemma 2.10, there exists a regular function 
$\varepsilon \colon Y_0 \to \mathbb {R}$ such that
\[ \varepsilon(y) > 0 \quad \text{and} \quad \bigg(y, \varepsilon(y) \frac{v}{1 + \lVert v \rVert^2}\bigg) \in U \quad \text{for all } (y,v) \in E_0. \]
Obviously, the map
\[ s_0 \colon Y_0 \times \mathbb{R}^n \to Y_0, \quad (y,v) \mapsto s\bigg(y, \varepsilon(y) \frac{v}{1 + \lVert v \rVert^2}\bigg) \]
is regular. Since the derivative of the map
\[ \mathbb{R}^n \to \mathbb{R}^n, \quad v \mapsto \frac{v}{1 + \lVert v \rVert^2} \]
at 
$0 \in \mathbb {R}^n$ is an isomorphism, it follows that 
$(E_0, p_0, s_0)$ is a dominating spray for 
$Y_0$. Thus, 
$Y_0$ is a malleable variety.
Proposition 2.11 is a rich source of new examples of malleable real algebraic varieties.
Example 2.12 Let 
$Y$ be a real algebraic variety that is a homogeneous space for some linear real algebraic group. As recalled in Example 2.6, 
$Y$ is a malleable variety. Thus, by Proposition 2.11, every Zariski open subset of 
$Y$ is a malleable variety.
Proposition 2.13 Every uniformly rational real algebraic variety is locally malleable.
Proof. According to Definition 1.1, it suffices to prove that every Zariski open subset of 
$\mathbb {R}^n$ is a malleable variety. This follows immediately from Proposition 2.11 because 
$\mathbb {R}^n$ is a malleable variety (to see that 
$\mathbb {R}^n$ is malleable, consider the map 
$\mathbb {R}^n \times \mathbb {R}^n \to \mathbb {R}^n$, 
${(y,v) \mapsto y+v}$).
Corollary 2.14 Let 
$k$ be a positive integer. Every uniformly rational real algebraic variety is 
$k$-malleable.
3. Sections of malleable submersions
We will use freely terminology and notation introduced in § 2.
Notation 3.1 Let 
$X$, 
$Z$ be nonsingular real algebraic varieties, and let 
$h \colon Z \to X$ be a regular map that is a surjective submersion. Furthermore, let 
$V(h)$ denote the algebraic vector subbundle of the tangent bundle 
$TZ$ to 
$Z$ defined by
\[ V(h)_z = \operatorname{Ker}(d_z h \colon T_zZ \to T_{h(z)}X) \quad \text{for all } z \in Z, \]
where 
$d_z h$ is the derivative of 
$h$ at 
$z$. Clearly, 
$V(h)_z$ is the tangent space to the fiber 
$h^{-1}(h(z))$.
Let 
$k$ be a nonnegative integer or 
$k=\infty$, 
$U$ an open subset of 
$X$, and 
$\mathcal {X}$ a stratification of 
$X$. A map 
$f \colon U \to Z$ is called a section (over 
$U$) of 
$h \colon Z \to X$ if 
$h(f(x))=x$ for all 
$x \in U$. A section that is a 
$\mathcal {C}^k$ map is called a 
$\mathcal {C}^k$ section. By a homotopy of 
$\mathcal {C}^k$ sections we mean a continuous map 
$F \colon U \times [0,1] \to Z$ such that 
$F_t \colon U \to Z$, 
$x \mapsto F(x,t)$ is a 
$\mathcal {C}^k$ section for every 
$t \in [0,1]$. Two 
$\mathcal {C}^k$ sections 
$f_0,f_1 \colon U \to Z$ are said to be homotopic through 
$\mathcal {C}^k$ sections if there exists a homotopy 
$F \colon U \times [0,1] \to Z$ of 
$\mathcal {C}^k$ sections with 
$F_0=f_0$ and 
$F_1=f_1$. A global section 
$g \colon X \to Z$ that is a 
$k$-regulous (respectively, 
$(k,\mathcal {X})$-regular) map is called a 
$k$-regulous (respectively, 
$(k,\mathcal {X})$-regular) section. We say that a 
$\mathcal {C}^k$ section 
$f \colon U \to Z$ can be approximated by global 
$k$-regulous (respectively, global 
$(k,\mathcal {X})$-regular) sections in the 
$\mathcal {C}^k$ topology if for every neighborhood 
$\mathcal {U}$ of 
$f$ in the space 
$\mathcal {C}^k(U,Z)$ of all 
$\mathcal {C}^k$ maps there exists a global 
$k$-regulous (respectively, global 
$(k,\mathcal {X})$-regular) section 
$g \colon X \to Z$ such that 
$g|_U$ belongs to 
$\mathcal {U}$. To study approximation by global 
$k$-regulous or global 
$(k,\mathcal {X})$-regular sections, we need several notions and auxiliary results.
Definition 3.2 Let 
$h \colon Z \to X$ be the submersion of Notation 3.1, and 
$k$ a positive integer or 
$k=\infty$.
(i) A
$k$-regulous spray for $h \colon Z \to X$ is a triple $(E,p,s)$, where $p \colon E \to Z$ is an algebraic vector bundle over $Z$ and $s \colon E \to Z$ is a $k$-regulous map such that
\[ s(E_z) \subseteq h^{-1}(h(z)) \quad \text{and} \quad s(0_z)=z \quad \text{for all } z \in Z. \]
(ii) A
$k$-regulous spray $(E,p,s)$ for $h \colon Z \to X$ is said to be dominating if the derivative $d_{0_z}s \colon T_{0_z}E \to T_zZ$ maps the subspace $E_z = T_{0_z}E_z$ of $T_{0_z}E$ onto $V(h)_z$, that is,
\[ d_{0_z}s(E_z) = V(h)_z \quad \text{for all } z \in Z. \]
(iii) The submersion
$h \colon Z \to X$ is called $k$-malleable if it admits a dominating $k$-regulous spray.
For simplicity, 
$\infty$-regulous sprays, dominating 
$\infty$-regulous sprays and 
$\infty$-malleable submersions are called sprays, dominating sprays and malleable submersions, respectively.
Note that if 
$X$ is reduced to a point, then Definition 3.2 coincides with Definition 2.4. Since 
$\infty$-regulous maps are regular, it follows that the concepts of spray, dominating spray, and malleable submersion in Definition 3.2 above are identical with those in [Reference Bochnak and KucharzBK22, Definition 3.2]. Basic properties of dominating sprays for 
$h \colon Z \to X$ are established in [Reference Bochnak and KucharzBK22, § 3]. Taking into account all the necessary modifications, in the next lemmas we prove analogous results for 
$k$-regulous sprays.
Lemma 3.3 Let 
$h\colon Z \to X$ be the submersion of Notation 3.1, and 
$k$ a positive integer or 
$k=\infty$. If the submersion 
$h\colon Z \to X$ is 
$k$-malleable, then it admits a dominating 
$k$-regulous spray 
$(E,p,s)$ such that 
$p \colon E = Z \times \mathbb {R}^n \to Z$ is the product vector bundle.
Proof. Let 
$(\tilde {E}, \tilde {p}, \tilde {s})$ be a dominating 
$k$-regulous spray for 
$h \colon Z \to X$. Choose a nonnegative integer 
$n$ and a surjective algebraic morphism 
$\alpha \colon E \to \tilde {E}$ from the product vector bundle 
$p \colon E = Z \times \mathbb {R}^n \to Z$ onto 
$\tilde {p} \colon \tilde {E} \to Z$. By Corollary 2.3, the map 
$s \colon E \to Z$, 
$s(z,v) = \tilde {s}(\alpha (z,v))$ is regulous, so 
$(E,p,s)$ is a dominating 
$k$-regulous spray for 
$h \colon Z \to X$.
Lemma 3.4 Let 
$h\colon Z \to X$ be the submersion of Notation 3.1, and 
$k$ a positive integer or 
$k=\infty$. Suppose that 
$(E,p,s)$ is a dominating 
$k$-regulous spray for 
$h \colon Z \to X$. Let 
$U$ be an open subset of 
$X$ and let 
$F \colon U \times [0,1] \to Z$ be a homotopy of 
$\mathcal {C}^k$ sections of 
$h \colon Z \to X$. Let 
$U_0$ be an open subset of 
$X$ whose closure 
$\overline {U}_0$ is compact and contained in 
$U$. Let 
$t_0$ be a point in 
$[0,1]$. Then there exist a neighborhood 
$I_0$ of 
$t_0$ in 
$[0,1]$ and a continuous map 
$\xi \colon U_0 \times I_0 \to E$ such that
(3.4.1)
$p(\xi (x,t)) = F(x,t_0)$ for all $(x,t) \in U_0 \times I_0$,(3.4.2)
$\xi (x,t_0) = 0_{F(x,t_0)}$ for all $x \in U_0$,(3.4.3)
$s(\xi (x,t)) = F(x,t)$ for all $(x,t) \in U_0 \times I_0$,(3.4.4) for every
$t \in I_0$ the map $U_0 \to E$, $x \mapsto \xi (x,t)$ is of class $\mathcal {C}^k$.
Proof. Consider the 
$\mathcal {C}^{k-1}$ morphism
\[ \alpha \colon E \to V(h), \quad v \mapsto d_{0_{p(v)}} s(v) \]
of algebraic vector bundles (by convention, 
$\infty - 1 = \infty$). Since 
$\alpha$ is a surjective morphism, its kernel 
$K$ is a 
$\mathcal {C}^{k-1}$ vector subbundle of 
$E$. Hence, 
$E$ can be written as the direct sum 
$E = E' \oplus K$ for some 
$\mathcal {C}^{k-1}$ vector subbundle 
$E'$ of 
$E$. The restriction 
$\alpha |_{E'} \colon E' \to V(h)$ is a 
$\mathcal {C}^{k-1}$ isomorphism of vector bundles, so we can choose a 
$\mathcal {C}^{k-1}$ morphism 
$\beta \colon V(h) \to E$ that induces an isomorphism of 
$V(h)$ onto 
$E'$. Let 
$\varphi$ be the global 
$\mathcal {C}^{k-1}$ section of the algebraic vector bundle 
$\operatorname {Hom}(V(h), E)$ that is determined by 
$\beta$. If 
$\psi$ is a 
$\mathcal {C}^k$ section of 
$\operatorname {Hom}(V(h), E)$ sufficiently close to 
$\varphi$ in the strong 
$\mathcal {C}^0$ topology (see [Reference HirschHir97, p. 35] for the definition of the strong 
$\mathcal {C}^0$ topology), then the 
$\mathcal {C}^k$ morphism 
$\gamma \colon V(h) \to E$ corresponding to 
$\psi$ is injective and the image of 
$\gamma$ is a 
$\mathcal {C}^k$ vector subbundle 
$\hat {p} \colon \hat {E} \to Z$ of 
$p \colon E \to Z$ such that 
$E = \hat {E} \oplus K$. By construction, the restriction 
$\alpha |_{\hat {E}} \colon \hat {E} \to V(h)$ is a 
$\mathcal {C}^{k-1}$ isomorphism.
Let 
$f \colon U \to Z$ be a 
$\mathcal {C}^k$ section of 
$h \colon Z \to X$ defined by 
$f(x) = F(x,t_0)$ for all 
$x\in U$. Denote by 
$p_f \colon \hat {E}_f \to U$ the pullback of the vector bundle 
$\hat {p} \colon \hat {E} \to Z$ under the map 
$f$. Recall that 
$p_f \colon \hat {E}_f \to U$ is a 
$\mathcal {C}^k$ vector bundle, where
\[ \hat{E}_f := \{(x,v) \in U \times \hat{E} : f(x) = \hat{p}(v)\}, \quad p_f(x,v) = x. \]
Note that
\[ s_f \colon \hat{E}_f \to Z, \quad s_f(x,v)=s(v) \]
is a 
$\mathcal {C}^k$ map.
Let 
$x \in U$. The zero vector in the fiber 
$(\hat {E}_f)_x$ is 
$(x, 0_{f(x)})$, where 
$0_{f(x)}$ is the zero vector in the fiber 
$\hat {E}_{f(x)}$. Since 
$s_f(x,0_{f(x)}) = s(0_{f(x)}) = f(x)$, it follows that 
$s_f$ induces a 
$\mathcal {C}^k$ diffeomorphism between the zero section 
$Z(\hat {E}_f)$ and 
$f(U)$. Moreover, the derivative
\[ d_{(x, 0_{f(x)})} s_f \colon T_{(x, 0_{f(x)})} \hat{E}_f \to T_{f(x)}Z \]
is an isomorphism because
\[ d_{0_z} s|_{\hat{E}_z} = \alpha|_{\hat{E}_z} \colon \hat{E}_z \to V(h)_z \]
is an isomorphism for all 
$z \in Z$. Consequently, 
$s_f$ is a local diffeomorphism at the point 
$(x,0_{f(x)})$. Thus, by [Reference Bröcker and JänichBJ82, (12.7)], there exist an open neighborhood 
$M \subseteq \hat {E}_f$ of the zero section 
$Z(\hat {E}_f)$ and an open neighborhood 
$N \subseteq Z$ of 
$f(U)$ such that the restriction 
$\sigma \colon M \to N$ of 
$s_f \colon \hat {E}_f \to Z$ is a 
$\mathcal {C}^k$ diffeomorphism.
Since 
$\overline {U}_0$ is a compact subset of 
$U$, we can choose an open neighborhood 
$I_0$ of 
$t_0$ in 
$[0,1]$ such that 
$F_t(\overline {U}_0) \subseteq N$ for all 
$t \in I_0$. Therefore, for each 
$t \in I_0$, there exists a unique 
$\mathcal {C}^k$ map 
$\zeta _t \colon U_0 \to \hat {E}_f$ satisfying 
$\zeta _t(U_0) \subseteq M$ and 
$F_t(x) = \sigma (\zeta _t(x))$ for all 
$x \in U_0$. We have 
$\zeta _t(x) = (\alpha _t(x), \xi _t(x))$, where 
$\alpha _t \colon U_0 \to U$ and 
$\xi _t \colon U_0 \to \hat {E} \subseteq E$ are 
$\mathcal {C}^k$ maps with
\[ f(\alpha_t(x)) = \hat{p}(\xi_t(x)) = p(\xi_t(x)) \quad \text{and} \quad s(\xi_t(x)) = F_t(x). \]
By Definition 3.2(i), 
$s(\xi _t(x)) \in h^{-1}(h(p(\xi _t(x))))$, and hence
\[ h(s(\xi_t(x))) = h(f(\alpha_t(x))) = \alpha_t(x). \]
On the other hand,
\[ h(s(\xi_t(x))) = h(F_t(x)) = x. \]
Consequently, 
$\alpha _t(x)=x$. It follows that 
$\zeta _t \colon U_0 \to \hat {E}_f$ is a 
$\mathcal {C}^k$ section, over 
$U_0$, of the vector bundle 
$p_f \colon \hat {E}_f \to U$. Clearly, 
$\zeta _{t_0}(U_0) \subseteq Z(\hat {E}_f)$. Furthermore, the map
\[ \zeta \colon U_0 \times I_0 \to \hat{E}_f, \quad (x,t) \mapsto \zeta_t(x) \]
is continuous. Note that 
$\zeta (x,t) = (x,\xi (x,t))$, where
\[ \xi \colon U_0 \times I_0 \to \hat{E} \subseteq E, \quad (x,t) \mapsto \xi_t(x) \]
is a continuous map with 
$p(\xi (x,t)) = f(x) = F(x,t_0)$ for all 
$(x,t) \in U_0 \times I_0$. By construction, the map 
$\xi$ satisfies conditions (3.4.1)–(3.4.4).
We now state the following key lemma.
Lemma 3.5 Assume that the submersion 
$h \colon Z \to X$ of Notation 3.1 is 
$k$-malleable, where 
$k$ is a nonnegative integer or 
$k=\infty$. Let 
$U$ be an open subset of 
$X$ and let 
${F \colon U \times [0,1] \to Z}$ be a homotopy of 
$\mathcal {C}^k$ sections of 
$h \colon Z \to X$. Let 
$U_0$ be an open subset of 
$X$ whose closure 
$\overline {U}_0$ is compact and contained in 
$U$. Then there exist a dominating 
$k$-regulous spray 
$(E,p,s)$ for 
$h \colon Z \to X$ and a continuous map 
$\xi \colon U_0 \times [0,1] \to E$ such that 
$p \colon E = Z \times \mathbb {R}^n \to Z$ is the product vector bundle and 
$\xi (x,t) = (F(x,0), \eta (x,t))$ for all 
$(x,t) \in U_0 \times [0,1]$, where the map 
$\eta \colon U_0 \times [0,1] \to \mathbb {R}^n$ satisfies
(3.5.1)
$\eta (x,0)=0$ for all $x \in U_0$,(3.5.2)
$s(F(x,0),\eta (x,t)) = F(x,t)$ for all $(x,t) \in U_0 \times [0,1]$,(3.5.3) for every
$t \in [0,1]$ the map $U_0 \to \mathbb {R}^n$, $x \mapsto \eta (x,t)$ is of class $\mathcal {C}^k$.
Proof. By Lemma 3.3, the submersion 
$h \colon Z \to X$ admits a dominating 
$k$-regulous spray 
$(\tilde {E}, \tilde {p}, \tilde {s})$ such that 
$\tilde {p} \colon \tilde {E} = Z \times \mathbb {R}^m \to Z$ is the product vector bundle. In view of Lemma 3.4 and the compactness of the interval 
$[0,1]$ (see the Lebesgue lemma for compact metric spaces [Reference Bogomolov and BöhningBre93, p. 28, Lemma 9.11]), there exists a partition 
$0=t_0 < t_1 < \cdots < t_r =1$ of 
$[0,1]$ such that for each 
$i=1,\ldots,r$ there exists a continuous map 
$\xi ^i \colon U_0 \times [t_{i-1},t_i] \to \tilde {E}$ with the following properties:
•
$\xi ^i(x,t) = (F(x,t_{i-1}), \eta ^i(x,t))$ for all $(x,t) \in U_0 \times [t_{i-1},t_i]$,•
$\eta ^i(x, t_{i-1}) = 0$ for all $x \in U_0$,•
$\tilde {s}(F(x,t_{i-1}), \eta ^i(x,t)) = F(x,t)$ for all $(x,t) \in U_0 \times [t_{i-1}, t_i]$,• for every
$t \in [t_{i-1}, t_i]$ the map $U_0 \to \mathbb {R}^m$, $x \mapsto \eta ^i(x,t)$ is of class $\mathcal {C}^k$.
For 
$i=1,\ldots,r$ we define recursively a dominating 
$k$-regulous spray 
$(E^{(i)}, p^{(i)}, s^{(i)})$ for 
$h \colon {Z \to X}$ by
\[ (E^{(i)}, p^{(i)}, s^{(i)}) = (\tilde{E}, \tilde{p},\tilde{s}) \quad \text{if } i=1, \]
while for 
$i \geq 2$ we require
\[ p^{(i)} \colon E^{(i)} = Z \times (\mathbb{R}^m)^i \to Z \]
to be the product vector bundle and set
\[ s^{(i)} \colon E^{(i)} \to Z, \quad s^{(i)}(z, v_1,\ldots,v_i) = s^{(1)}(s^{(i-1)}(z, v_1,\ldots,v_{i-1}), v_i), \]
where 
$z \in Z$ and 
$v_1,\ldots,v_i \in \mathbb {R}^m$ (the map 
$s^{(i)}$ is 
$k$-regulous by Corollary 2.3).
In particular, 
$(E,p,s) := (E^{(r)}, p^{(r)}, s^{(r)})$ is a dominating 
$k$-regulous spray for 
${h \colon Z \to X}$. Note that 
$p \colon E = Z \times \mathbb {R}^n \to Z$ is the product vector bundle with 
$\mathbb {R}^n = (\mathbb {R}^m)^r$. Now, consider a map
\[ \xi \colon U_0 \times [0,1] \to E, \quad \xi(x,t) = (F(x,0), \eta(x,t)), \]
where 
$\eta \colon U_0 \times [0,1] \to \mathbb {R}^n = (\mathbb {R}^m)^r$ is defined by
\[ \eta(x,t) = (\eta^1(x,t), 0,\ldots,0) \]
for all 
$(x,t) \in U_0 \times [t_0,t_1]$, and
\[ \eta(x,t) = (\eta^1(x,t_1), \ldots, \eta^{i-1}(x,t_{i-1}), \eta^i(x,t), 0,\ldots, 0) \]
for all 
$(x,t) \in U_0 \times [t_{i-1}, t_i]$ with 
$i=2,\ldots,r$. One readily checks that 
$\eta$ is a well-defined continuous map satisfying (3.5.1)–(3.5.3).
Now we are ready to prove the following approximation result for sections.
Theorem 3.6 Assume that the submersion 
$h\colon Z \to X$ of Notation 3.1 is 
$k$-malleable, where 
$k$ is a nonnegative integer or 
$k=\infty$. Let 
$U$ be an open subset of 
$X$ and let 
$f \colon U \to Z$ be a 
$\mathcal {C}^k$ section of 
$h \colon Z \to X$ that is homotopic through 
$\mathcal {C}^k$ sections to the restriction 
$f_0|_U$ of a global 
$k$-regulous section 
$f_0 \colon X \to Z$. Then 
$f$ can be approximated by global 
$k$-regulous sections.
Proof. Let 
$F \colon U \times [0,1] \to Z$ be a homotopy of 
$\mathcal {C}^k$ sections such that 
$F_0=f_0|_U$ and 
$F_1 = f$. Let 
$U_0$ be an open subset of 
$X$ whose closure 
$\overline {U}_0$ is compact and contained in 
$U$, and let 
$(E,p,s)$, 
$\xi \colon U_0 \times [0,1] \to E$, 
$\xi (x,t) = (F(x,0), \eta (x,t))$, 
${\eta \colon U_0 \times [0,1] \to \mathbb {R}^n}$, be as in Lemma 3.5. In particular, we have
\[ s(f_0(x), \eta(x,1)) = s(F(x,0), \eta(x,1)) = F(x,1) = f(x) \quad \text{for all } x \in U_0. \]
By the Weierstrass approximation theorem, there exists a regular map 
$\beta \colon X \to \mathbb {R}^n$ such that the restriction 
$\beta |_{U_0}$ is arbitrarily close to the 
$\mathcal {C}^k$ map 
$\eta _1 \colon U_0 \to \mathbb {R}^n$, 
$x \mapsto \eta (x,1)$ in the 
$\mathcal {C}^k$ topology. Then
\[ g \colon X \to Z, \quad x \mapsto s(f_0(x), \beta(x)) \]
is a 
$k$-regulous map (by Corollary 2.3) such that 
$g|_{U_0}$ is close to 
$f|_{U_0}$ in the 
$\mathcal {C}^k$ topology. Moreover, in view of Definition 3.2(i), 
$g \colon X \to Z$ is a section of 
$h \colon Z \to X$. The proof is complete because 
$U_0$ is chosen in an arbitrary way.
We also have the following variant of Theorem 3.6.
Theorem 3.7 Assume that the submersion 
$h \colon Z \to X$ of Notation 3.1 is malleable. Let 
$\mathcal {X}$ be a stratification of 
$X$, and 
$k$ a positive integer or 
$k=\infty$. Let 
$U$ be an open subset of 
$X$ and let 
$f \colon U \to Z$ be a 
$\mathcal {C}^k$ section of 
$h \colon Z \to X$ that is homotopic through 
$\mathcal {C}^k$ sections to the restriction 
$f_0|_U$ of a global 
$(k,\mathcal {X})$-regular section 
$f_0 \colon X \to Z$. Then 
$f$ can be approximated by global 
$(k,\mathcal {X})$-regular sections in the 
$\mathcal {C}^k$ topology.
Proof. Let 
$F \colon U \times [0,1] \to Z$ be a homotopy of 
$\mathcal {C}^k$ sections such that 
$F_0=f_0|_U$ and 
$F_1 = f$. Let 
$U_0$ be an open subset of 
$X$ whose closure 
$\overline {U}_0$ is compact and contained in 
$U$, and let 
$(E,p,s)$, 
$\xi \colon U_0 \times [0,1] \to E$, 
$\xi (x,t) = (F(x,0), \eta (x,t))$, 
${\eta \colon U_0 \times [0,1] \to \mathbb {R}^n}$ be as in Lemma 3.5 (with 
$k=\infty$, in which case 
$s \colon E \to X$ is a regular map). In particular, we have
\[ s(f_0(x), \eta(x,1)) = s(F(x,0), \eta(x,1)) = F(x,1) = f(x) \quad \text{for all } x \in U_0. \]
By the Weierstrass approximation theorem, there exists a regular map 
$\beta \colon X \to \mathbb {R}^n$ such that the restriction 
$\beta |_{U_0}$ is arbitrarily close to the 
$\mathcal {C}^k$ map 
$\eta _1 \colon U_0 \to \mathbb {R}^n$, 
$x \mapsto \eta (x,1)$ in the 
$\mathcal {C}^k$ topology. Then
\[ g \colon X \to Z, \quad x \mapsto s(f_0(x), \beta(x)) \]
is a 
$(k, \mathcal {X})$-regular map such that 
$g|_{U_0}$ is close to 
$f|_{U_0}$ in the 
$\mathcal {C}^k$ topology. Moreover, in view of Definition 3.2(i), 
$g \colon X \to Z$ is a section of 
$h \colon Z \to X$. The proof is complete because 
$U_0$ is chosen in an arbitrary way.
The most important special cases of Theorems 3.6 and 3.7 are obtained by taking 
$U=X$.
4. Applications
To discuss applications of Theorems 3.6 and 3.7 we need the following observation.
Lemma 4.1 Let 
$X$, 
$Y$ be nonsingular real algebraic varieties, and 
$k$ a positive integer or 
$k=\infty$. Assume that the variety 
$Y$ is 
$k$-malleable. Then the canonical projection
\[ h \colon X \times Y \to X, \quad (x,y) \mapsto x \]
is a 
$k$-malleable submersion.
Proof. Let 
$(E,p,s)$ be a dominating 
$k$-regulous spray for 
$Y$. We obtain a dominating 
$k$-regulous spray 
$(\tilde {E}, \tilde {p}, \tilde {s})$ for 
$h \colon X \times Y \to X$ setting
\begin{align*} &\tilde{E} = \{ ((x,y),v) \in (X \times Y) \times E : y=p(v)\},\\ &\tilde{p} \colon \tilde{E} \to X \times Y, \quad ((x,y),v) \mapsto (x,y),\\ &\tilde{s} \colon \tilde{E} \to X \times Y, \quad ((x,y),v) \mapsto (x,s(v)). \end{align*}
Theorem 4.2 Let 
$X$, 
$Y$ be nonsingular real algebraic varieties, and 
$k$ a positive integer or 
$k=\infty$. Assume that the variety 
$Y$ is 
$k$-malleable. Then, for a 
$\mathcal {C}^k$ map 
$f \colon X \to Y$, the following conditions are equivalent.
(a)
$f$ can be approximated by $k$-regulous maps in the $\mathcal {C}^k$ topology.(b)
$f$ is homotopic to a $k$-regulous map.
Proof. The implication (a)
$\,\Rightarrow \,$(b) holds because 
$X$ deformation retracts to some compact subset 
$K \subset X$ [Reference Bochnak, Coste and RoyBCR98, Corollary 9.3.7], and any two continuous maps from 
$K$ into 
$Y$ that are sufficiently close in the compact-open topology are homotopic (the latter assertion is valid if 
$Y$ is an arbitrary 
$\mathcal {C}^{\infty }$ manifold).
It remains to prove (b)
$\,\Rightarrow \,$(a). To this end let 
$\Phi \colon X \times [0,1] \to Y$ be a homotopy such that 
$\Phi _0$ is a 
$k$-regulous map and 
$\Phi _1=f$. We may assume that 
$\Phi$ is a 
$\mathcal {C}^k$ map (see [Reference LeeLee03, Proposition 10.22 and its proof]). By Lemma 4.1, the canonical projection 
$h \colon X \times Y \to X$ is 
$k$-malleable. Since
\[ F \colon X \times [0,1] \to X \times Y, \quad (x,t) \mapsto (x, \Phi(x,t)) \]
is a homotopy of 
$\mathcal {C}^k$ sections of 
$h \colon X \times Y \to X$, it follows from Theorem 3.6 that the 
$\mathcal {C}^k$ section
\[ X \to X \times Y, \quad x \mapsto (x,f(x)) \]
can be approximated by 
$k$-regulous sections in the 
$\mathcal {C}^k$ topology, hence (a) holds.
Proof of Theorem 1.2 By Corollary 2.14, the variety 
$Y$ is 
$k$-malleable, so it suffices to apply Theorem 4.2.
Theorem 4.2 not only implies Theorem 1.2, but is in fact more general. Indeed, as recalled in Example 2.6, if 
$G$ is a linear real algebraic group, then any good 
$G$-space 
$Y$ is a malleable variety. However, it may be the case that 
$Y$ is not rational. This latter fact was communicated to me independently by Olivier Benoist and Olivier Wittenberg.
Theorem 4.3 Let 
$X$, 
$Y$ be nonsingular real algebraic varieties, 
$\mathcal {X}$ a stratification of 
$X$, and 
$k$ a positive integer or 
$k=\infty$. Assume that the variety 
$Y$ is malleable. Then, for a 
$\mathcal {C}^k$ map 
$f \colon X \to Y$, the following conditions are equivalent.
(a)
$f$ can be approximated by $(k,\mathcal {X})$-regular maps.(b)
$f$ is homotopic to a $(k,\mathcal {X})$-regular map.
As recalled in Example 2.6, unit spheres are malleable varieties, so Theorem 4.3 immediately implies the following corollary.
Corollary 4.4 Let 
$X$ be a nonsingular real algebraic variety, 
$\mathcal {X}$ a stratification of 
$X$, 
$p$ a nonnegative integer, and 
$k$ a positive integer or 
$k=\infty$. Then, for a 
$\mathcal {C}^k$ map 
${f \colon X \to \mathbb {S}^p}$, the following conditions are equivalent.
(a)
$f$ can be approximated by $(k,\mathcal {X})$-regular maps.(b)
$f$ is homotopic to a $(k,\mathcal {X})$-regular map.
Next we prove our results on approximation by nice 
$k$-regulous maps announced in § 1.
Proof of Theorem 1.6 (a)
$\,\Rightarrow \,$(b). It is sufficient to prove that any nice 
$k$-regulous map 
$g \colon X \to \mathbb {S}^p$ can be approximated by adapted 
$\mathcal {C}^{\infty }$ maps in the 
$\mathcal {C}^k$ topology. By Sard's theorem, there exists a regular value 
$y \in \mathbb {S}^p \setminus g(P(g))$ for the map 
$g|_{X \setminus P(g)} \colon X \setminus P(g) \to \mathbb {S}^p$. Using partition of unity and radial projection 
$\mathbb {R}^{p+1} \setminus \{0\} \to \mathbb {S}^p$, we readily construct a 
$\mathcal {C}^{\infty }$ map 
$\tilde {g} \colon X \to \mathbb {S}^p$, arbitrarily close to 
$g$ in the 
$\mathcal {C}^k$ topology, such that 
$\tilde {g}^{-1}(y) = g^{-1}(y)$ and 
$\tilde {g} = g$ in a neighborhood of 
$g^{-1}(y)$. By construction, 
$\tilde {g}^{-1}(y)$ is a nonsingular Zariski locally closed subset of 
$X$, so the map 
$\tilde {g}$ is adapted.
(b)
$\,\Rightarrow \,$(a). Our argument is based on Corollary 4.4, so to handle the case 
$k=0$ we choose an integer 
$l > k$. We may assume without loss of generality that the 
$\mathcal {C}^{\infty }$ map 
$f$ is adapted. Let 
$y_0\in \mathbb {S}^p$ be a regular value for 
$f$ such that 
$f^{-1}(y_0)$ is a nonsingular Zariski locally closed subset of 
$X$. By [Reference KucharzKuc09, Theorems 2.4 and 2.5], there exists a nice 
$l$-regulous map 
$\varphi \colon X \to \mathbb {S}^p$, homotopic to 
$f$, such that 
$\varphi ^{-1}(y_0) = f^{-1}(y_0)$ and 
$\varphi (P(\varphi )) \subseteq \{-y_0\}$. Clearly,
\[ f(P(\varphi)) \subset \mathbb{S}^p \setminus \{y_0\}. \]
Using Lemma 2.2(ii), we choose a stratification 
$\mathcal {X}$ of 
$X$ such that 
$X \setminus P(\varphi )$ is a stratum in 
$\mathcal {X}$ and the map 
$\varphi$ is 
$(l,\mathcal {X})$-regular. By Corollary 4.4, 
$f$ can be approximated by 
$(l,\mathcal {X})$-regular maps in the 
$\mathcal {C}^l$ topology. Consequently, 
$f$ can be approximated by 
$(k,\mathcal {X})$-regular maps in the 
$\mathcal {C}^k$ topology. If 
$\tilde f \colon X \to \mathbb {S}^p$ is a 
$(k,\mathcal {X})$-regular map close to 
$f$ in the 
$\mathcal {C}^k$ topology, then 
$\tilde f(P(\varphi )) \subset \mathbb {S}^p \setminus \{y_0\}$. Since 
$P(\tilde f) \subseteq P(\varphi )$, the map 
$\tilde f$ is 
$k$-regulous and nice, hence (a) holds.
(c)
$\,\Rightarrow \,$(b). For the proof we may assume that the map 
$f$ is weakly adapted. Let 
$z_0 \in \mathbb {S}^p$ be a regular value for 
$f$ such that the 
$\mathcal {C}^{\infty }$ submanifold 
$f^{-1}(z_0)$ of 
$X$ admits a weak algebraic approximation. It follows that 
$f^{-1}(z_0)$ is isotopic in 
$X$, via an arbitrarily small 
$\mathcal {C}^{\infty }$ isotopy, to a nonsingular Zariski locally closed subset 
$Z$ of 
$X$. Such an isotopy can be extended to a 
$\mathcal {C}^{\infty }$ ambient isotopy of 
$X$, close to the identity map of 
$X$ in the space 
$\mathcal {C}^{\infty }(X,X)$ (see [Reference HirschHir97, pp. 179, 180]). Thus, there exists a 
$\mathcal {C}^{\infty }$ diffeomorphism 
$\sigma \colon X \to X$ such that 
$\sigma (f^{-1}(z_0)) = Z$ and the composite map 
$f \circ \sigma ^{-1}$ is close to 
$f$ in the 
$\mathcal {C}^k$ topology. By construction, 
$z_0$ is a regular value for the 
$\mathcal {C}^{\infty }$ map 
$f \circ \sigma ^{-1}$, and 
$(f \circ \sigma ^{-1})^{-1}(z_0) = Z$. Consequently, the map 
$f \circ \sigma ^{-1}$ is adapted, as required.
The proof is complete since the implication (b)
$\,\Rightarrow \,$(c) is obvious.
Proof of Theorem 1.9 (d)
$\,\Rightarrow \,$(a). Let 
$M$ be a compact 
$\mathcal {C}^{\infty }$ submanifold of 
$X$, with
\[ 2 \dim M + 1 \leq \dim X, \]
such that the unoriented bordism class of the inclusion map 
$i \colon M \hookrightarrow X$ is algebraic, that is, representable by a regular map from a compact nonsingular real algebraic variety into 
$X$. By Benoist's theorem [Reference BenoistBen20, Theorem 2.7], 
$M$ admits an algebraic approximation in 
$X$, that is, for every neighborhood 
$\mathcal {U}$ of 
$i$ in the space 
$\mathcal {C}^{\infty }(M,X)$ there exists a 
$\mathcal {C}^{\infty }$ embedding 
$e \colon M \to X$ in 
$\mathcal {U}$ such that 
$e(M)$ is a nonsingular Zariski closed subset of 
$X$ (in particular, 
$M$ admits a weak algebraic approximation in 
$X$).
Now suppose that (d) holds. By Sard's theorem, there exists a regular value 
$y\in \mathbb {S}^p$ for 
$f$. It is well known that the 
$\mathbb {Z}/2$-homology class represented by the 
$\mathcal {C}^{\infty }$ submanifold 
$f^{-1}(y)$ of 
$X$ is Poincaré dual to the cohomology class 
$f^*(\sigma _p) \in H^p(X;\mathbb {Z}/2)$ (see [Reference Borel and HaefligerBH61, Proposition 2.15]. Therefore, by [Reference Kucharz and KurdykaKK16, Lemma 2.3], the unoriented bordism class of the inclusion map 
${f^{-1}(y) \hookrightarrow X}$ is algebraic. Consequently, by the Benoist theorem mentioned above, the 
$\mathcal {C}^{\infty }$ submanifold 
$f^{-1}(y)$ admits an algebraic approximation in 
$X$. Thus, the 
$\mathcal {C}^{\infty }$ map 
$f$ is weakly adapted, so, in view of Theorem 1.6, condition (a) holds.
(c)
$\,\Rightarrow \,$(d). Let 
$g \colon X \to \mathbb {S}^p$ be a nice regulous map homotopic to 
$f$. Choose a regular value 
$z \in \mathbb {S}^p \setminus g(P(g))$ of the map 
$g|_{X \setminus P(g)} \colon X \setminus P(g) \to \mathbb {S}^p$. Clearly, the compact 
$\mathcal {C}^{\infty }$ submanifold 
$g^{-1}(z)$ of 
$X$ is a nonsingular Zariski locally closed subset. The 
$\mathbb {Z}/2$-homology class represented by 
$g^{-1}(z)$ is Poincaré dual to the cohomology class 
$g^*(\sigma _p) \in H^p(X; \mathbb {Z}/2)$. We have 
$f^*(\sigma _p) = g^*(\sigma _p)$, the maps 
$f,g$ being homotopic. It follows that the cohomology class 
$f^*(\sigma _p)$ is adapted, and hence (d) holds.
The proof is complete since the implications (a)
$\,\Rightarrow \,$(b) and (b)
$\,\Rightarrow \,$(c) are obvious.
Acknowledgements
The author was partially supported by the National Science Center (Poland) under grant number 2018/31/B/ST1/01059.
Conflicts of Interest
None.
