Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T01:52:19.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Support varieties for rational representations

Part of: Representation theory of groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  13 November 2014

Eric M. Friedlander
Eric M. Friedlander*
Affiliation:
Department of Mathematics, University of Southern California, Los Angeles, CA, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce support varieties for rational representations of a linear algebraic group 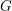$G$ of exponential type over an algebraically closed field 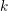$k$ of characteristic 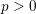$p>0$. These varieties are closed subspaces of the space 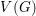$V(G)$ of all 1-parameter subgroups of 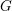$G$. The functor 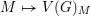$M\mapsto V(G)_{M}$ satisfies many of the standard properties of support varieties satisfied by finite groups and other finite group schemes. Furthermore, there is a close relationship between 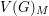$V(G)_{M}$ and the family of support varieties 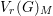$V_{r}(G)_{M}$ obtained by restricting the 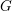$G$ action to Frobenius kernels 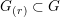$G_{(r)}\subset G$. These support varieties seem particularly appropriate for the investigation of infinite-dimensional rational 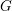$G$-modules.

Keywords

support variety1-parameter subgroup

MSC classification

Primary: 20G05: Representation theory 20C20: Modular representations and characters 20G10: Cohomology theory
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 4 , April 2015 , pp. 765 - 792
Copyright
© The Author 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carlson, J., The varieties and the cohomology ring of a module, J. Algebra 85 (1983), 101–143.Google Scholar
Carlson, J., Lin, Z. and Nakano, D., Support varieties for modules over Chevalley groups and classical Lie algebras, Trans. Amer. Math. Soc. 360 (2008), 1870–1906.Google Scholar
Cline, E., Parshall, B. and Scott, L., Cohomology, hyperalgebras, and representations, J. Algebra 63 (1980), 98–123.Google Scholar
Friedlander, E., Restrictions to G (Fp) and G (r) of rational G-modules, Compositio Math. 147 (2011), 1955–1978.CrossRefGoogle Scholar
Friedlander, E., Spectrum of group cohomology and support varieties, J. K-Theory 11 (2013), 507–516.Google Scholar
Friedlander, E. and Pevtsova, J., Π-supports for modules for finite group schemes, Duke Math. J. 139 (2007), 317–368.CrossRefGoogle Scholar
Friedlander, E. and Pevtsova, J., Generalized support varieties for finite group schemes, Doc. Math. (2010), 197–222.Google Scholar
Friedlander, E. and Pevtsova, J., Constructions for infinitesimal group schemes, Trans. Amer. Math. Soc. 363 (2011), 6007–6061.CrossRefGoogle Scholar
Friedlander, E., Pevtsova, J. and Suslin, A., Generic and Jordan types, Invent. Math. 168 (2007), 485–522.CrossRefGoogle Scholar
Friedlander, E. and Suslin, A., Cohomology of finite group schemes over a field, Invent. Math. 127 (1997), 209–270.Google Scholar
Green, J. A., Polynomial represenations of GLn, Lecture Notes in Mathematics, vol. 830 (Springer, New York, 1980).Google Scholar
Jantzen, J. C., Representations of algebraic groups (Academic Press, New York, 1987).Google Scholar
McNinch, G., Optimal SL(2) homomorphism, Comment. Math. Helv. 80 (2005), 391–426.CrossRefGoogle Scholar
Nakano, D., Parshall, B. J. and Vella, D. C., Support varieties for algebraic groups, J. Reine Angew. Math. 547 (2002), 15–49.Google Scholar
Ostrik, V., Cohomological supports for quantum groups, Funct. Anal. Appl. 32 (1998), 237–246.Google Scholar
Pevtsova, J., Infinite dimensional modules for Frobenius kernels, J. Pure Appl. Algebra 173 (2002), 59–86.Google Scholar
Quillen, D., The spectrum of an equivariant cohomology ring: I, Ann. of Math. (2) 94 (1971), 549–572.CrossRefGoogle Scholar
Quillen, D., The spectrum of an equivariant cohomology ring: II, Ann. of Math. (2) 94 (1971), 573–602.Google Scholar
Seitz, G., Unipotent elements, tilting modules, and saturation, Invent. Math. 141 (2000), 467–502.Google Scholar
Sobaje, P., Support varieties for Frobenius kernels of classical groups, J. Pure Appl. Algebra 216 (2013), 2657–2664.CrossRefGoogle Scholar
Sobaje, P., On exponentiation and infinitesimal one-parameter subgroups of reductive groups, J. Algebra 385 (2013), 14–26.CrossRefGoogle Scholar
Suslin, A., Friedlander, E. and Bendel, C., Infinitesimal 1-parameter subgroups and cohomology, J. Amer. Math. Soc. 10 (1997), 693–728.Google Scholar
Suslin, A., Friedlander, E. and Bendel, C., Support varieties for infinitesimal group schemes, J. Amer. Math. Soc. 10 (1997), 729–759.CrossRefGoogle Scholar