Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Borodin, Alexei
and
Petrov, Leonid
2014.
Integrable probability: From representation theory to Macdonald processes.
Probability Surveys,
Vol. 11,
Issue. none,
Thiery, Thimothée
and
Le Doussal, Pierre
2014.
Log-gamma directed polymer with fixed endpoints via the replica Bethe Ansatz.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2014,
Issue. 10,
p.
P10018.
Borodin, Alexei
Corwin, Ivan
Ferrari, Patrik
and
Vető, Bálint
2015.
Height Fluctuations for the Stationary KPZ Equation.
Mathematical Physics, Analysis and Geometry,
Vol. 18,
Issue. 1,
Spohn, Herbert
and
Sasamoto, Tomohiro
2015.
Point-interacting Brownian motions in the KPZ universality class.
Electronic Journal of Probability,
Vol. 20,
Issue. none,
De Luca, Andrea
and
Le Doussal, Pierre
2015.
Crossing probability for directed polymers in random media.
Physical Review E,
Vol. 92,
Issue. 4,
Ferrari, Patrik L.
and
Vető, Bálint
2015.
Tracy–Widom asymptotics for $q$-TASEP.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 51,
Issue. 4,
Corwin, Ivan
Seppäläinen, Timo
and
Shen, Hao
2015.
The Strict-Weak Lattice Polymer.
Journal of Statistical Physics,
Vol. 160,
Issue. 4,
p.
1027.
Corwin, Ivan
2015.
Theq-Hahn Boson Process andq-Hahn TASEP.
International Mathematics Research Notices,
Vol. 2015,
Issue. 14,
p.
5577.
Ortmann, Janosch
Quastel, Jeremy
and
Remenik, Daniel
2016.
Exact formulas for random growth with half-flat initial data.
The Annals of Applied Probability,
Vol. 26,
Issue. 1,
Borodin, Alexei
Bufetov, Alexey
and
Corwin, Ivan
2016.
Directed random polymers via nested contour integrals.
Annals of Physics,
Vol. 368,
Issue. ,
p.
191.
Borodin, Alexei
2017.
On a family of symmetric rational functions.
Advances in Mathematics,
Vol. 306,
Issue. ,
p.
973.
Orr, Daniel
and
Petrov, Leonid
2017.
Stochastic higher spin six vertex model and q-TASEPs.
Advances in Mathematics,
Vol. 317,
Issue. ,
p.
473.
van Diejen, J. F.
and
Emsiz, E.
2017.
Orthogonality of Bethe Ansatz Eigenfunctions for the Laplacian on a Hyperoctahedral Weyl Alcove.
Communications in Mathematical Physics,
Vol. 350,
Issue. 3,
p.
1017.
Barraquand, Guillaume
and
Corwin, Ivan
2017.
Random-walk in Beta-distributed random environment.
Probability Theory and Related Fields,
Vol. 167,
Issue. 3-4,
p.
1057.
Borodin, Alexei
and
Petrov, Leonid
2018.
Inhomogeneous exponential jump model.
Probability Theory and Related Fields,
Vol. 172,
Issue. 1-2,
p.
323.
Kuan, Jeffrey
2018.
An Algebraic Construction of Duality Functions for the Stochastic $${\mathcal{U}_q( A_n^{(1)})}$$ Vertex Model and Its Degenerations.
Communications in Mathematical Physics,
Vol. 359,
Issue. 1,
p.
121.
van Diejen, Jan Felipe
Emsiz, Erdal
and
Zurrián, Ignacio Nahuel
2018.
Completeness of the Bethe Ansatz for an Open $$\varvec{q}$$ q -Boson System with Integrable Boundary Interactions.
Annales Henri Poincaré,
Vol. 19,
Issue. 5,
p.
1349.
BUFETOV, ALEXEY
and
PETROV, LEONID
2019.
YANG–BAXTER FIELD FOR SPIN HALL–LITTLEWOOD SYMMETRIC FUNCTIONS.
Forum of Mathematics, Sigma,
Vol. 7,
Issue. ,
Franceschini, Chiara
and
Giardinà, Cristian
2019.
Sojourns in Probability Theory and Statistical Physics - III.
Vol. 300,
Issue. ,
p.
187.
Lee, Eunghyun
and
Wang, Dong
2019.
Distributions of a particle’s position and their asymptotics in the q-deformed totally asymmetric zero range process with site dependent jumping rates.
Stochastic Processes and their Applications,
Vol. 129,
Issue. 5,
p.
1795.
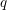 $q$-Boson particle system
$q$-Boson particle system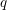 $q$-Boson (stochastic) particle system. Our central result is a Plancherel type isomorphism theorem for this system. This theorem has various implications. It proves the completeness of the Bethe ansatz for the
$q$-Boson (stochastic) particle system. Our central result is a Plancherel type isomorphism theorem for this system. This theorem has various implications. It proves the completeness of the Bethe ansatz for the 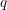 $q$-Boson generator and consequently enables us to solve the Kolmogorov forward and backward equations for general initial data. Owing to a Markov duality with
$q$-Boson generator and consequently enables us to solve the Kolmogorov forward and backward equations for general initial data. Owing to a Markov duality with 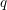 $q$-TASEP (
$q$-TASEP (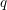 $q$-deformed totally asymmetric simple exclusion process), this leads to moment formulas which characterize the fixed time distribution of
$q$-deformed totally asymmetric simple exclusion process), this leads to moment formulas which characterize the fixed time distribution of 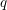 $q$-TASEP started from general initial conditions. The theorem also implies the biorthogonality of the left and right eigenfunctions. We consider limits of our
$q$-TASEP started from general initial conditions. The theorem also implies the biorthogonality of the left and right eigenfunctions. We consider limits of our 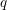 $q$-Boson results to a discrete delta Bose gas considered previously by van Diejen, as well as to another discrete delta Bose gas that describes the evolution of moments of the semi-discrete stochastic heat equation (or equivalently, the O’Connell–Yor semi-discrete directed polymer partition function). A further limit takes us to the delta Bose gas which arises in studying moments of the stochastic heat equation/Kardar–Parisi–Zhang equation.
$q$-Boson results to a discrete delta Bose gas considered previously by van Diejen, as well as to another discrete delta Bose gas that describes the evolution of moments of the semi-discrete stochastic heat equation (or equivalently, the O’Connell–Yor semi-discrete directed polymer partition function). A further limit takes us to the delta Bose gas which arises in studying moments of the stochastic heat equation/Kardar–Parisi–Zhang equation.

