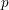Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T16:24:19.084Z Has data issue: false hasContentIssue false
  • English
  • Français

On the complexity of a putative counterexample to the $p$-adic Littlewood conjecture

Part of: Diophantine approximation, transcendental number theory Dynamical systems with hyperbolic behavior Ergodic theory

Published online by Cambridge University Press:  19 May 2015

Dmitry Badziahin ,
Yann Bugeaud ,
Manfred Einsiedler  and
Dmitry Kleinbock
Dmitry Badziahin
Affiliation:
University of Durham, Department of Mathematical Sciences, South Rd, Durham DH1 3LE, UK email [email protected]
Yann Bugeaud
Affiliation:
Université de Strasbourg, Mathématiques, 7 rue René Descartes, 67084 Strasbourg Cedex, France email [email protected]
Manfred Einsiedler
Affiliation:
ETH Zürich, Departement Mathematik, Rämistrasse 101, CH-8092 Zürich, Switzerland email [email protected]
Dmitry Kleinbock
Affiliation:
Brandeis University, Department of Mathematics, Waltham, MA 02454, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

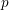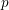Let $\Vert \cdot \Vert$ denote the distance to the nearest integer and, for a prime number $p$, let $|\cdot |_{p}$ denote the $p$-adic absolute value. Over a decade ago, de Mathan and Teulié [Problèmes diophantiens simultanés, Monatsh. Math. 143 (2004), 229–245] asked whether 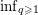$\inf _{q\geqslant 1}$$q\cdot \Vert q{\it\alpha}\Vert \cdot |q|_{p}=0$ holds for every badly approximable real number 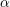${\it\alpha}$ and every prime number 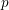$p$. Among other results, we establish that, if the complexity of the sequence of partial quotients of a real number 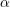${\it\alpha}$ grows too rapidly or too slowly, then their conjecture is true for the pair 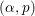$({\it\alpha},p)$ with 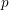$p$ an arbitrary prime.

Keywords

Diophantine approximationLittlewood conjecturecomplexitycontinued fractionsmeasure rigidity

MSC classification

Primary: 11J04: Homogeneous approximation to one number
Secondary: 11J61: Approximation in non-Archimedean valuations 11J83: Metric theory 37A35: Entropy and other invariants, isomorphism, classification 37A45: Relations with number theory and harmonic analysis 37D40: Dynamical systems of geometric origin and hyperbolicity (geodesic and horocycle flows, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 9 , September 2015 , pp. 1647 - 1662
Copyright
© The Authors 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Allouche, J.-P. and Shallit, J., Automatic sequences: theory, applications, generalizations (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Badziahin, D. and Velani, S., Multiplicatively badly approximable numbers and the mixed Littlewood conjecture, Adv. Math. 228 (2011), 2766–2796.CrossRefGoogle Scholar
Bugeaud, Y., Approximation by algebraic numbers, Cambridge Tracts in Mathematics, vol. 160 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Bugeaud, Y., Around the Littlewood conjecture in diophantine approximation, Publ. Math. Besançon Algèbr. Théor. Nr. (1) (2014), 5–18.Google Scholar
Bugeaud, Y., Drmota, M. and de Mathan, B., On a mixed Littlewood conjecture in Diophantine approximation, Acta Arith. 128 (2007), 107–124.CrossRefGoogle Scholar
Cassaigne, J., Sequences with grouped factors, in Proceedings of the third international conference. Developments in language theory, ed. Bozapalidis, S. (Aristotle University of Thessaloniki, 1997), 211–222.Google Scholar
Cassels, J. W. S. and Swinnerton-Dyer, H. P. F., On the product of three homogeneous linear forms and indefinite ternary quadratic forms, Philos. Trans. R. Soc. Lond. A 248 (1955), 73–96.Google Scholar
de Mathan, B. and Teulié, O., Problèmes diophantiens simultanés, Monatsh. Math. 143 (2004), 229–245.CrossRefGoogle Scholar
Einsiedler, M., Fishman, L. and Shapira, U., Diophantine approximation on fractals, Geom. Funct. Anal. 21 (2011), 14–35.CrossRefGoogle Scholar
Einsiedler, M., Katok, A. and Lindenstrauss, E., Invariant measures and the set of exceptions to the Littlewood conjecture, Ann. of Math. (2) 164 (2006), 513–560.CrossRefGoogle Scholar
Einsiedler, M. and Kleinbock, D., Measure rigidity and p-adic Littlewood-type problems, Compositio Math. 143 (2007), 689–702.CrossRefGoogle Scholar
Einsiedler, M. and Lindenstrauss, E., On measures invariant under tori on quotients of semisimple groups, Ann. of Math. (2) 181 (2015), 993–1031.CrossRefGoogle Scholar
Everest, G., van der Poorten, A., Shparlinski, I. and Ward, T., Recurrence sequences, Mathematical Surveys and Monographs, vol. 104 (American Mathematical Society, Providence, RI, 2003).CrossRefGoogle Scholar
Lenstra, H. W. and Shallit, J. O., Continued fractions and linear recurrences, Math. Comp. 61 (1993), 351–354.CrossRefGoogle Scholar
Lindenstrauss, E., Invariant measures and arithmetic quantum unique ergodicity, Ann. of Math. (2) 163 (2006), 165–219.CrossRefGoogle Scholar
Lindenstrauss, E., Equidistribution in homogeneous spaces and number theory, in Proceedings of the International Congress of Mathematicians, Vol. I (Hindustan Book Agency, New Delhi, 2010), 531–557.Google Scholar
Morse, M. and Hedlund, G. A., Symbolic dynamics, Amer. J. Math. 60 (1938), 815–866.CrossRefGoogle Scholar
Morse, M. and Hedlund, G. A., Symbolic dynamics II, Amer. J. Math. 62 (1940), 1–42.CrossRefGoogle Scholar
Perron, O., Die Lehre von den Ketterbrüchen (Teubner, Leipzig, 1929).Google Scholar
Pollington, A. D. and Velani, S., On a problem in simultaneous Diophantine approximation: Littlewood’s conjecture, Acta Math. 185 (2000), 287–306.CrossRefGoogle Scholar