Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T13:48:58.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective limit distribution of the Frobenius numbers

Part of: Geometry of numbers Probabilistic theory: distribution modulo $1$; metric theory of algorithms Diophantine equations Ergodic theory Sequences and sets

Published online by Cambridge University Press:  22 December 2014

Han Li
Han Li*
Affiliation:
Department of Mathematics, Yale University, New Haven, CT 06520, USA email [email protected] Current address: Department of Mathematics, The University of Texas at Austin, Austin, TX 78750, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

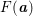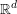The Frobenius number $F(\boldsymbol{a})$ of a lattice point $\boldsymbol{a}$ in $\mathbb{R}^{d}$ with positive coprime coordinates, is the largest integer which can not be expressed as a non-negative integer linear combination of the coordinates of $\boldsymbol{a}$. Marklof in [The asymptotic distribution of Frobenius numbers, Invent. Math. 181 (2010), 179–207] proved the existence of the limit distribution of the Frobenius numbers, when $\boldsymbol{a}$ is taken to be random in an enlarging domain in 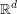$\mathbb{R}^{d}$. We will show that if the domain has piecewise smooth boundary, the error term for the convergence of the distribution function is at most a polynomial in the enlarging factor.

Keywords

Frobenius numbersFarey fractionshomogeneous dynamicseffective equidistribution

MSC classification

Primary: 37A25: Ergodicity, mixing, rates of mixing 11K31: Special sequences
Secondary: 11B57: Farey sequences; the sequences ${1^k, 2^k, cdots}$ 11D07: The Frobenius problem 11H06: Lattices and convex bodies
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 5 , May 2015 , pp. 898 - 916
Copyright
© The Author 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliev, I. M. and Gruber, P. M., An optimal lower bound for the Frobenius problem, J. Number Theory 123 (2007), 71–79.CrossRefGoogle Scholar
Aliev, I. M., Henk, M. and Hinrichs, A., Expected Frobenius numbers, J. Combin. Theory Ser. A 118 (2011), 525–531.CrossRefGoogle Scholar
Athreya, J. S. and Margulis, G. A., Logarithm laws for unipotent flows, I, J. Mod. Dyn. 3 (2009), 359–378.CrossRefGoogle Scholar
Bochnak, J., Coste, M. and Roy, M.-F., Real algebraic geometry (Springer, 1998).CrossRefGoogle Scholar
Bourgain, J. and Sinai, Ya. G., Limit behavior of large Frobenius numbers, Russian Math. Surveys 62 (2007), 713–725.CrossRefGoogle Scholar
Cowling, M., Sur le coefficients des représentations unitaries des groupes de Lie simple, Lecture Notes in Mathematics, vol. 739 (Springer, New York, 1979), 132–178.Google Scholar
Erdős, P. and Graham, R., On a linear Diophantine problem of Frobenius, Acta Arith. 21 (1972), 399–408.CrossRefGoogle Scholar
Howe, R., On a notion of rank for unitary representations of the classical groups, in Harmonic analysis and group representations (Liguori, Naples, 1982), 223–331.Google Scholar
Kannan, R., Lattice translates of a polytope and the Frobenius problem, Combinatorica 12 (1992), 161–177.CrossRefGoogle Scholar
Kannan, R. and Lovász, L., Covering minima and lattice-point-free convex bodies, Ann. of Math. (2) 128 (1988), 577–602.CrossRefGoogle Scholar
Katok, A. and Spatzier, R., First cohomology of Anosov actions of higher rank Abelian groups and applications to rigidity, Publ. Math. Inst. Hautes Études Sci. 79 (1994), 131–156.CrossRefGoogle Scholar
Kleinbock, D. and Margulis, G. A., Bounded orbits of nonquasiunipotent flows on homogeneous spaces, Amer. Math. Soc. Transl. 171 (1996), 141–172.Google Scholar
Kleinbock, D. and Margulis, G. A., On effective equidistribution of expanding translates of certain orbits in the space of lattices, in Number theory, analysis and geometry (Springer, New York, 2012), 385–396.CrossRefGoogle Scholar
Knapp, A., Lie groups beyond an introduction (Birkhäuser, Boston, 2002).Google Scholar
Marklof, J., The asymptotic distribution of Frobenius numbers, Invent. Math. 181 (2010), 179–207.CrossRefGoogle Scholar
Moore, C. C., Exponential decay of correlation coefficients for geodesic flows, in Group representations, ergodic theory, operator algebras, and mathematical physics (Berkeley, California, 1984), Mathematical Sciences Research Institute Publications (Springer, New York, 1987), 163–181.CrossRefGoogle Scholar
Oh, H., Uniform pointwise bounds for matrix coefficients of unitary representations and applications to Kazhdan constants, Duke Math. J. 113 (2002), 133–192.CrossRefGoogle Scholar
Ramirez Alfonsin, J., The diophantine Frobenius problem (Oxford University Press, 2005).CrossRefGoogle Scholar
Selmer, E., On the linear Diophantine problem of Frobenius, J. Reine Angew. Math. 293/294 (1977), 1–17.Google Scholar
Siegel, C. L., A mean value theorem in geometry of numbers, Ann. of Math. (2) 46 (1945), 340–347.CrossRefGoogle Scholar
Strömbergsson, A., On the limit distribution of Frobenius numbers, Acta Arith. 152 (2012), 81–107.CrossRefGoogle Scholar
Strömbergsson, A. and Venkatesh, A., Small solutions to linear congruences and Hecke equidistribution, Acta Arith. 118 (2005), 41–78.CrossRefGoogle Scholar
Ustinov, A., On the distribution of Frobenius numbers with three arguments, Izv. RAN. Ser. Mat. 74 (2010), 145–170.Google Scholar