Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T01:39:38.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute Hodge and ℓ-adic monodromy

Part of: Cycles and subschemes Families, fibrations Deformations of analytic structures

Published online by Cambridge University Press:  13 May 2022

David Urbanik
David Urbanik*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Canada [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 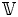$\mathbb {V}$ be a motivic variation of Hodge structure on a 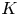$K$-variety 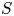$S$, let 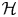$\mathcal {H}$ be the associated 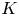$K$-algebraic Hodge bundle, and let 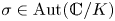$\sigma \in \mathrm {Aut}(\mathbb {C}/K)$ be an automorphism. The absolute Hodge conjecture predicts that given a Hodge vector 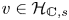$v \in \mathcal {H}_{\mathbb {C}, s}$ above 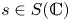$s \in S(\mathbb {C})$ which lies inside 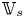$\mathbb {V}_{s}$, the conjugate vector 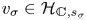$v_{\sigma } \in \mathcal {H}_{\mathbb {C}, s_{\sigma }}$ is Hodge and lies inside 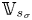$\mathbb {V}_{s_{\sigma }}$. We study this problem in the situation where we have an algebraic subvariety 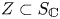$Z \subset S_{\mathbb {C}}$ containing 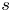$s$ whose algebraic monodromy group 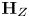$\textbf {H}_{Z}$ fixes $v$. Using relationships between 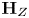$\textbf {H}_{Z}$ and 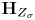$\textbf {H}_{Z_{\sigma }}$ coming from the theories of complex and 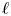$\ell$-adic local systems, we establish a criterion that implies the absolute Hodge conjecture for 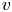$v$ subject to a group-theoretic condition on 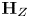$\textbf {H}_{Z}$. We then use our criterion to establish new cases of the absolute Hodge conjecture.

Keywords

Hodge theoryabsolute Hodge classesℓ-adic monodromy

MSC classification

Primary: 14D07: Variation of Hodge structures
Secondary: 32G20: Period matrices, variation of Hodge structure; degenerations 14C25: Algebraic cycles
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 3 , March 2022 , pp. 568 - 584
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bakker, B., Brunebarbe, Y. and Tsimerman, J., o-minimal GAGA and a conjecture of Griffiths, Preprint (2018), arXiv:1811.12230.Google Scholar
Carlson, J. A., Peters, C. and Müller-Stach, S., Period mappings and period domains (Cambridge University Press, Cambridge, 2003).Google Scholar
Cassels, J. W. S. and Frölich, A., Algebraic number theory: proceedings of an instructional conference (Academic Press, London, 1967).Google Scholar
Charles, F. and Schnell, C., Notes on absolute Hodge classes, in Hodge theory (Princeton University Press, Princeton, NJ, 2014), 469–530.CrossRefGoogle Scholar
Conrad, B., Étale cohomology, available at http://math.stanford.edu/~conrad/Weil2seminar/Notes/etnotes.pdf.Google Scholar
Deligne, P., Théorie de Hodge: II, Publ. Math. Inst. Hautes Études Sci. 40 (1971), 5–57.10.1007/BF02684692CrossRefGoogle Scholar
Deligne, P., Hodge cycles on Abelian varieties (Springer, Berlin, 1982), 9–100.CrossRefGoogle Scholar
Deligne, P., Hodge cycles on Abelian varieties (notes by J. Milne), in Hodge cycles, motives, and Shimura varieties, Lecture Notes in Mathematics, vol. 900 (Springer, Berlin, 1982).CrossRefGoogle Scholar
Hartshorne, R., On the de Rham cohomology of algebraic varieties, Publ. Math. Inst. Hautes Études Sci. 45 (1975), 6–99.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry (Springer, New York, 1977).CrossRefGoogle Scholar
Katz, N. M. and Oda, T., On the differentiation of De Rham cohomology classes with respect to parameters, J. Math. Kyoto Univ. 8 (1968), 199–213.Google Scholar
Klingler, B., Otwinowska, A. and Urbanik, D., On the fields of definition of Hodge loci, Ann. Sci. Éc. Norm. Supér. (4), to appear. Preprint (2020), arXiv:2010.03359.Google Scholar
Kollár, J., Fundamental groups and path lifting for algebraic varieties, Preprint (2019), arXiv:1906.11816.Google Scholar
Milne, J. S., Etale cohomology (PMS-33) (Princeton University Press, Princeton, NJ, 1980).CrossRefGoogle Scholar
The Stacks Project Authors, The Stacks Project (2020), https://stacks.math.columbia.edu.Google Scholar
Voisin, C., Hodge theory and complex algebraic geometry II, Cambridge Studies in Advanced Mathematics, vol. 2 (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Voisin, C., Hodge loci and absolute Hodge classes, Compos. Math. 143 (2007), 945–958.10.1112/S0010437X07002837CrossRefGoogle Scholar