Research Article
A Winning Strategy for the Ramsey Graph Game
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 267-276
-
- Article
- Export citation
Topological cliques in graphs II
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 79-90
-
- Article
- Export citation
Subset sums in ℕ2
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 393-402
-
- Article
- Export citation
A Phase Transition for the Distribution of Matching Blocks
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 139-159
-
- Article
- Export citation
Paths, Stars and the Number Three
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 277-295
-
- Article
- Export citation
An Efficient Method of Examining all Trees
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 403-413
-
- Article
- Export citation
Short Proof of Galvin's Theorem on the List-chromatic Index of a Bipartite Multigraph
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 91-94
-
- Article
- Export citation
Computing Norms of Group-Invariant Transition Operators
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 161-178
-
- Article
- Export citation
Fast String Matching in Stationary Ergodic Sources
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 415-427
-
- Article
- Export citation
K5-Subdivisions in Graphs
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 179-189
-
- Article
- Export citation
Front matter
CPC volume 5 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Finding a Longest Alternating Cycle in a 2-edge-coloured Complete Graph is in RP
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 297-306
-
- Article
- Export citation
Back matter
CPC volume 5 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Research Article
Smallest Sets of Longest Paths with Empty Intersection
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 429-436
-
- Article
- Export citation
Front matter
CPC volume 5 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
On Recognition of Shift Registers
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 307-315
-
- Article
- Export citation
Front matter
CPC volume 5 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
CPC volume 5 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Research Article
On the Number of Hamiltonian Cycles in Bipartite Graphs
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 437-442
-
- Article
- Export citation
Back matter
CPC volume 5 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b5
-
- Article
-
- You have access
- Export citation

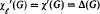 . Here we give a brief self-contained proof of this result.
. Here we give a brief self-contained proof of this result.