Paper
Playing to Retain the Advantage
-
- Published online by Cambridge University Press:
- 19 March 2010, pp. 481-491
-
- Article
- Export citation
Online Conflict-Free Colouring for Hypergraphs
-
- Published online by Cambridge University Press:
- 11 December 2009, pp. 493-516
-
- Article
- Export citation
What Does a Random Contingency Table Look Like?
-
- Published online by Cambridge University Press:
- 12 February 2010, pp. 517-539
-
- Article
- Export citation
Exit Frequency Matrices for Finite Markov Chains
-
- Published online by Cambridge University Press:
- 14 May 2010, pp. 541-560
-
- Article
-
- You have access
- Export citation
On the Subtree Size Profile of Binary Search trees
-
- Published online by Cambridge University Press:
- 22 January 2010, pp. 561-578
-
- Article
- Export citation
Vertex-Bipartition Method for Colouring Minor-Closed Classes of Graphs
-
- Published online by Cambridge University Press:
- 21 April 2010, pp. 579-591
-
- Article
- Export citation
First-Passage Percolation with Exponential Times on a Ladder
-
- Published online by Cambridge University Press:
- 19 March 2010, pp. 593-601
-
- Article
- Export citation
Sumset and Inverse Sumset Theory for Shannon Entropy
-
- Published online by Cambridge University Press:
- 22 January 2010, pp. 603-639
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 19 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 28 May 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 19 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 28 May 2010, pp. b1-b3
-
- Article
-
- You have access
- Export citation


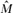
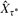 denote the matrix of exit frequencies from singletons to τ* on the reverse chain. We show that
denote the matrix of exit frequencies from singletons to τ* on the reverse chain. We show that 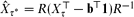 , where
, where 
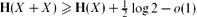 , where
, where