Article contents
Exit Frequency Matrices for Finite Markov Chains
Published online by Cambridge University Press: 14 May 2010
Abstract
Consider a finite irreducible Markov chain on state space S with transition matrix M and stationary distribution π. Let R be the diagonal matrix of return times, Rii = 1/πi. Given distributions σ, τ and k ∈ S, the exit frequency xk(σ, τ) denotes the expected number of times a random walk exits state k before an optimal stopping rule from σ to τ halts the walk. For a target distribution τ, we define Xτ as the n × n matrix given by (Xτ)ij = xj(i, τ), where i also denotes the singleton distribution on state i.
The dual Markov chain with transition matrix 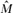 = RM⊤R−1 is called the reverse chain. We prove that Markov chain duality extends to matrices of exit frequencies. Specifically, for each target distribution τ, we associate a unique dual distribution τ*. Let
= RM⊤R−1 is called the reverse chain. We prove that Markov chain duality extends to matrices of exit frequencies. Specifically, for each target distribution τ, we associate a unique dual distribution τ*. Let 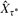 denote the matrix of exit frequencies from singletons to τ* on the reverse chain. We show that
denote the matrix of exit frequencies from singletons to τ* on the reverse chain. We show that 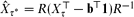 , where b is a non-negative constant vector (depending on τ). We explore this exit frequency duality and further illuminate the relationship between stopping rules on the original chain and reverse chain.
, where b is a non-negative constant vector (depending on τ). We explore this exit frequency duality and further illuminate the relationship between stopping rules on the original chain and reverse chain.
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2010
References
- 2
- Cited by


