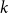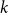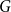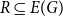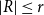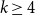1. Introduction
The chromatic number
![]() $\chi (G)$
of a graph
$\chi (G)$
of a graph
![]() $G$
is among the oldest and most fundamental graph parameters, but despite its intensive study by researchers across the field for more than a century, many fundamental open problems remain. In many instances, we would like to show that for some number
$G$
is among the oldest and most fundamental graph parameters, but despite its intensive study by researchers across the field for more than a century, many fundamental open problems remain. In many instances, we would like to show that for some number
![]() $k$
, all graphs in an infinite class
$k$
, all graphs in an infinite class
![]() $\mathcal{G}$
of graphs have chromatic number less than
$\mathcal{G}$
of graphs have chromatic number less than
![]() $k$
. Often times, the graph class
$k$
. Often times, the graph class
![]() $\mathcal{G}$
at hand will also have the property that it is closed under taking induced, or even arbitrary, subgraphs. In this case, a central idea for bounding the chromatic number is to consider the minimal graphs in
$\mathcal{G}$
at hand will also have the property that it is closed under taking induced, or even arbitrary, subgraphs. In this case, a central idea for bounding the chromatic number is to consider the minimal graphs in
![]() $\mathcal{G}$
with chromatic number
$\mathcal{G}$
with chromatic number
![]() $k$
. These graphs have the special property that removing any vertex (if
$k$
. These graphs have the special property that removing any vertex (if
![]() $\mathcal{G}$
is closed under induced subgraphs) or any edge (if
$\mathcal{G}$
is closed under induced subgraphs) or any edge (if
![]() $G$
is closed under subgraphs) reduces the chromatic number from
$G$
is closed under subgraphs) reduces the chromatic number from
![]() $k$
to
$k$
to
![]() $k-1$
. This enforces many constraints on such minimal graphs, for instance sufficiently high minimum degree and edge-connectivity, among others. Such properties can then prove useful when showing the non-existence of minimal
$k-1$
. This enforces many constraints on such minimal graphs, for instance sufficiently high minimum degree and edge-connectivity, among others. Such properties can then prove useful when showing the non-existence of minimal
![]() $k$
-chromatic graphs in
$k$
-chromatic graphs in
![]() $\mathcal{G}$
, which in turn establishes that the chromatic number of graphs in
$\mathcal{G}$
, which in turn establishes that the chromatic number of graphs in
![]() $\mathcal{G}$
is less than
$\mathcal{G}$
is less than
![]() $k$
.
$k$
.
Because of this and many other applications, the notion of colour-critical graphs has emerged. Given an integer
![]() $k$
, a graph
$k$
, a graph
![]() $G$
is called
$G$
is called
![]() $k$
-chromatic vertex-critical if
$k$
-chromatic vertex-critical if
![]() $\chi (G)=k$
, but
$\chi (G)=k$
, but
![]() $\chi (G-v)=k-1$
for every
$\chi (G-v)=k-1$
for every
![]() $v \in V(G)$
. Similarly, it is called
$v \in V(G)$
. Similarly, it is called
![]() $k$
-chromatic edge-critical, if
$k$
-chromatic edge-critical, if
![]() $\chi (G)=k$
but
$\chi (G)=k$
but
![]() $\chi (G-e)=k$
for every
$\chi (G-e)=k$
for every
![]() $e \in E(G)$
. Note that edge-criticality implies vertex-criticality if we exclude redundant cases in which
$e \in E(G)$
. Note that edge-criticality implies vertex-criticality if we exclude redundant cases in which
![]() $G$
has isolated vertices.
$G$
has isolated vertices.
A considerable amount of effort has been put into understanding how different the notions of vertex-criticality and edge-criticality can be. Already in 1970, G. Dirac [Reference Lattanzio5] conjectured that for every integer
![]() $k \ge 4$
, there exists a
$k \ge 4$
, there exists a
![]() $k$
-chromatic vertex-critical graph
$k$
-chromatic vertex-critical graph
![]() $G$
which at the same time is very much not edge-critical, in the sense that the deletion of any single edge does not lower its chromatic number. In the following, let us say that such a graph has no critical edges. Dirac’s problem for a long time remained poorly understood. It was not before 1992 that Brown [Reference Brown1] finally found a first construction of some vertex-critical graph with no critical edges, in fact, he found such a construction for
$G$
which at the same time is very much not edge-critical, in the sense that the deletion of any single edge does not lower its chromatic number. In the following, let us say that such a graph has no critical edges. Dirac’s problem for a long time remained poorly understood. It was not before 1992 that Brown [Reference Brown1] finally found a first construction of some vertex-critical graph with no critical edges, in fact, he found such a construction for
![]() $k=5$
. Later, in 2002, Lattanzio [Reference Lattanzio5] found a more general construction which proved Dirac’s conjecture for every integer
$k=5$
. Later, in 2002, Lattanzio [Reference Lattanzio5] found a more general construction which proved Dirac’s conjecture for every integer
![]() $k \ge 5$
such that
$k \ge 5$
such that
![]() $k-1$
is not a prime number. Shortly after, Jensen [Reference Jensen6] provided a construction of
$k-1$
is not a prime number. Shortly after, Jensen [Reference Jensen6] provided a construction of
![]() $k$
-chromatic vertex-critical graphs with no critical edges for every
$k$
-chromatic vertex-critical graphs with no critical edges for every
![]() $k \ge 5$
. This leaves only the case
$k \ge 5$
. This leaves only the case
![]() $k=4$
of Dirac’s conjecture open today, which remains an intriguing open problem. A wide-ranging strengthening of Dirac’s conjecture was proposed by Erdős in 1985 [Reference Erdős, Andersen and Jakobsen4], as follows.
$k=4$
of Dirac’s conjecture open today, which remains an intriguing open problem. A wide-ranging strengthening of Dirac’s conjecture was proposed by Erdős in 1985 [Reference Erdős, Andersen and Jakobsen4], as follows.
‘I recently heard from Toft the following conjecture of Dirac: Is it true that for every
![]() $k \ge 4$
there is a
$k \ge 4$
there is a
![]() $k$
-chromatic vertex-critical graph which remains
$k$
-chromatic vertex-critical graph which remains
![]() $k$
-chromatic if any of its edges is omitted. If the answer as expected is yes, then one could ask whether it is true that for every
$k$
-chromatic if any of its edges is omitted. If the answer as expected is yes, then one could ask whether it is true that for every
![]() $k \ge 4$
and
$k \ge 4$
and
![]() $r$
there is a vertex-critical
$r$
there is a vertex-critical
![]() $k$
-chromatic graph which remains
$k$
-chromatic graph which remains
![]() $k$
-chromatic if any
$k$
-chromatic if any
![]() $r$
of its edges are omitted’.
$r$
of its edges are omitted’.
(Paul Erdős, 1985, top of page 113 in [Reference Erdős, Andersen and Jakobsen4])
This problem is also mentioned in several other sources, for instance it is listed as Problem 5.14 in the book [Reference Jensen, Toft, Graham, Lenstra and Tarjan8] by Jensen and Toft and on page 66 in Chapter 4 of the Erdős open problem collection by Chung and Graham [Reference Chung and Graham2], see also the online version of the problem [Reference Chung3].
The question of Erdős can be rephrased as asking whether for arbitrarily large numbers
![]() $r$
there exist
$r$
there exist
![]() $k$
-chromatic vertex-critical graphs for
$k$
-chromatic vertex-critical graphs for
![]() $k \ge 4$
that are ‘pretty far’ from any of their
$k \ge 4$
that are ‘pretty far’ from any of their
![]() $(k-1)$
-chromatic spanning subgraphs, in the sense that one has to remove more than
$(k-1)$
-chromatic spanning subgraphs, in the sense that one has to remove more than
![]() $r$
edges to reach any such subgraph. As described above, the case
$r$
edges to reach any such subgraph. As described above, the case
![]() $r=1$
of this problem is well-understood, however, not much seems to be known beyond that, when
$r=1$
of this problem is well-understood, however, not much seems to be known beyond that, when
![]() $r\ge 2$
.
$r\ge 2$
.
Our contribution. In this paper, we resolve the problem by Erdős for any value
![]() $r$
and all sufficiently large values
$r$
and all sufficiently large values
![]() $k$
. To the best of our knowledge, these are the first known examples of such graphs for arbitrarily large values of
$k$
. To the best of our knowledge, these are the first known examples of such graphs for arbitrarily large values of
![]() $r$
.
$r$
.
Theorem 1.1.
For every
![]() $r \in \mathbb{N}$
there is some
$r \in \mathbb{N}$
there is some
![]() $k_0\in \mathbb{N}$
such that for every
$k_0\in \mathbb{N}$
such that for every
![]() $k \ge k_0$
there exists a
$k \ge k_0$
there exists a
![]() $k$
-chromatic vertex-critical graph
$k$
-chromatic vertex-critical graph
![]() $G$
such that
$G$
such that
![]() $\chi (G-R)=k$
for every
$\chi (G-R)=k$
for every
![]() $R \subseteq E(G)$
with
$R \subseteq E(G)$
with
![]() $|R|\le r$
.
$|R|\le r$
.
We remark that the graphs in Theorem1.1 have the additional feature that also their fractional chromatic number
![]() $\chi _f(G)$
is large (in fact, bigger than
$\chi _f(G)$
is large (in fact, bigger than
![]() $k-1$
), which may be useful to know in some applications.
$k-1$
), which may be useful to know in some applications.
Our result still leaves open Erdős’ question when
![]() $k\ge 4$
is fixed as a small value and
$k\ge 4$
is fixed as a small value and
![]() $r$
tends to infinity, and this remains an interesting open case of the problem. The rest of this note is devoted to presenting our proof of Theorem1.1. The main idea of the construction is to use the existence of uniform hypergraphs that admit a perfect matching upon the removal of any single vertex, but at the same time are locally rather sparse. Such hypergraphs in turn can be constructed randomly, using the recent advances on Shamir’s hypergraph matching problem.
$r$
tends to infinity, and this remains an interesting open case of the problem. The rest of this note is devoted to presenting our proof of Theorem1.1. The main idea of the construction is to use the existence of uniform hypergraphs that admit a perfect matching upon the removal of any single vertex, but at the same time are locally rather sparse. Such hypergraphs in turn can be constructed randomly, using the recent advances on Shamir’s hypergraph matching problem.
Notation. For a graph
![]() $G$
and a subset
$G$
and a subset
![]() $X\subseteq V(G)$
of its vertices,
$X\subseteq V(G)$
of its vertices,
![]() $G[X]$
denotes the subgraph of
$G[X]$
denotes the subgraph of
![]() $G$
induced by
$G$
induced by
![]() $X$
. A hypergraph is a tuple
$X$
. A hypergraph is a tuple
![]() $(V,E)$
where
$(V,E)$
where
![]() $V$
is a finite set and
$V$
is a finite set and
![]() $E \subseteq 2^V\setminus \{\emptyset \}$
. Given a hypergraph
$E \subseteq 2^V\setminus \{\emptyset \}$
. Given a hypergraph
![]() $H=(V,E)$
, we denote by
$H=(V,E)$
, we denote by
![]() $V(H)=V$
its vertex- and by
$V(H)=V$
its vertex- and by
![]() $E(H)=E$
its hyperedge-set. For
$E(H)=E$
its hyperedge-set. For
![]() $v \in V(H)$
, we denote by
$v \in V(H)$
, we denote by
![]() $H-v$
the hypergraph with vertex-set
$H-v$
the hypergraph with vertex-set
![]() $V(H)\setminus \{v\}$
and hyperedge-set
$V(H)\setminus \{v\}$
and hyperedge-set
![]() $\{e\in E(H)|v \notin e\}$
. For
$\{e\in E(H)|v \notin e\}$
. For
![]() $e \in E(H)$
,
$e \in E(H)$
,
![]() $H-e\, :\!= (V(H),E(H)\setminus \{e\})$
is the hypergraph obtained by omitting
$H-e\, :\!= (V(H),E(H)\setminus \{e\})$
is the hypergraph obtained by omitting
![]() $e$
. For a vertex subset
$e$
. For a vertex subset
![]() $X\subseteq V$
, we denote by
$X\subseteq V$
, we denote by
![]() $H_X$
the hypergraph obtained by restricting
$H_X$
the hypergraph obtained by restricting
![]() $H$
to
$H$
to
![]() $X$
, i.e.,
$X$
, i.e.,
![]() $V(H_X)\, :\!= X$
and
$V(H_X)\, :\!= X$
and
![]() $E(H_X)=\{e \cap X|e \in E(H), |e\cap X|\ge 2\}$
.
$E(H_X)=\{e \cap X|e \in E(H), |e\cap X|\ge 2\}$
.
2. Proof of Theorem1.1
Outline. In order to ease the reader’s orientation, we give a brief outline of the proof. The main goal of the proof is to construct, given a number
![]() $r\in \mathbb{N}$
and every sufficiently large
$r\in \mathbb{N}$
and every sufficiently large
![]() $k$
, a graph
$k$
, a graph
![]() $G$
on
$G$
on
![]() $n=s(k-1)+1$
vertices for some
$n=s(k-1)+1$
vertices for some
![]() $s \in \mathbb{N}$
, such that:
$s \in \mathbb{N}$
, such that:
-
(a) For every
 $v \in V(G)$
, there exists a partition of
$v \in V(G)$
, there exists a partition of
 $V(G)\setminus \{v\}$
into
$V(G)\setminus \{v\}$
into
 $k-1$
independent sets, each of size
$k-1$
independent sets, each of size
 $s$
, and
$s$
, and -
(b)
 $\alpha (G-R)=s$
for every
$\alpha (G-R)=s$
for every
 $R\subseteq E(G)$
of size at most
$R\subseteq E(G)$
of size at most
 $r$
.
$r$
.
The first property guarantees that
![]() $\chi (G-v)\le k-1$
for every
$\chi (G-v)\le k-1$
for every
![]() $v \in V(G)$
, while the second property guarantees that
$v \in V(G)$
, while the second property guarantees that
![]() $\chi (G-R)\ge \frac{n}{\alpha (G-R)}\ge \frac{s(k-1)+1}{s}\gt k-1$
for every set
$\chi (G-R)\ge \frac{n}{\alpha (G-R)}\ge \frac{s(k-1)+1}{s}\gt k-1$
for every set
![]() $R$
of at most
$R$
of at most
![]() $r$
edges. Hence,
$r$
edges. Hence,
![]() $G$
has the properties required for Theorem1.1. The way we will find such a graph
$G$
has the properties required for Theorem1.1. The way we will find such a graph
![]() $G$
is by looking for an
$G$
is by looking for an
![]() $s$
-uniform hypergraph
$s$
-uniform hypergraph
![]() $H$
on
$H$
on
![]() $n$
vertices with the following properties:
$n$
vertices with the following properties:
-
(a’)
 $H-v$
has a perfect matching for every
$H-v$
has a perfect matching for every
 $v \in V(H)$
, and
$v \in V(H)$
, and -
(b’) For every subset
 $X\subseteq V(H)$
of size
$X\subseteq V(H)$
of size
 $s+1$
there are more than
$s+1$
there are more than
 $r$
pairs of vertices in
$r$
pairs of vertices in
 $X$
that together are not included in any hyperedge of
$X$
that together are not included in any hyperedge of
 $H$
.
$H$
.
Once such a hypergraph is found, one can define
![]() $G$
as the graph with the same vertex-set as
$G$
as the graph with the same vertex-set as
![]() $H$
, in which two vertices are adjacent if and only if there is no hyperedge of
$H$
, in which two vertices are adjacent if and only if there is no hyperedge of
![]() $H$
that contains both of them. One can then easily verify that properties (a’), (b’) of
$H$
that contains both of them. One can then easily verify that properties (a’), (b’) of
![]() $H$
will imply the properties (a), (b) of
$H$
will imply the properties (a), (b) of
![]() $G$
, and hence
$G$
, and hence
![]() $G$
will be a suitable example for Theorem1.1.
$G$
will be a suitable example for Theorem1.1.
Finally, in order to construct such hypergraphs
![]() $H$
, the idea is to show that a suitably chosen binomial random
$H$
, the idea is to show that a suitably chosen binomial random
![]() $s$
-uniform hypergraph satisfies both properties simultaneously w.h.p. While (a’) can be easily deduced from the advances on Shamir’s hypergraph matching problem, verifying (b’) needs more technical work: We first show that w.h.p. the random binomial hypergraph is locally sparse, in the sense that there are not too many hyperedges concentrated on any small part of the hypergraph (Lemma 2.2 (ii)). The remaining technical work is then dedicated to proving Lemma 2.3, which says that every
$s$
-uniform hypergraph satisfies both properties simultaneously w.h.p. While (a’) can be easily deduced from the advances on Shamir’s hypergraph matching problem, verifying (b’) needs more technical work: We first show that w.h.p. the random binomial hypergraph is locally sparse, in the sense that there are not too many hyperedges concentrated on any small part of the hypergraph (Lemma 2.2 (ii)). The remaining technical work is then dedicated to proving Lemma 2.3, which says that every
![]() $s$
-uniform hypergraph satisfying the local sparsity condition has property (b’), where
$s$
-uniform hypergraph satisfying the local sparsity condition has property (b’), where
![]() $r$
grows with
$r$
grows with
![]() $s$
.
$s$
.
We now start with the details of the proof. In the following, given positive integers
![]() $n,k$
and a probability value
$n,k$
and a probability value
![]() $p \in [0,1]$
, we denote by
$p \in [0,1]$
, we denote by
![]() $\mathcal{H}_s(n,p)$
the binomial
$\mathcal{H}_s(n,p)$
the binomial
![]() $s$
-uniform random hypergraph on vertex-set
$s$
-uniform random hypergraph on vertex-set
![]() $V=[n]=\{1,\ldots, n\}$
, obtained by including every
$V=[n]=\{1,\ldots, n\}$
, obtained by including every
![]() $s$
-subset of
$s$
-subset of
![]() $V$
as a hyperedge independently with probability
$V$
as a hyperedge independently with probability
![]() $p$
. Given a hypergraph
$p$
. Given a hypergraph
![]() $H$
, a perfect matching of
$H$
, a perfect matching of
![]() $H$
is a collection
$H$
is a collection
![]() $\{e_1,\ldots, e_t\}\subseteq E(H)$
of hyperedges that form a set-partition of
$\{e_1,\ldots, e_t\}\subseteq E(H)$
of hyperedges that form a set-partition of
![]() $V(H)$
. Note that if
$V(H)$
. Note that if
![]() $H$
is an
$H$
is an
![]() $s$
-uniform hypergraph, then the existence of a perfect matching necessitates
$s$
-uniform hypergraph, then the existence of a perfect matching necessitates
![]() $|V(H)|\equiv 0 \text{ }(\text{mod }s)$
. One of the most famous problems in probabilistic graph theory for a long time was Shamir’s problem, that asked to determine the threshold for the random hypergraph
$|V(H)|\equiv 0 \text{ }(\text{mod }s)$
. One of the most famous problems in probabilistic graph theory for a long time was Shamir’s problem, that asked to determine the threshold for the random hypergraph
![]() $\mathcal{H}_s(n,p)$
with
$\mathcal{H}_s(n,p)$
with
![]() $n \equiv 0 \text{ }(\text{mod }s)$
to contain a perfect matching. This threshold was determined up to a multiplicative error in a breakthrough result by Johannson, Kahn and Vu [Reference Johansson, Kahn and Vu9] in 2008, as follows.
$n \equiv 0 \text{ }(\text{mod }s)$
to contain a perfect matching. This threshold was determined up to a multiplicative error in a breakthrough result by Johannson, Kahn and Vu [Reference Johansson, Kahn and Vu9] in 2008, as follows.
Theorem 2.1 (cf. [Reference Johansson, Kahn and Vu9]). For every integer
![]() $s \ge 1$
there exists a constant
$s \ge 1$
there exists a constant
![]() $C=C(s)\gt 0$
such that with
$C=C(s)\gt 0$
such that with
![]() $p=p(n)=\frac{C\log n}{n^{s-1}}$
it holds that
$p=p(n)=\frac{C\log n}{n^{s-1}}$
it holds that
![]() $\mathcal{H}_s(n,p)$
has a perfect matching w.h.p. provided that
$\mathcal{H}_s(n,p)$
has a perfect matching w.h.p. provided that
![]() $n \equiv 0 \text{ }(\text{mod }s)$
.
$n \equiv 0 \text{ }(\text{mod }s)$
.
It is worth noting that Theorem2.1 can alternatively be deduced from the recent resolution by Park and Pham [Reference Park and Pham11] of the Kahn-Kalai expectation-threshold conjecture. We further remark that recently, Kahn [Reference Kahn10] has determined the threshold in Shamir’s problem even more precisely, showing that taking
![]() $C=(1+o(1))(s-1)!$
is sufficient (and best-possible). We now use this probabilistic result to deduce the existence of uniform hypergraphs with special properties, as follows.
$C=(1+o(1))(s-1)!$
is sufficient (and best-possible). We now use this probabilistic result to deduce the existence of uniform hypergraphs with special properties, as follows.
Lemma 2.2.
Let
![]() $s \ge 2, m \ge 1$
be fixed integers. Then for every sufficiently large integer
$s \ge 2, m \ge 1$
be fixed integers. Then for every sufficiently large integer
![]() $n$
such that
$n$
such that
![]() $n \equiv 1 \text{ }(\text{mod }s)$
, there exists an
$n \equiv 1 \text{ }(\text{mod }s)$
, there exists an
![]() $s$
-uniform hypergraph
$s$
-uniform hypergraph
![]() $H$
on
$H$
on
![]() $n$
vertices with the following properties.
$n$
vertices with the following properties.
-
(i) For every
 $v \in V(H)$
, the hypergraph
$v \in V(H)$
, the hypergraph
 $H-v$
admits a perfect matching.
$H-v$
admits a perfect matching.
-
(ii) For every set
 $F\subseteq E(H)$
of hyperedges with
$F\subseteq E(H)$
of hyperedges with
 $|F|\le m$
, we have
$|F|\le m$
, we have
 \begin{equation*}\left |\bigcup _{e \in F}{e}\right |\ge (s-1)|F|.\end{equation*}
\begin{equation*}\left |\bigcup _{e \in F}{e}\right |\ge (s-1)|F|.\end{equation*}
Proof. Let
![]() $p(n)\, :\!= \frac{C\log n}{n^{s-1}}$
be as in the statement of Theorem2.1. Then, for every
$p(n)\, :\!= \frac{C\log n}{n^{s-1}}$
be as in the statement of Theorem2.1. Then, for every
![]() $n\equiv 1 \text{ }(\text{mod }s)$
chosen large enough, by Theorem2.1 we have
$n\equiv 1 \text{ }(\text{mod }s)$
chosen large enough, by Theorem2.1 we have
Now, define
![]() $q(n)\, :\!= \lceil 2\log _2(n)\rceil p(n-1)=\Theta \left (\frac{\log ^2 n}{n^{s-1}}\right )$
. In the following, we show that
$q(n)\, :\!= \lceil 2\log _2(n)\rceil p(n-1)=\Theta \left (\frac{\log ^2 n}{n^{s-1}}\right )$
. In the following, we show that
![]() $\mathcal{H}_s(n,q(n))$
satisfies both (i) and (ii) w.h.p. provided
$\mathcal{H}_s(n,q(n))$
satisfies both (i) and (ii) w.h.p. provided
![]() $n\equiv 1 \text{ }(\text{mod }s)$
, which will then imply the statement of the lemma.
$n\equiv 1 \text{ }(\text{mod }s)$
, which will then imply the statement of the lemma.
Consider sprinkling
![]() $l\, :\!= \lceil 2\log _2(n)\rceil$
independently generated copies
$l\, :\!= \lceil 2\log _2(n)\rceil$
independently generated copies
![]() $H_1,\ldots, H_l$
of
$H_1,\ldots, H_l$
of
![]() $\mathcal{H}_s(n,p(n-1))$
on vertex-set
$\mathcal{H}_s(n,p(n-1))$
on vertex-set
![]() $[n]$
. Their union
$[n]$
. Their union
![]() $\tilde{H}$
forms a binomial random hypergraph with edge-probability
$\tilde{H}$
forms a binomial random hypergraph with edge-probability
![]() $q'(n)\le l\cdot p(n-1)=q(n)$
. Now fix a vertex
$q'(n)\le l\cdot p(n-1)=q(n)$
. Now fix a vertex
![]() $v \in [n]$
. From the above we have
$v \in [n]$
. From the above we have
 \begin{align*} &\mathbb{P}(\mathcal{H}_s(n,q(n))-v \text{ has no perfect matching}) \\ \le \: & \mathbb{P}(\mathcal{H}_s(n,q'(n))-v \text{ has no perfect matching}) \\ = \: & \mathbb{P}(\tilde{H}-v \text{ has no perfect matching})\\ \le \: & \prod _{i=1}^{l}{\mathbb{P}(H_i-v\text{ has no perfect matching})}. \end{align*}
\begin{align*} &\mathbb{P}(\mathcal{H}_s(n,q(n))-v \text{ has no perfect matching}) \\ \le \: & \mathbb{P}(\mathcal{H}_s(n,q'(n))-v \text{ has no perfect matching}) \\ = \: & \mathbb{P}(\tilde{H}-v \text{ has no perfect matching})\\ \le \: & \prod _{i=1}^{l}{\mathbb{P}(H_i-v\text{ has no perfect matching})}. \end{align*}
By inequality 1, we have that
![]() $\mathbb{P}(H_i-v\text{ has no perfect matching})\le \frac{1}{2}$
for
$\mathbb{P}(H_i-v\text{ has no perfect matching})\le \frac{1}{2}$
for
![]() $i=1,\ldots, l$
. Altogether, it follows that the probability that
$i=1,\ldots, l$
. Altogether, it follows that the probability that
![]() $\mathcal{H}_s(n,q(n))-v$
has no perfect matching is at most
$\mathcal{H}_s(n,q(n))-v$
has no perfect matching is at most
![]() $\left (\frac{1}{2}\right )^{2\log _2(n)}=\frac{1}{n^2}$
. Hence, by a union bound over all choices of
$\left (\frac{1}{2}\right )^{2\log _2(n)}=\frac{1}{n^2}$
. Hence, by a union bound over all choices of
![]() $v$
, the probability that there exists a vertex
$v$
, the probability that there exists a vertex
![]() $v$
for which
$v$
for which
![]() $\mathcal{H}_s(n,q(n))-v$
has no perfect matching is at most
$\mathcal{H}_s(n,q(n))-v$
has no perfect matching is at most
![]() $\frac{1}{n}$
. Thus, w.h.p.
$\frac{1}{n}$
. Thus, w.h.p.
![]() $\mathcal{H}_s(n,q(n))$
satisfies property (i).
$\mathcal{H}_s(n,q(n))$
satisfies property (i).
Let us now move on to property (ii). For that purpose, we want to show that w.h.p. for every number
![]() $f=1,\ldots, m$
, no subset of
$f=1,\ldots, m$
, no subset of
![]() $[n]$
of size
$[n]$
of size
![]() $(s-1)f-1$
contains
$(s-1)f-1$
contains
![]() $f$
hyperedges from
$f$
hyperedges from
![]() $\mathcal{H}_s(n,q(n))$
. By a union bound over all configurations containing
$\mathcal{H}_s(n,q(n))$
. By a union bound over all configurations containing
![]() $(s-1)f-1$
vertices and
$(s-1)f-1$
vertices and
![]() $f$
hyperedges, we obtain that the probability that there exist
$f$
hyperedges, we obtain that the probability that there exist
![]() $f$
hyperedges in
$f$
hyperedges in
![]() $\mathcal{H}_s(n,q(n))$
spanning less than
$\mathcal{H}_s(n,q(n))$
spanning less than
![]() $(s-1)f$
vertices is at most
$(s-1)f$
vertices is at most
 \begin{equation*}\binom {n}{(s-1)f-1}\cdot O(1) \cdot q(n)^f=O\left (n^{(s-1)f-1}\cdot \left (\frac {\log ^2 n}{n^{s-1}}\right )^f\right )=O\left (\frac {\log ^{2f}n}{n}\right ).\end{equation*}
\begin{equation*}\binom {n}{(s-1)f-1}\cdot O(1) \cdot q(n)^f=O\left (n^{(s-1)f-1}\cdot \left (\frac {\log ^2 n}{n^{s-1}}\right )^f\right )=O\left (\frac {\log ^{2f}n}{n}\right ).\end{equation*}
Thus, w.h.p. we have that
![]() $\mathcal{H}_s(n,q(n))$
also satisfies item (ii) of the lemma. This concludes the proof.
$\mathcal{H}_s(n,q(n))$
also satisfies item (ii) of the lemma. This concludes the proof.
Next, we would like to use the hypergraphs from the previous lemma to construct graphs that satisfy the conditions of Theorem1.1. To do so, we need a technical result about the number of edges that can be spanned by any
![]() $(s+1)$
-subset of vertices in the so-called
$(s+1)$
-subset of vertices in the so-called
![]() $2$
-shadow of these hypergraphs, namely Lemma 2.3 below. Given a hypergraph
$2$
-shadow of these hypergraphs, namely Lemma 2.3 below. Given a hypergraph
![]() $H$
, its
$H$
, its
![]() $2$
-shadow is the graph
$2$
-shadow is the graph
![]() $G_2^H$
on the same vertex-set and where
$G_2^H$
on the same vertex-set and where
![]() $uv \in E(G_2^H)$
if and only if there is some
$uv \in E(G_2^H)$
if and only if there is some
![]() $e \in E(H)$
with
$e \in E(H)$
with
![]() $u,v \in e$
.
$u,v \in e$
.
Lemma 2.3.
Let
![]() $s$
be a positive integer, let
$s$
be a positive integer, let
![]() $H$
be an
$H$
be an
![]() $s$
-uniform hypergraph, and let
$s$
-uniform hypergraph, and let
![]() $G$
be the
$G$
be the
![]() $2$
-shadow of
$2$
-shadow of
![]() $H$
. If
$H$
. If
 \begin{equation*}\left |\bigcup _{e \in F}{e}\right | \ge (s-1)|F|\end{equation*}
\begin{equation*}\left |\bigcup _{e \in F}{e}\right | \ge (s-1)|F|\end{equation*}
holds for all
![]() $F \subseteq E(H)$
with
$F \subseteq E(H)$
with
![]() $|F|\lt 2^{s+1}$
, then
$|F|\lt 2^{s+1}$
, then
for all
![]() $X \subseteq V(G)$
of size
$X \subseteq V(G)$
of size
![]() $s+1$
.
$s+1$
.
To prove Lemma 2.3, we first establish an auxiliary result on hypergraphs in the form of Lemma 2.5 below, which in turn needs the following standard fact, a proof of which we include for completeness. In the following, we say that a hypergraph is connected, if its
![]() $2$
-shadow is connected as a graph.
$2$
-shadow is connected as a graph.
Observation 2.4.
Let
![]() $H=(V,E)$
be a connected hypergraph. Then
$H=(V,E)$
be a connected hypergraph. Then
Proof. Let
![]() $T$
be a spanning tree of
$T$
be a spanning tree of
![]() $G_2^H$
. For every edge
$G_2^H$
. For every edge
![]() $t \in E(T)$
, assign a hyperedge
$t \in E(T)$
, assign a hyperedge
![]() $e(t) \in E$
such that
$e(t) \in E$
such that
![]() $t \subseteq e(t)$
. For each
$t \subseteq e(t)$
. For each
![]() $e \in E$
, let
$e \in E$
, let
![]() $T_e\subseteq T$
be the forest induced by the edges
$T_e\subseteq T$
be the forest induced by the edges
![]() $\{t \in E(T)|e(t)=e\}$
. Clearly,
$\{t \in E(T)|e(t)=e\}$
. Clearly,
![]() $V(T_e)\subseteq e$
for every
$V(T_e)\subseteq e$
for every
![]() $e \in E$
, and thus
$e \in E$
, and thus
as desired.
Lemma 2.5.
Let
![]() $H=(V,E)$
be a hypergraph with
$H=(V,E)$
be a hypergraph with
![]() $|V|\ge 4$
and
$|V|\ge 4$
and
![]() $V \notin E$
. Suppose further that for every set
$V \notin E$
. Suppose further that for every set
![]() $F \subseteq E$
of hyperedges, we have
$F \subseteq E$
of hyperedges, we have
 \begin{equation*}\left |\bigcup _{e\in F}{e}\right |\ge \sum _{e\in F}{(|e|-1)}.\end{equation*}
\begin{equation*}\left |\bigcup _{e\in F}{e}\right |\ge \sum _{e\in F}{(|e|-1)}.\end{equation*}
Then there exists a set
![]() $W\subseteq V$
of size at most
$W\subseteq V$
of size at most
![]() $2$
such that
$2$
such that
![]() $G_2^H-W$
is disconnected.
$G_2^H-W$
is disconnected.
Proof. Suppose first that there exists at least one hyperedge
![]() $e_0 \in E$
with
$e_0 \in E$
with
![]() $|e_0|\ge 3$
. By assumption,
$|e_0|\ge 3$
. By assumption,
![]() $V \notin E$
, and thus there exists some vertex
$V \notin E$
, and thus there exists some vertex
![]() $v \in V\setminus e_0$
. Let us now consider the graph
$v \in V\setminus e_0$
. Let us now consider the graph
![]() $G=G_2^{H-e_0}$
, the
$G=G_2^{H-e_0}$
, the
![]() $2$
-shadow of the hypergraph
$2$
-shadow of the hypergraph
![]() $H-e_0$
obtained from
$H-e_0$
obtained from
![]() $H$
by deleting
$H$
by deleting
![]() $e_0$
. Let
$e_0$
. Let
![]() $C$
be the vertex-set of the unique connected component of
$C$
be the vertex-set of the unique connected component of
![]() $G$
that contains
$G$
that contains
![]() $v$
. We claim that
$v$
. We claim that
![]() $|C \cap e_0|\le 2$
. To that end, define
$|C \cap e_0|\le 2$
. To that end, define
![]() $F$
as the set of hyperedges of
$F$
as the set of hyperedges of
![]() $H-e_0$
that are contained in
$H-e_0$
that are contained in
![]() $C$
. Note that, since every hyperedge
$C$
. Note that, since every hyperedge
![]() $e\in E\setminus \{e_0\}$
induces a clique in
$e\in E\setminus \{e_0\}$
induces a clique in
![]() $G$
, we have that
$G$
, we have that
![]() $\bigcup _{e\in F}{e}=C$
and that the hypergraph
$\bigcup _{e\in F}{e}=C$
and that the hypergraph
![]() $H'=(C,F)$
is connected. These facts imply via Observation 2.4 that
$H'=(C,F)$
is connected. These facts imply via Observation 2.4 that
 \begin{equation*}\left |\bigcup _{e\in F}{e}\right |=|C|\le 1+\sum _{e \in F}{(|e|-1)}.\end{equation*}
\begin{equation*}\left |\bigcup _{e\in F}{e}\right |=|C|\le 1+\sum _{e \in F}{(|e|-1)}.\end{equation*}
On the other hand, by applying the assumption of the lemma to the edge-set
![]() $F \cup \{e_0\}$
, we find
$F \cup \{e_0\}$
, we find
 \begin{equation*}\sum _{e \in F\cup \{e_0\}}{(|e|-1)}\le \left |e_0 \cup \bigcup _{e\in F}{e}\right |=|e_0 \cup C|=|e_0|+|C|-|e_0 \cap C|.\end{equation*}
\begin{equation*}\sum _{e \in F\cup \{e_0\}}{(|e|-1)}\le \left |e_0 \cup \bigcup _{e\in F}{e}\right |=|e_0 \cup C|=|e_0|+|C|-|e_0 \cap C|.\end{equation*}
Subtracting
![]() $(|e_0|-1)$
from both sides yields
$(|e_0|-1)$
from both sides yields
Plugging the above into the first inequality we get
![]() $|C|\le |C|+2-|e_0 \cap C|,$
and thus
$|C|\le |C|+2-|e_0 \cap C|,$
and thus
![]() $|e_0 \cap C|\le 2$
, as claimed. We now set
$|e_0 \cap C|\le 2$
, as claimed. We now set
![]() $W\, :\!= e_0\cap C$
and claim that
$W\, :\!= e_0\cap C$
and claim that
![]() $G_2^H-W$
is disconnected. Indeed, it follows readily from the definition of
$G_2^H-W$
is disconnected. Indeed, it follows readily from the definition of
![]() $C$
that no edge in
$C$
that no edge in
![]() $G_2^H-W$
connects a vertex in
$G_2^H-W$
connects a vertex in
![]() $C\setminus W=C\setminus e_0$
to a vertex in
$C\setminus W=C\setminus e_0$
to a vertex in
![]() $V\setminus C$
. Further, since
$V\setminus C$
. Further, since
![]() $v \in C\setminus e_0$
we have that the first set is non-empty, and since
$v \in C\setminus e_0$
we have that the first set is non-empty, and since
![]() $|V\setminus C|\ge |e_0\setminus C|=|e_0|-|e_0\cap C|\ge 3-2=1\gt 0$
, the second set is also non-empty. Thus,
$|V\setminus C|\ge |e_0\setminus C|=|e_0|-|e_0\cap C|\ge 3-2=1\gt 0$
, the second set is also non-empty. Thus,
![]() $G_2^H-W$
is indeed disconnected, which concludes the proof in this case.
$G_2^H-W$
is indeed disconnected, which concludes the proof in this case.
For the second case, assume that
![]() $|e|\le 2$
for every
$|e|\le 2$
for every
![]() $e \in E$
. W.l.o.g. (since they do not have an effect on
$e \in E$
. W.l.o.g. (since they do not have an effect on
![]() $G_2^H$
) we may assume that
$G_2^H$
) we may assume that
![]() $H$
contains no hyperedges of size
$H$
contains no hyperedges of size
![]() $1$
, i.e.,
$1$
, i.e.,
![]() $H$
is a graph and
$H$
is a graph and
![]() $G_2^H=H$
. If
$G_2^H=H$
. If
![]() $H$
has a vertex of degree at most
$H$
has a vertex of degree at most
![]() $1$
, then the statement of the lemma trivially holds, so suppose that
$1$
, then the statement of the lemma trivially holds, so suppose that
![]() $H$
has minimum degree at least
$H$
has minimum degree at least
![]() $2$
. The condition of the lemma now yields
$2$
. The condition of the lemma now yields
![]() $|E|=\sum _{e\in E}{(|e|-1)}\le |\bigcup _{e\in E}{e}|\le |V|$
. This directly implies via the handshake-lemma that
$|E|=\sum _{e\in E}{(|e|-1)}\le |\bigcup _{e\in E}{e}|\le |V|$
. This directly implies via the handshake-lemma that
![]() $H$
is a
$H$
is a
![]() $2$
-regular graph. It is trivial to see that every such graph on at least
$2$
-regular graph. It is trivial to see that every such graph on at least
![]() $4$
vertices contains a cut-set
$4$
vertices contains a cut-set
![]() $W$
consisting of at most
$W$
consisting of at most
![]() $2$
vertices, and this concludes the proof.
$2$
vertices, and this concludes the proof.
We are now ready to present the proof of Lemma 2.3. The main idea is to use that by Lemma 2.5, the subgraph of the
![]() $2$
-shadow of
$2$
-shadow of
![]() $H$
induced on any subset of
$H$
induced on any subset of
![]() $s+1$
vertices must contain a cut consisting of
$s+1$
vertices must contain a cut consisting of
![]() $2$
vertices, which then ensures that this graph must have a substantial number of non-edges.
$2$
vertices, which then ensures that this graph must have a substantial number of non-edges.
Proof of
Lemma 2.3. The statement of the lemma holds trivially when
![]() $s\in \{1,2\}$
, so suppose
$s\in \{1,2\}$
, so suppose
![]() $s\ge 3$
in the following. Let us consider the hypergraph
$s\ge 3$
in the following. Let us consider the hypergraph
![]() $H_X$
obtained by restricting
$H_X$
obtained by restricting
![]() $H$
to
$H$
to
![]() $X$
, and note that the
$X$
, and note that the
![]() $2$
-shadow of
$2$
-shadow of
![]() $H_X$
equals
$H_X$
equals
![]() $G[X]$
. Further note that for every subset
$G[X]$
. Further note that for every subset
![]() $F \subseteq E(H)$
of size less than
$F \subseteq E(H)$
of size less than
![]() $2^{s+1}$
, it holds that
$2^{s+1}$
, it holds that
 \begin{equation*}\left |\bigcup _{e \in F}{(e\cap X)}\right |\ge \left |\bigcup _{e \in F}{e}\right |-\sum _{e \in F}{|e\setminus X|}\end{equation*}
\begin{equation*}\left |\bigcup _{e \in F}{(e\cap X)}\right |\ge \left |\bigcup _{e \in F}{e}\right |-\sum _{e \in F}{|e\setminus X|}\end{equation*}
This directly implies that
![]() $\left |\bigcup _{e \in F}{e}\right |\ge \sum _{e \in F}{(|e|-1)}$
for every subset
$\left |\bigcup _{e \in F}{e}\right |\ge \sum _{e \in F}{(|e|-1)}$
for every subset
![]() $F \subseteq E(H_X)$
. We can therefore apply Lemma 2.5, which implies that there exists a set
$F \subseteq E(H_X)$
. We can therefore apply Lemma 2.5, which implies that there exists a set
![]() $W\subseteq X$
of size at most
$W\subseteq X$
of size at most
![]() $2$
such that
$2$
such that
![]() $G[X]-W$
is disconnected. Thus, there exist disjoint non-empty sets
$G[X]-W$
is disconnected. Thus, there exist disjoint non-empty sets
![]() $A, B$
such that
$A, B$
such that
![]() $A\cup B=X\setminus W$
and no edge in
$A\cup B=X\setminus W$
and no edge in
![]() $G[X]$
connects
$G[X]$
connects
![]() $A$
and
$A$
and
![]() $B$
. Note that as
$B$
. Note that as
![]() $|A|,|B|\ge 1$
and
$|A|,|B|\ge 1$
and
![]() $|A|+|B|=|X|-|W|\ge (s+1)-2=s-1$
, we have
$|A|+|B|=|X|-|W|\ge (s+1)-2=s-1$
, we have
![]() $|A||B|\ge s-2$
. We conclude that
$|A||B|\ge s-2$
. We conclude that
This concludes the proof.
Proof of
Theorem 1.1. Let an integer
![]() $r \ge 1$
be given. Define
$r \ge 1$
be given. Define
![]() $s\, :\!= r+3$
and
$s\, :\!= r+3$
and
![]() $m\, :\!= 2^{s+1}$
. By Lemma 2.3 there exists some
$m\, :\!= 2^{s+1}$
. By Lemma 2.3 there exists some
![]() $n_0 \in \mathbb{N}$
such that for every integer
$n_0 \in \mathbb{N}$
such that for every integer
![]() $n \ge n_0$
with
$n \ge n_0$
with
![]() $n \equiv 1 \text{ }(\text{mod }s)$
, there exists an
$n \equiv 1 \text{ }(\text{mod }s)$
, there exists an
![]() $s$
-uniform hypergraph
$s$
-uniform hypergraph
![]() $H$
on
$H$
on
![]() $n$
vertices with the following properties.
$n$
vertices with the following properties.
-
• For every
 $v \in V(H)$
, the hypergraph
$v \in V(H)$
, the hypergraph
 $H-v$
admits a perfect matching.
$H-v$
admits a perfect matching. -
• For every set
 $F\subseteq E(H)$
of hyperedges with
$F\subseteq E(H)$
of hyperedges with
 $|F|\le m=2^{s+1}$
, we have
$|F|\le m=2^{s+1}$
, we have \begin{equation*}\left |\bigcup _{e \in F}{e}\right |\ge (s-1)|F|.\end{equation*}
\begin{equation*}\left |\bigcup _{e \in F}{e}\right |\ge (s-1)|F|.\end{equation*}
Define
![]() $k_0\, :\!= \lceil \frac{n_0-1}{s}\rceil +1$
and let
$k_0\, :\!= \lceil \frac{n_0-1}{s}\rceil +1$
and let
![]() $k \ge k_0$
be any given integer. Let
$k \ge k_0$
be any given integer. Let
![]() $H$
be an
$H$
be an
![]() $s$
-uniform hypergraph on
$s$
-uniform hypergraph on
![]() $n\, :\!= s(k-1)+1\ge n_0$
vertices satisfying the properties above. Finally, we define a graph
$n\, :\!= s(k-1)+1\ge n_0$
vertices satisfying the properties above. Finally, we define a graph
![]() $G$
as the complement of the
$G$
as the complement of the
![]() $2$
-shadow
$2$
-shadow
![]() $G_2^H$
of
$G_2^H$
of
![]() $H$
. We claim that it satisfies the properties required by the theorem, that is,
$H$
. We claim that it satisfies the properties required by the theorem, that is,
-
•
 $G-v$
is
$G-v$
is
 $(k-1)$
-colourable for every
$(k-1)$
-colourable for every
 $v \in V(G)$
, and
$v \in V(G)$
, and -
• for every set
 $R \subseteq E(G)$
of edges with
$R \subseteq E(G)$
of edges with
 $|R|\le r$
, we have
$|R|\le r$
, we have
 $\chi (G-R)\ge k$
.
$\chi (G-R)\ge k$
.
To verify the first statement, consider any vertex
![]() $v$
and a perfect matching of
$v$
and a perfect matching of
![]() $H-v$
. Since
$H-v$
. Since
![]() $H$
is
$H$
is
![]() $s$
-uniform, the perfect matching forms a partition of
$s$
-uniform, the perfect matching forms a partition of
![]() $V(H)\setminus \{v\}=V(G)\setminus \{v\}$
into
$V(H)\setminus \{v\}=V(G)\setminus \{v\}$
into
![]() $\frac{n-1}{s}=k-1$
sets, each inducing a hyperedge in
$\frac{n-1}{s}=k-1$
sets, each inducing a hyperedge in
![]() $H$
and thus an independent set in
$H$
and thus an independent set in
![]() $G$
. Hence we have
$G$
. Hence we have
![]() $\chi (G-v)\le k-1$
.
$\chi (G-v)\le k-1$
.
Now let
![]() $R \subseteq E(G)$
with
$R \subseteq E(G)$
with
![]() $|R|\le r$
be given. We claim that
$|R|\le r$
be given. We claim that
![]() $\alpha (G-R)\le s$
, i.e., that there exists no independent set in
$\alpha (G-R)\le s$
, i.e., that there exists no independent set in
![]() $G-R$
of size
$G-R$
of size
![]() $s+1$
, which will then imply
$s+1$
, which will then imply
![]() $\chi (G-R)\ge \frac{n}{\alpha (G-R)}\ge \frac{n}{s}\gt k-1$
, as desired. Suppose towards a contradiction that there is some
$\chi (G-R)\ge \frac{n}{\alpha (G-R)}\ge \frac{n}{s}\gt k-1$
, as desired. Suppose towards a contradiction that there is some
![]() $X\subseteq V(G)$
of size
$X\subseteq V(G)$
of size
![]() $s+1$
that is independent in
$s+1$
that is independent in
![]() $G-R$
. Then
$G-R$
. Then
![]() $G[X]$
contains at most
$G[X]$
contains at most
![]() $r$
edges, and thus its complement graph, namely
$r$
edges, and thus its complement graph, namely
![]() $G_2^H[X]$
, contains at least
$G_2^H[X]$
, contains at least
![]() $\binom{s+1}{2}-r=\binom{s}{2}+s-r=\binom{s}{2}+3$
edges. However, by Lemma 2.3 applied to
$\binom{s+1}{2}-r=\binom{s}{2}+s-r=\binom{s}{2}+3$
edges. However, by Lemma 2.3 applied to
![]() $H$
, we find that
$H$
, we find that
![]() $|E(G_2^H[X])|\le \binom{s}{2}+2$
, a contradiction. This shows that indeed,
$|E(G_2^H[X])|\le \binom{s}{2}+2$
, a contradiction. This shows that indeed,
![]() $\alpha (G-R)\le s$
for every
$\alpha (G-R)\le s$
for every
![]() $R \subseteq E(G)$
with
$R \subseteq E(G)$
with
![]() $|R|\le r$
, concluding the proof.
$|R|\le r$
, concluding the proof.