No CrossRef data available.
Article contents
G-Intersection Theorems for Matchings and Other Graphs
Published online by Cambridge University Press: 01 July 2008
Abstract
If G is a graph with vertex set [n] then  is G-intersecting if, for all
is G-intersecting if, for all 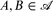 , either A ∩ B ≠ ∅ or there exist a ∈ A and b ∈ B such that a ~Gb.
, either A ∩ B ≠ ∅ or there exist a ∈ A and b ∈ B such that a ~Gb.
The question of how large a k-uniform G-intersecting family can be was first considered by Bohman, Frieze, Ruszinkó and Thoma [2], who identified two natural candidates for the extrema depending on the relative sizes of k and n and asked whether there is a sharp phase transition between the two. Our first result shows that there is a sharp transition and characterizes the extremal families when G is a matching. We also give an example demonstrating that other extremal families can occur.
Our second result gives a sufficient condition for the largest G-intersecting family to contain almost all k-sets. In particular we show that if Cn is the n-cycle and k > αn + o(n), where α = 0.266. . . is the smallest positive root of (1 − x)3(1 + x) = 1/2, then the largest Cn-intersecting family has size 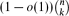 .
.
Finally we consider the non-uniform problem, and show that in this case the size of the largest G-intersecting family depends on the matching number of G.
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2008


