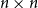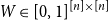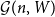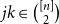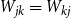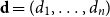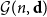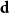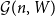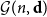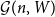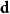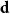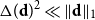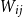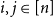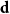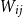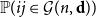1. Introduction
Given a realisable degree sequence
![]() $\textbf{d} = (d_1, \ldots, d_n)$
(a degree sequence
$\textbf{d} = (d_1, \ldots, d_n)$
(a degree sequence
![]() $\textbf{d}$
is realisable if there exists a simple graph with degree sequence
$\textbf{d}$
is realisable if there exists a simple graph with degree sequence
![]() $\textbf{d}$
), let
$\textbf{d}$
), let
![]() ${\mathcal G}(n,\textbf{d})$
denote a random graph chosen uniformly from the set of graphs on
${\mathcal G}(n,\textbf{d})$
denote a random graph chosen uniformly from the set of graphs on
![]() $[n]$
where vertex
$[n]$
where vertex
![]() $i$
has degree
$i$
has degree
![]() $d_i$
. Random graphs with a specified degree sequence are a popular class of random graphs used in many fields of research such as social network modelling and analysis [Reference Lusher, Koskinen and Robins29, Reference Morris, O’Neal and Deckro33], epidemic analysis [Reference Bohman and Picollelli5], and network sciences [Reference Chung and Lu9, Reference Newman, Strogatz and Watts34, Reference Van Der Hofstad35]. While these random graphs have been extensively used to model and analyse real-world networks, such as social networks and the internet, they present several analytical challenges. The most prominent difficulties in analysing
$d_i$
. Random graphs with a specified degree sequence are a popular class of random graphs used in many fields of research such as social network modelling and analysis [Reference Lusher, Koskinen and Robins29, Reference Morris, O’Neal and Deckro33], epidemic analysis [Reference Bohman and Picollelli5], and network sciences [Reference Chung and Lu9, Reference Newman, Strogatz and Watts34, Reference Van Der Hofstad35]. While these random graphs have been extensively used to model and analyse real-world networks, such as social networks and the internet, they present several analytical challenges. The most prominent difficulties in analysing
![]() ${\mathcal G}(n,\textbf{d})$
are evaluating the edge probabilities and dealing with edge dependencies. Compared with the classical Erdős–Rényi random graph
${\mathcal G}(n,\textbf{d})$
are evaluating the edge probabilities and dealing with edge dependencies. Compared with the classical Erdős–Rényi random graph
![]() ${\mathcal G}(n,p)$
where every edge
${\mathcal G}(n,p)$
where every edge
![]() $jk\in \binom{[n]}{2}$
appears independently with probability
$jk\in \binom{[n]}{2}$
appears independently with probability
![]() $p$
, there is no known closed formula for
$p$
, there is no known closed formula for
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
for general
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
for general
![]() $\textbf{d}$
. Although asymptotic formulas exist for
$\textbf{d}$
. Although asymptotic formulas exist for
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
for some classes of
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
for some classes of
![]() $\textbf{d}$
, the correlation between the edges poses additional challenges when estimating the probabilities of events in
$\textbf{d}$
, the correlation between the edges poses additional challenges when estimating the probabilities of events in
![]() ${\mathcal G}(n,\textbf{d})$
.
${\mathcal G}(n,\textbf{d})$
.
We denote
![]() ${\mathcal G}(n,\textbf{d})$
by
${\mathcal G}(n,\textbf{d})$
by
![]() ${\mathcal G}(n,d)$
when
${\mathcal G}(n,d)$
when
![]() $\textbf{d}=(d,d,\ldots, d)$
, that is,
$\textbf{d}=(d,d,\ldots, d)$
, that is,
![]() $\textbf{d}$
is a
$\textbf{d}$
is a
![]() $d$
-regular degree sequence. The random regular graph
$d$
-regular degree sequence. The random regular graph
![]() ${\mathcal G}(n,d)$
is the most well-understood model among all
${\mathcal G}(n,d)$
is the most well-understood model among all
![]() ${\mathcal G}(n,\textbf{d})$
. For instance, the asymptotic enumeration of
${\mathcal G}(n,\textbf{d})$
. For instance, the asymptotic enumeration of
![]() $d$
-regular graphs on
$d$
-regular graphs on
![]() $n$
vertices has been completely solved following a sequence of benchmark research [Reference Barvinok2–Reference Bender and Canfield4, Reference Bollobás6, Reference Liebenau and Wormald28, Reference McKay30–Reference McKay and Wormald32]. Properties and graph parameters of random regular graphs have been extensively studied, including Hamiltonicity, the chromatic and list chromatic numbers, independence number, and the distribution of subgraphs in
$n$
vertices has been completely solved following a sequence of benchmark research [Reference Barvinok2–Reference Bender and Canfield4, Reference Bollobás6, Reference Liebenau and Wormald28, Reference McKay30–Reference McKay and Wormald32]. Properties and graph parameters of random regular graphs have been extensively studied, including Hamiltonicity, the chromatic and list chromatic numbers, independence number, and the distribution of subgraphs in
![]() ${\mathcal G}(n,d)$
[Reference Cooper, Frieze and Reed13, Reference Cooper, Frieze and Reed13, Reference Gao and Wormald22, Reference Krivelevich, Sudakov, Vu and Wormald27]. We refer the interested readers to a survey of Wormald [Reference Wormald36] for many other properties of random regular graphs. However, in general
${\mathcal G}(n,d)$
[Reference Cooper, Frieze and Reed13, Reference Cooper, Frieze and Reed13, Reference Gao and Wormald22, Reference Krivelevich, Sudakov, Vu and Wormald27]. We refer the interested readers to a survey of Wormald [Reference Wormald36] for many other properties of random regular graphs. However, in general
![]() $\textbf{d}$
can vary from near-regular sequences to heavy-tailed sequences such as power-law sequences. Both enumerating graphs of given degree sequences and analysing properties such as connectivity or Hamiltonicity of
$\textbf{d}$
can vary from near-regular sequences to heavy-tailed sequences such as power-law sequences. Both enumerating graphs of given degree sequences and analysing properties such as connectivity or Hamiltonicity of
![]() ${\mathcal G}(n,\textbf{d})$
turn out to be challenging, and there are many open problems in this field. In 2004 Kim and Vu proposed the sandwich conjecture, which informally says that
${\mathcal G}(n,\textbf{d})$
turn out to be challenging, and there are many open problems in this field. In 2004 Kim and Vu proposed the sandwich conjecture, which informally says that
![]() ${\mathcal G}(n,d)$
can be well approximated by
${\mathcal G}(n,d)$
can be well approximated by
![]() ${\mathcal G}(n,p=d/n)$
through sandwiching
${\mathcal G}(n,p=d/n)$
through sandwiching
![]() ${\mathcal G}(n,d)$
between two correlated copies of
${\mathcal G}(n,d)$
between two correlated copies of
![]() ${\mathcal G}(n,p)$
, one with
${\mathcal G}(n,p)$
, one with
![]() $p$
slightly smaller than
$p$
slightly smaller than
![]() $d/n$
and the other with
$d/n$
and the other with
![]() $p$
slightly greater than
$p$
slightly greater than
![]() $d/n$
. To formally state the conjecture, we define a coupling of a finite set of random variables (or graphs)
$d/n$
. To formally state the conjecture, we define a coupling of a finite set of random variables (or graphs)
![]() $Z_1,\ldots, Z_k$
as a
$Z_1,\ldots, Z_k$
as a
![]() $k$
-tuple of random variables
$k$
-tuple of random variables
![]() $(\hat Z_1,\ldots, \hat Z_k)$
defined in the same probability space such that the marginal distribution of
$(\hat Z_1,\ldots, \hat Z_k)$
defined in the same probability space such that the marginal distribution of
![]() $\hat Z_i$
is the same as the distribution of
$\hat Z_i$
is the same as the distribution of
![]() $Z_i$
for every
$Z_i$
for every
![]() $1\le i\le k$
. The sandwich conjecture is about a 3-tuple coupling of random graphs, proposed by Kim and Vu, given as below. The standard Landau notation is used, and a formal definition of the notation is given before Section 1.1.
$1\le i\le k$
. The sandwich conjecture is about a 3-tuple coupling of random graphs, proposed by Kim and Vu, given as below. The standard Landau notation is used, and a formal definition of the notation is given before Section 1.1.
Conjecture 1.1 ([Reference Kim and Vu25]). For
![]() $d\gg \log n$
, there exist probabilities
$d\gg \log n$
, there exist probabilities
![]() $p_1,p_2=(1+o(1))d/n$
and a coupling
$p_1,p_2=(1+o(1))d/n$
and a coupling
![]() $(G_L, G, G_U)$
such that marginally,
$(G_L, G, G_U)$
such that marginally,
![]() $G_L\sim{\mathcal G}(n,p_1)$
,
$G_L\sim{\mathcal G}(n,p_1)$
,
![]() $G\sim{\mathcal G}(n,d)$
,
$G\sim{\mathcal G}(n,d)$
,
![]() $G_U\sim{\mathcal G}(n,p_2)$
and jointly,
$G_U\sim{\mathcal G}(n,p_2)$
and jointly,
![]() ${\mathbb P}(G_L\subseteq G\subseteq G_U)=1-o(1)$
.
${\mathbb P}(G_L\subseteq G\subseteq G_U)=1-o(1)$
.
The sandwich conjecture, if proved to be true, is a powerful tool for analysing
![]() ${\mathcal G}(n,d)$
, and reveals beautiful distributional relations between the two different random graph models. The assumption
${\mathcal G}(n,d)$
, and reveals beautiful distributional relations between the two different random graph models. The assumption
![]() $d\gg \log n$
is necessary, as for
$d\gg \log n$
is necessary, as for
![]() $p=O(\log n/n)$
, the maximum and minimum degrees of
$p=O(\log n/n)$
, the maximum and minimum degrees of
![]() ${\mathcal G}(n,p)$
differ by some constant factor away from 1, making it impossible for the sandwich conjecture to hold. For simplicity, we refer to a coupling
${\mathcal G}(n,p)$
differ by some constant factor away from 1, making it impossible for the sandwich conjecture to hold. For simplicity, we refer to a coupling
![]() $({\mathcal G}_n^1,{\mathcal G}_n^2)$
of two random graphs
$({\mathcal G}_n^1,{\mathcal G}_n^2)$
of two random graphs
![]() ${\mathcal G}_n^{1}$
and
${\mathcal G}_n^{1}$
and
![]() ${\mathcal G}_n^{2}$
as embedding
${\mathcal G}_n^{2}$
as embedding
![]() ${\mathcal G}_n^1$
into
${\mathcal G}_n^1$
into
![]() ${\mathcal G}_n^2$
, if in the coupling
${\mathcal G}_n^2$
, if in the coupling
![]() ${\mathcal G}_n^1$
is a subgraph of
${\mathcal G}_n^1$
is a subgraph of
![]() ${\mathcal G}_n^2$
with probability going to 1 as
${\mathcal G}_n^2$
with probability going to 1 as
![]() $n\to \infty$
. It turns out that embedding
$n\to \infty$
. It turns out that embedding
![]() ${\mathcal G}(n,d)$
into
${\mathcal G}(n,d)$
into
![]() ${\mathcal G}(n,p=(1+o(1))d/n)$
is much more difficult than embedding
${\mathcal G}(n,p=(1+o(1))d/n)$
is much more difficult than embedding
![]() ${\mathcal G}(n,p=(1-o(1))d/n)$
into
${\mathcal G}(n,p=(1-o(1))d/n)$
into
![]() ${\mathcal G}(n,d)$
. In their paper [Reference Kim and Vu25], Kim and Vu established an embedding of
${\mathcal G}(n,d)$
. In their paper [Reference Kim and Vu25], Kim and Vu established an embedding of
![]() ${\mathcal G}(n,p=(1-o(1))d/n)$
into
${\mathcal G}(n,p=(1-o(1))d/n)$
into
![]() ${\mathcal G}(n,d)$
for
${\mathcal G}(n,d)$
for
![]() $d$
up to approximately
$d$
up to approximately
![]() $n^{1/3}$
(and
$n^{1/3}$
(and
![]() $d\gg \log n$
). Subsequent work by Dudek, Frieze, Ruciński, and Šileikis [Reference Dudek, Frieze, Ruciński and Šileikis14] improved this result to
$d\gg \log n$
). Subsequent work by Dudek, Frieze, Ruciński, and Šileikis [Reference Dudek, Frieze, Ruciński and Šileikis14] improved this result to
![]() $d=o(n)$
, and extended it to random uniform hypergraphs as well. The first 2-side sandwich theorem was proved by Isaev, McKay, and the first author [Reference Gao, Isaev and McKay17, Reference Gao, Isaev and McKay18] in the case that
$d=o(n)$
, and extended it to random uniform hypergraphs as well. The first 2-side sandwich theorem was proved by Isaev, McKay, and the first author [Reference Gao, Isaev and McKay17, Reference Gao, Isaev and McKay18] in the case that
![]() $d$
is linear in
$d$
is linear in
![]() $n$
. Klimosová, Reiher, Ruciński, and Šileikis [Reference Klimošová, Reiher, Ruciński and Šileikis26] proved the sandwich conjecture for
$n$
. Klimosová, Reiher, Ruciński, and Šileikis [Reference Klimošová, Reiher, Ruciński and Šileikis26] proved the sandwich conjecture for
![]() $d\gg (n\log n)^{3/4}$
. Finally Isaev, McKay, and the first author [Reference Gao, Isaev and McKay19] confirmed the sandwich conjecture for all
$d\gg (n\log n)^{3/4}$
. Finally Isaev, McKay, and the first author [Reference Gao, Isaev and McKay19] confirmed the sandwich conjecture for all
![]() $d\ge \log ^4 n$
. It is worth noting that a more general sandwich theorem was presented in [Reference Gao, Isaev and McKay17–Reference Gao, Isaev and McKay19] for random graphs
$d\ge \log ^4 n$
. It is worth noting that a more general sandwich theorem was presented in [Reference Gao, Isaev and McKay17–Reference Gao, Isaev and McKay19] for random graphs
![]() ${\mathcal G}(n,\textbf{d})$
where
${\mathcal G}(n,\textbf{d})$
where
![]() $\textbf{d}$
is a near-regular degree sequence, where all degrees are asymptotically equal.
$\textbf{d}$
is a near-regular degree sequence, where all degrees are asymptotically equal.
While it is not possible to approximate
![]() ${\mathcal G}(n,\textbf{d})$
by
${\mathcal G}(n,\textbf{d})$
by
![]() ${\mathcal G}(n,p)$
in a useful way for more general forms of
${\mathcal G}(n,p)$
in a useful way for more general forms of
![]() $\textbf{d}$
(since the typical degree distribution of
$\textbf{d}$
(since the typical degree distribution of
![]() ${\mathcal G}(n,p)$
would be very different from
${\mathcal G}(n,p)$
would be very different from
![]() $\textbf{d}$
), a natural alternative is to consider a generalised Erdös–Rényi graph
$\textbf{d}$
), a natural alternative is to consider a generalised Erdös–Rényi graph
![]() ${\mathcal G}(n,W)$
, where
${\mathcal G}(n,W)$
, where
![]() $W$
is a symmetric
$W$
is a symmetric
![]() $n\times n$
matrix. In this model, each edge
$n\times n$
matrix. In this model, each edge
![]() $jk\in \binom{[n]}{2}$
appears in
$jk\in \binom{[n]}{2}$
appears in
![]() ${\mathcal G}(n,W)$
independently with probability
${\mathcal G}(n,W)$
independently with probability
![]() $W_{jk}$
. By choosing different forms of
$W_{jk}$
. By choosing different forms of
![]() $W$
, we can recover well-studied models in the literature, such as
$W$
, we can recover well-studied models in the literature, such as
![]() ${\mathcal G}(n,p)$
, the Chung–Lu model [Reference Chung and Lu9–Reference Chung, Lu and Vu12], the
${\mathcal G}(n,p)$
, the Chung–Lu model [Reference Chung and Lu9–Reference Chung, Lu and Vu12], the
![]() $\boldsymbol{\beta }$
-model [Reference Chatterjee, Diaconis and Sly8, Reference Isaev and McKay24], and the stochastic block model [Reference Holland, Laskey and Leinhardt23].
$\boldsymbol{\beta }$
-model [Reference Chatterjee, Diaconis and Sly8, Reference Isaev and McKay24], and the stochastic block model [Reference Holland, Laskey and Leinhardt23].
The objective of this paper is to establish an embedding of
![]() ${\mathcal G}(n,W)$
into
${\mathcal G}(n,W)$
into
![]() ${\mathcal G}(n,\textbf{d})$
, where
${\mathcal G}(n,\textbf{d})$
, where
![]() $\textbf{d}$
is a degree sequence that may deviate significantly from being regular, for a suitable choice of
$\textbf{d}$
is a degree sequence that may deviate significantly from being regular, for a suitable choice of
![]() $W$
. What constitutes a good
$W$
. What constitutes a good
![]() $W$
? Intuitively one would like the entry
$W$
? Intuitively one would like the entry
![]() $W_{jk}$
to be approximately
$W_{jk}$
to be approximately
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
, the true probability that
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
, the true probability that
![]() $jk$
is an edge in
$jk$
is an edge in
![]() ${\mathcal G}(n,\textbf{d})$
. To formalise this notion, we define
${\mathcal G}(n,\textbf{d})$
. To formalise this notion, we define
![]() $W^*=W^*(\textbf{d})$
as the
$W^*=W^*(\textbf{d})$
as the
![]() $n\times n$
matrix where
$n\times n$
matrix where
![]() $W^*_{jk}={\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
for every
$W^*_{jk}={\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
for every
![]() $i,j\in [n]$
.
$i,j\in [n]$
.
Question 1.2.
Given
![]() $\textbf{d}$
, does there exists
$\textbf{d}$
, does there exists
![]() $W=(1-o(1))W^*(\textbf{d})$
such that
$W=(1-o(1))W^*(\textbf{d})$
such that
![]() ${\mathcal G}(n,W)$
can be embedded into
${\mathcal G}(n,W)$
can be embedded into
![]() ${\mathcal G}(n,\textbf{d})$
?
${\mathcal G}(n,\textbf{d})$
?
Note that the asymptotic value of
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
is not known for all realisable degree sequences
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
is not known for all realisable degree sequences
![]() $\textbf{d}$
. The coupling scheme we use in this paper heavily relies on the expression of the asymptotic formula for
$\textbf{d}$
. The coupling scheme we use in this paper heavily relies on the expression of the asymptotic formula for
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
. Therefore, we are restricted to degree sequences for which an asymptotic evaluation of
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
. Therefore, we are restricted to degree sequences for which an asymptotic evaluation of
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
is available in the literature. Without loss of generality we may assume that
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
is available in the literature. Without loss of generality we may assume that
![]() $d_1 \ge \cdots \ge d_n \ge 1$
. Let
$d_1 \ge \cdots \ge d_n \ge 1$
. Let
![]() $\Delta (\textbf{d}) = d_1$
and
$\Delta (\textbf{d}) = d_1$
and
![]() $\delta (\textbf{d}) = d_n$
. Another important parameter of
$\delta (\textbf{d}) = d_n$
. Another important parameter of
![]() $\textbf{d}$
is
$\textbf{d}$
is
![]() $J(\textbf{d})=\sum _{i=1}^{d_1} d_i$
. The following proposition, a direct corollary of [Reference Gao and Ohapkin20, Theorem 1], estimates the edge probabilities in
$J(\textbf{d})=\sum _{i=1}^{d_1} d_i$
. The following proposition, a direct corollary of [Reference Gao and Ohapkin20, Theorem 1], estimates the edge probabilities in
![]() ${\mathcal G}(n,\textbf{d})$
when
${\mathcal G}(n,\textbf{d})$
when
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
Proposition 1.3. (Corollary of [20, Theorem 1]) Suppose that
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
. Then
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
. Then
Remark 1.4. The condition
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
requires
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
requires
![]() $\textbf{d}$
to be a sparse degree sequence. It also restrict the tail of
$\textbf{d}$
to be a sparse degree sequence. It also restrict the tail of
![]() $\textbf{d}$
so that there cannot be too many degrees that are very large. See Proposition 3.2 in the Appendix for properties of
$\textbf{d}$
so that there cannot be too many degrees that are very large. See Proposition 3.2 in the Appendix for properties of
![]() $\textbf{d}$
that satisfies this technical condition. The edge probability in Proposition 1.3 is in general not correct without the condition
$\textbf{d}$
that satisfies this technical condition. The edge probability in Proposition 1.3 is in general not correct without the condition
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
. See an example like this in Remark 1.9.
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
. See an example like this in Remark 1.9.
Remark 1.5. Although Proposition 1.3 does not give asymptotic estimate of
![]() ${\mathbb P}(jk \in{\mathcal G}(n, \textbf{d}) )$
for every degree sequence, there are many interesting families of degree sequences satisfying
${\mathbb P}(jk \in{\mathcal G}(n, \textbf{d}) )$
for every degree sequence, there are many interesting families of degree sequences satisfying
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
, including examples of
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
, including examples of
-
• all
 $d$
-regular, and near-
$d$
-regular, and near-
 $d$
-regular degree sequences (namely, all degrees are asymptotic to
$d$
-regular degree sequences (namely, all degrees are asymptotic to
 $d$
) where
$d$
) where
 $d=o(n)$
;
$d=o(n)$
; -
• all perturbed sequences from a near-
 $d$
-regular degree sequence by arbitrarily decreasing at most
$d$
-regular degree sequence by arbitrarily decreasing at most
 $(1-c)n$
entries, where
$(1-c)n$
entries, where
 $c\gt 0$
is fixed, and
$c\gt 0$
is fixed, and
 $d=o(n)$
;
$d=o(n)$
; -
• heavy-tailed degree sequences such as power-law sequences. We refer interested readers to [22, Section 2] for a formal definition of power-law sequences and other examples of heavy-tailed degree sequences.
Assume that
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
. It is easy to show that for most pairs
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
. It is easy to show that for most pairs
![]() $jk$
,
$jk$
,
![]() $d_jd_k=o(\|\textbf{d}\|_1)$
(e.g. see Proposition 3.2 in the Appendix), and thus by Proposition 1.3 their edge probabilities are
$d_jd_k=o(\|\textbf{d}\|_1)$
(e.g. see Proposition 3.2 in the Appendix), and thus by Proposition 1.3 their edge probabilities are
![]() $o(1)$
. On the other hand, if there exist pairs
$o(1)$
. On the other hand, if there exist pairs
![]() $jk$
such that
$jk$
such that
![]() $d_jd_k=\Omega (\|\textbf{d}\|_1)$
, then Proposition 1.3 implies that the edge probabilities in
$d_jd_k=\Omega (\|\textbf{d}\|_1)$
, then Proposition 1.3 implies that the edge probabilities in
![]() ${\mathcal G}(n,\textbf{d})$
will not be uniformly
${\mathcal G}(n,\textbf{d})$
will not be uniformly
![]() $o(1)$
. In particular, for every such pair
$o(1)$
. In particular, for every such pair
![]() $jk$
the edge probability of
$jk$
the edge probability of
![]() $jk$
is bounded from below by some constant
$jk$
is bounded from below by some constant
![]() $c\gt 1$
. In fact, there exist degree sequences
$c\gt 1$
. In fact, there exist degree sequences
![]() $\textbf{d}$
satisfying
$\textbf{d}$
satisfying
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
whose edge probabilities takes values ranging from
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
whose edge probabilities takes values ranging from
![]() $o(1)$
to constant
$o(1)$
to constant
![]() $0\lt c\lt 1$
and to
$0\lt c\lt 1$
and to
![]() $1-o(1)$
. The power-law sequences mentioned in Remark 1.5 are good examples like this. As we will see later, it is the presence of such diverse edge probabilities that poses a challenge to embedding
$1-o(1)$
. The power-law sequences mentioned in Remark 1.5 are good examples like this. As we will see later, it is the presence of such diverse edge probabilities that poses a challenge to embedding
![]() ${\mathcal G}(n,W)$
into
${\mathcal G}(n,W)$
into
![]() ${\mathcal G}(n,\textbf{d})$
.
${\mathcal G}(n,\textbf{d})$
.
In light of Proposition 1.3, we define matrix
![]() $P(\textbf{d})$
, which is asymptotic to
$P(\textbf{d})$
, which is asymptotic to
![]() $W^*(\textbf{d})$
under the condition
$W^*(\textbf{d})$
under the condition
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
Definition 1.6.
Given
![]() $\textbf{d}=(d_1,\ldots, d_n)$
, let
$\textbf{d}=(d_1,\ldots, d_n)$
, let
![]() $P({\textbf{d}})$
be the symmetric
$P({\textbf{d}})$
be the symmetric
![]() $n\times n$
matrix defined by
$n\times n$
matrix defined by
![]() $P_{ij}=P_{ji}=\frac{d_id_j}{\|\textbf{d}\|_1+d_id_j}$
, for every
$P_{ij}=P_{ji}=\frac{d_id_j}{\|\textbf{d}\|_1+d_id_j}$
, for every
![]() $1\le i\lt j\le n$
, and
$1\le i\lt j\le n$
, and
![]() $P_{ii}=0$
for every
$P_{ii}=0$
for every
![]() $1\le i\le n$
.
$1\le i\le n$
.
One of our main results is the following theorem, which gives a positive answer to Question 1.2 for degree sequences satisfying
![]() $\Delta (\textbf{d})^2 = o(\|\textbf{d}\|_1)$
, a condition that is stronger than
$\Delta (\textbf{d})^2 = o(\|\textbf{d}\|_1)$
, a condition that is stronger than
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
Theorem 1.7.
Assume that
![]() $\textbf{d} = \textbf{d}(n)$
is a degree sequence satisfying
$\textbf{d} = \textbf{d}(n)$
is a degree sequence satisfying
![]() $\Delta (\textbf{d})^2 = o(\|\textbf{d}\|_1)$
and
$\Delta (\textbf{d})^2 = o(\|\textbf{d}\|_1)$
and
![]() $\delta (\textbf{d}) \gg \log{n}$
. Then, there exist
$\delta (\textbf{d}) \gg \log{n}$
. Then, there exist
![]() $\varepsilon =o(1)$
and a coupling
$\varepsilon =o(1)$
and a coupling
![]() $(G_L, G)$
, where
$(G_L, G)$
, where
![]() $G_L \sim{\mathcal G}(n, W)$
,
$G_L \sim{\mathcal G}(n, W)$
,
![]() $W=(1-\varepsilon )P(\textbf{d})$
, and
$W=(1-\varepsilon )P(\textbf{d})$
, and
![]() $G \sim{\mathcal G}(n, \textbf{d})$
, such that
$G \sim{\mathcal G}(n, \textbf{d})$
, such that
![]() ${\mathbb P}(G_L \subseteq G) = 1-o(1)$
.
${\mathbb P}(G_L \subseteq G) = 1-o(1)$
.
Under the stronger condition that
![]() $\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
,
$\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
,
![]() $d_jd_k=o(\|\textbf{d}\|_1)$
for all
$d_jd_k=o(\|\textbf{d}\|_1)$
for all
![]() $jk\in \binom{[n]}{2}$
, and thus
$jk\in \binom{[n]}{2}$
, and thus
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))=o(1)$
for all
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))=o(1)$
for all
![]() $jk\in \binom{[n]}{2}$
by Proposition 1.3. This property is a crucial element in our coupling scheme which allows us to achieve an optimal embedding. Our next theorem embeds
$jk\in \binom{[n]}{2}$
by Proposition 1.3. This property is a crucial element in our coupling scheme which allows us to achieve an optimal embedding. Our next theorem embeds
![]() ${\mathcal G}(n,W)$
into
${\mathcal G}(n,W)$
into
![]() ${\mathcal G}(n,\textbf{d})$
for
${\mathcal G}(n,\textbf{d})$
for
![]() $\textbf{d}$
satisfying
$\textbf{d}$
satisfying
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
. In this case,
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
. In this case,
![]() $W_{jk}=(1-o(1))P(\textbf{d})_{jk}$
for all
$W_{jk}=(1-o(1))P(\textbf{d})_{jk}$
for all
![]() $jk$
where
$jk$
where
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))=o(1)$
. However,
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))=o(1)$
. However,
![]() $W_{jk}$
is not asymptotic to
$W_{jk}$
is not asymptotic to
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
for
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
for
![]() $jk$
where
$jk$
where
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
is bounded away from 0. Given a function
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))$
is bounded away from 0. Given a function
![]() $f:{\mathbb R}\to{\mathbb R}$
, let
$f:{\mathbb R}\to{\mathbb R}$
, let
![]() $f(P)$
denote the matrix
$f(P)$
denote the matrix
![]() $(f(P_{i,j}))_{i,j\in [n]}$
.
$(f(P_{i,j}))_{i,j\in [n]}$
.
Theorem 1.8.
Assume that
![]() $\textbf{d}$
is a degree sequence satisfying
$\textbf{d}$
is a degree sequence satisfying
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
and
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
and
![]() $\delta (\textbf{d}) \gg \log{n}$
. Then, there exist
$\delta (\textbf{d}) \gg \log{n}$
. Then, there exist
![]() $\varepsilon =o(1)$
and a coupling
$\varepsilon =o(1)$
and a coupling
![]() $(G_L, G)$
, where
$(G_L, G)$
, where
![]() $G_L \sim{\mathcal G}(n, W)$
,
$G_L \sim{\mathcal G}(n, W)$
,
![]() $W=(1-\varepsilon )f(P(\textbf{d}))$
where
$W=(1-\varepsilon )f(P(\textbf{d}))$
where
![]() $f(x)=1-e^{-x}$
, and
$f(x)=1-e^{-x}$
, and
![]() $G \sim{\mathcal G}(n, \textbf{d})$
, such that
$G \sim{\mathcal G}(n, \textbf{d})$
, such that
![]() ${\mathbb P}(G_L \subseteq G) = 1-o(1)$
.
${\mathbb P}(G_L \subseteq G) = 1-o(1)$
.
We see that Theorem1.7 immediately follows from Theorem 1.8.
Proof of Theorem
1.7. Note that
![]() $\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
implies
$\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
implies
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
since
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
since
![]() $J(\textbf{d})\le \Delta (\textbf{d})^2$
. Moreover,
$J(\textbf{d})\le \Delta (\textbf{d})^2$
. Moreover,
![]() $\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
implies that
$\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
implies that
![]() $P({\textbf{d}})_{jk}=o(1)$
for all
$P({\textbf{d}})_{jk}=o(1)$
for all
![]() $jk$
by Definition 1.6. Now Theorem1.7 follows as a straightforward corollary of Theorem1.8 by noticing that
$jk$
by Definition 1.6. Now Theorem1.7 follows as a straightforward corollary of Theorem1.8 by noticing that
![]() $1-e^{-x}=(1+O(x))x$
.
$1-e^{-x}=(1+O(x))x$
.
Remark 1.9. Note that
![]() $P(\textbf{d})=(1+o(1))W^*(\textbf{d})$
is not true in general. For instance, consider the
$P(\textbf{d})=(1+o(1))W^*(\textbf{d})$
is not true in general. For instance, consider the
![]() $d$
-regular degree sequence where
$d$
-regular degree sequence where
![]() $d=\Theta (n)$
. By symmetry we know that
$d=\Theta (n)$
. By symmetry we know that
![]() $W^*_{jk}=d/(n-1)\sim d/n$
for every
$W^*_{jk}=d/(n-1)\sim d/n$
for every
![]() $jk$
. On the other hand, by Definition 1.6,
$jk$
. On the other hand, by Definition 1.6,
![]() $P_{jk}=d^2/(dn+d^2)=d/(n+d)$
which is not asymptotic to
$P_{jk}=d^2/(dn+d^2)=d/(n+d)$
which is not asymptotic to
![]() $d/n$
as
$d/n$
as
![]() $d=\Theta (n)$
. Thus, in this example,
$d=\Theta (n)$
. Thus, in this example,
![]() $P_{jk}$
is significantly smaller than
$P_{jk}$
is significantly smaller than
![]() $W^*_{jk}$
. There are two open problems below that can be very interesting for future research. The first question is a weaker version of Question 1.2, replacing
$W^*_{jk}$
. There are two open problems below that can be very interesting for future research. The first question is a weaker version of Question 1.2, replacing
![]() $W^*(\textbf{d})$
by
$W^*(\textbf{d})$
by
![]() $P(\textbf{d})$
.
$P(\textbf{d})$
.
-
(a) Does Theorem 1.8 hold with some
 $W=(1+o(1))P(\textbf{d})$
?
$W=(1+o(1))P(\textbf{d})$
?
Note that Theorem 1.7 answers the question above only for degree sequences satisfying
![]() $\Delta ^2=o(\|\textbf{d}\|_1)$
. However, in the more general setting as Theorem 1.8, there can be pairs
$\Delta ^2=o(\|\textbf{d}\|_1)$
. However, in the more general setting as Theorem 1.8, there can be pairs
![]() $jk$
where
$jk$
where
![]() $d_jd_k=\Omega (\|\textbf{d}\|_1)$
, and for such pairs, our current embedding requires
$d_jd_k=\Omega (\|\textbf{d}\|_1)$
, and for such pairs, our current embedding requires
![]() $W$
where
$W$
where
![]() $W_{jk}$
is significantly smaller than
$W_{jk}$
is significantly smaller than
![]() $P_{jk}$
. Hence we do not have a complete answer to question (a).
$P_{jk}$
. Hence we do not have a complete answer to question (a).
-
(b) Can Question 1.2 be answered for
 $\textbf{d}$
where
$\textbf{d}$
where
 $J(\textbf{d})=o(\|\textbf{d}\|_1)$
is not satisfied? In particular, is there a way to embed
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
is not satisfied? In particular, is there a way to embed
 ${\mathcal G}(n,W)$
into
${\mathcal G}(n,W)$
into
 ${\mathcal G}(n,\textbf{d})$
for some reasonable
${\mathcal G}(n,\textbf{d})$
for some reasonable
 $W$
without knowing the asymptotic value of
$W$
without knowing the asymptotic value of
 $W^*(\textbf{d})$
or the conditional edge probabilities as in Proposition 1.3?
$W^*(\textbf{d})$
or the conditional edge probabilities as in Proposition 1.3?
Remark 1.10. To obtain a sandwich-type result as for
![]() ${\mathcal G}(n,d)$
, we would hope to embed
${\mathcal G}(n,d)$
, we would hope to embed
![]() ${\mathcal G}(n,\textbf{d})$
into
${\mathcal G}(n,\textbf{d})$
into
![]() ${\mathcal G}(n, W)$
for some
${\mathcal G}(n, W)$
for some
![]() $W=(1+o(1))W^*$
. If we approach in the same way as for
$W=(1+o(1))W^*$
. If we approach in the same way as for
![]() ${\mathcal G}(n,d)$
, we would embed
${\mathcal G}(n,d)$
, we would embed
![]() ${\mathcal G}(n, (J-I)-(1+o(1))W^*)$
into
${\mathcal G}(n, (J-I)-(1+o(1))W^*)$
into
![]() ${\mathcal G}(n,(n-1)\textbf{1}-\textbf{d})$
where
${\mathcal G}(n,(n-1)\textbf{1}-\textbf{d})$
where
![]() $\textbf{1}$
is the all-one vector,
$\textbf{1}$
is the all-one vector,
![]() $J=\textbf{1}\textbf{1}^T$
and
$J=\textbf{1}\textbf{1}^T$
and
![]() $I$
is the identity matrix. Both the proofs in [17, 27] for embedding
$I$
is the identity matrix. Both the proofs in [17, 27] for embedding
![]() ${\mathcal G}(n,1-(1+o(1))d/n)$
into
${\mathcal G}(n,1-(1+o(1))d/n)$
into
![]() ${\mathcal G}(n,n-1-d)$
use some counting arguments that heavily rely on the fact that the underlying graphs (during the construction of the coupling) have almost equal degrees, and we do not think this argument can extend to graphs that are far away from being regular. In fact, we do not have enough intuition to support a sandwich conjecture for
${\mathcal G}(n,n-1-d)$
use some counting arguments that heavily rely on the fact that the underlying graphs (during the construction of the coupling) have almost equal degrees, and we do not think this argument can extend to graphs that are far away from being regular. In fact, we do not have enough intuition to support a sandwich conjecture for
![]() ${\mathcal G}(n,\textbf{d})$
as for
${\mathcal G}(n,\textbf{d})$
as for
![]() ${\mathcal G}(n,d)$
, especially for degree sequences
${\mathcal G}(n,d)$
, especially for degree sequences
![]() $\textbf{d}$
where the values of edge probabilities range from
$\textbf{d}$
where the values of edge probabilities range from
![]() $o(1)$
to
$o(1)$
to
![]() $1-o(1)$
.
$1-o(1)$
.
Throughout the paper
![]() $n$
is assumed to be sufficiently large. For two sequences of real numbers
$n$
is assumed to be sufficiently large. For two sequences of real numbers
![]() $(a_n)_{n=0}^{\infty }$
and
$(a_n)_{n=0}^{\infty }$
and
![]() $(b_n)_{n=0}^{\infty }$
, we write
$(b_n)_{n=0}^{\infty }$
, we write
![]() $a_n=O(b_n)$
if there is
$a_n=O(b_n)$
if there is
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $|a_n|\lt C|b_n|$
for every
$|a_n|\lt C|b_n|$
for every
![]() $n$
. We say
$n$
. We say
![]() $a_n=\Omega (b_n)$
if
$a_n=\Omega (b_n)$
if
![]() $a_n\gt 0$
and
$a_n\gt 0$
and
![]() $b_n=O(a_n)$
. We say
$b_n=O(a_n)$
. We say
![]() $b_n = o(a_n)$
, or
$b_n = o(a_n)$
, or
![]() $b_n \ll a_n$
, or
$b_n \ll a_n$
, or
![]() $a_n \gg b_n$
if
$a_n \gg b_n$
if
![]() $a_n\gt 0$
and
$a_n\gt 0$
and
![]() $\lim _{n \rightarrow \infty } b_n/a_n = 0$
. We say a sequence of events
$\lim _{n \rightarrow \infty } b_n/a_n = 0$
. We say a sequence of events
![]() $A_n$
indexed by
$A_n$
indexed by
![]() $n$
holds a.a.s. (asymptotically almost surely) if
$n$
holds a.a.s. (asymptotically almost surely) if
![]() ${\mathbb P}(A_n)=1-o(1)$
. All asymptotics are with respect to
${\mathbb P}(A_n)=1-o(1)$
. All asymptotics are with respect to
![]() $n \rightarrow \infty$
.
$n \rightarrow \infty$
.
1.1 Relation between
 $\mathcal{G}(n,P(\textbf{d}))$
and the Chung–Lu model
$\mathcal{G}(n,P(\textbf{d}))$
and the Chung–Lu model
In 2002, Chung and Lu introduced the random graph model with given expected degrees [Reference Chung and Lu9–Reference Chung, Lu and Vu12]. Given a sequence of nonnegative real numbers
![]() $\textbf{w}=(w_1,\ldots, w_n)$
satisfying that
$\textbf{w}=(w_1,\ldots, w_n)$
satisfying that
the random graph
![]() $G(\textbf{w})$
is defined by
$G(\textbf{w})$
is defined by
![]() ${\mathcal G}(n,\hat W(\textbf{w}))$
where
${\mathcal G}(n,\hat W(\textbf{w}))$
where
![]() $\hat W_{jk}(\textbf{w})=w_jw_k/\|\textbf{w}\|_1$
. To avoid relying on the assumption [1] one can define
$\hat W_{jk}(\textbf{w})=w_jw_k/\|\textbf{w}\|_1$
. To avoid relying on the assumption [1] one can define
![]() $\hat W_{jk}=\min \{w_jw_k/\|\textbf{w}\|_1,1\}$
. However, most of the work about the Chung–Lu model assumed [1]. Notice that the three matrices
$\hat W_{jk}=\min \{w_jw_k/\|\textbf{w}\|_1,1\}$
. However, most of the work about the Chung–Lu model assumed [1]. Notice that the three matrices
![]() $P(\textbf{d})$
,
$P(\textbf{d})$
,
![]() $W^*(\textbf{d})$
, and
$W^*(\textbf{d})$
, and
![]() $\hat W(\textbf{d})$
are all asymptotically equal if
$\hat W(\textbf{d})$
are all asymptotically equal if
![]() $\textbf{d}$
satisfies
$\textbf{d}$
satisfies
![]() $\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
, as under this assumption,
$\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
, as under this assumption,
![]() $P(\textbf{d})_{jk}\sim W^*(\textbf{d})_{jk}\sim \hat W(\textbf{d})_{jk}=d_jd_k/\|\textbf{d}\|_1$
for all
$P(\textbf{d})_{jk}\sim W^*(\textbf{d})_{jk}\sim \hat W(\textbf{d})_{jk}=d_jd_k/\|\textbf{d}\|_1$
for all
![]() $jk$
, by definition of these three matrices and Proposition 1.3. However, if there exists
$jk$
, by definition of these three matrices and Proposition 1.3. However, if there exists
![]() $jk$
such that
$jk$
such that
![]() $d_jd_k=\Omega (\|\textbf{d}\|_1)$
then
$d_jd_k=\Omega (\|\textbf{d}\|_1)$
then
![]() $P(\textbf{d})_{jk}$
,
$P(\textbf{d})_{jk}$
,
![]() $W^*(\textbf{d})_{jk}$
, and
$W^*(\textbf{d})_{jk}$
, and
![]() $\hat W(\textbf{d})_{jk}$
may be all asymptotically distinct.
$\hat W(\textbf{d})_{jk}$
may be all asymptotically distinct.
1.2 Applications
Given two
![]() $n\times n$
matrices
$n\times n$
matrices
![]() $W_1$
and
$W_1$
and
![]() $W_2$
, we say
$W_2$
, we say
![]() $W_1\le W_2$
if
$W_1\le W_2$
if
![]() $(W_1)_{ij}\le (W_2)_{ij}$
for every
$(W_1)_{ij}\le (W_2)_{ij}$
for every
![]() $i,j\in [n]$
. It is well known that
$i,j\in [n]$
. It is well known that
![]() ${\mathcal G}(n,W)$
has the nice “nesting property”, meaning that
${\mathcal G}(n,W)$
has the nice “nesting property”, meaning that
![]() ${\mathcal G}(n,W_1)$
can be embedded into
${\mathcal G}(n,W_1)$
can be embedded into
![]() ${\mathcal G}(n,W_2)$
provided that
${\mathcal G}(n,W_2)$
provided that
![]() $W_1\le W_2$
. However,
$W_1\le W_2$
. However,
![]() ${\mathcal G}(n,\textbf{d})$
does not have the nesting property. Given two degree sequences
${\mathcal G}(n,\textbf{d})$
does not have the nesting property. Given two degree sequences
![]() $\textbf{d}\preceq \textbf{g}$
, it is in general not true that
$\textbf{d}\preceq \textbf{g}$
, it is in general not true that
![]() ${\mathcal G}(n,\textbf{d})$
can be embedded into
${\mathcal G}(n,\textbf{d})$
can be embedded into
![]() ${\mathcal G}(n,\textbf{g})$
. In fact, it is easy to construct degree sequences
${\mathcal G}(n,\textbf{g})$
. In fact, it is easy to construct degree sequences
![]() $\textbf{d}\preceq \textbf{g}$
for which there exists
$\textbf{d}\preceq \textbf{g}$
for which there exists
![]() $jk$
such that
$jk$
such that
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))= 1-o(1)$
and
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))= 1-o(1)$
and
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{g}))=o(1)$
(see an example like this in the Appendix). Consequently and perhaps rather surprisingly, it is difficult to prove some rather “intuitive” results about
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{g}))=o(1)$
(see an example like this in the Appendix). Consequently and perhaps rather surprisingly, it is difficult to prove some rather “intuitive” results about
![]() ${\mathcal G}(n,\textbf{d})$
. For instance, although it is known that a.a.s.
${\mathcal G}(n,\textbf{d})$
. For instance, although it is known that a.a.s.
![]() ${\mathcal G}(n,3)$
is connected, to our knowledge it is not known if
${\mathcal G}(n,3)$
is connected, to our knowledge it is not known if
![]() ${\mathcal G}(n,\textbf{d})$
is a.a.s. connected for every
${\mathcal G}(n,\textbf{d})$
is a.a.s. connected for every
![]() $\textbf{d}$
provided that
$\textbf{d}$
provided that
![]() $\delta (\textbf{d})\ge 3$
[Reference Gao and Ohapkin20]. Most such results are restricted to certain families of degree sequences for which either some enumeration results are known, or some enumeration proof techniques can be applied. Theorem1.8 gives a powerful tool to obtain such results by first embedding
$\delta (\textbf{d})\ge 3$
[Reference Gao and Ohapkin20]. Most such results are restricted to certain families of degree sequences for which either some enumeration results are known, or some enumeration proof techniques can be applied. Theorem1.8 gives a powerful tool to obtain such results by first embedding
![]() ${\mathcal G}(n,W)$
into
${\mathcal G}(n,W)$
into
![]() ${\mathcal G}(n,\textbf{d})$
and then applying the nesting property of
${\mathcal G}(n,\textbf{d})$
and then applying the nesting property of
![]() ${\mathcal G}(n,W)$
. We show a few examples below.
${\mathcal G}(n,W)$
. We show a few examples below.
Theorem 1.11.
Assume
![]() $\textbf{d}$
is a degree sequence satisfying
$\textbf{d}$
is a degree sequence satisfying
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
and
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
and
![]() $\delta (\textbf{d}) \gg \log{n}$
. Then,
$\delta (\textbf{d}) \gg \log{n}$
. Then,
-
(a) if
 $\delta (\textbf{d})^2/\|\textbf{d}\|_1\ge (1+c)\log n/n$
for some fixed
$\delta (\textbf{d})^2/\|\textbf{d}\|_1\ge (1+c)\log n/n$
for some fixed
 $c\gt 0$
then a.a.s.
$c\gt 0$
then a.a.s.
 ${\mathcal G}(n,\textbf{d})$
is Hamiltonian and
${\mathcal G}(n,\textbf{d})$
is Hamiltonian and
 $k$
-connected for every fixed
$k$
-connected for every fixed
 $k$
;
$k$
; -
(b) if
 $\delta (\textbf{d})^2/\|\textbf{d}\|_1\ge c/n$
for some fixed
$\delta (\textbf{d})^2/\|\textbf{d}\|_1\ge c/n$
for some fixed
 $c\gt 1$
then a.a.s.
$c\gt 1$
then a.a.s.
 ${\mathcal G}(n,\textbf{d})$
contains
${\mathcal G}(n,\textbf{d})$
contains
 $H$
as a minor for every fixed graph
$H$
as a minor for every fixed graph
 $H$
;
$H$
; -
(c) if
 $\delta (\textbf{d})^2/\|\textbf{d}\|_1\ge n^{-2/(k+1)+c}$
for some fixed
$\delta (\textbf{d})^2/\|\textbf{d}\|_1\ge n^{-2/(k+1)+c}$
for some fixed
 $c\gt 0$
where
$c\gt 0$
where
 $k\gt 0$
is a fixed integer, then a.a.s. simultaneously for all graphs
$k\gt 0$
is a fixed integer, then a.a.s. simultaneously for all graphs
 $H$
on
$H$
on
 $[n]$
with maximum degree at most
$[n]$
with maximum degree at most
 $k$
,
$k$
,
 ${\mathcal G}(n,\textbf{d})$
has a subgraph isomorphic to
${\mathcal G}(n,\textbf{d})$
has a subgraph isomorphic to
 $H$
.
$H$
.
Proof. By definition,
![]() $P(\textbf{d})_{jk}\ge (1-o(1))\delta (\textbf{d})^2/\|\textbf{d}\|_1$
for every
$P(\textbf{d})_{jk}\ge (1-o(1))\delta (\textbf{d})^2/\|\textbf{d}\|_1$
for every
![]() $jk$
. Thus, by Theorem1.8 and the nesting property of
$jk$
. Thus, by Theorem1.8 and the nesting property of
![]() ${\mathcal G}(n,W)$
,
${\mathcal G}(n,W)$
,
![]() ${\mathcal G}(n,p)$
can be embedded into
${\mathcal G}(n,p)$
can be embedded into
![]() ${\mathcal G}(n,\textbf{d})$
for some
${\mathcal G}(n,\textbf{d})$
for some
![]() $p= (1-o(1))\delta (\textbf{d})^2/\|\textbf{d}\|_1$
. Parts (a,b) follow as for every fixed
$p= (1-o(1))\delta (\textbf{d})^2/\|\textbf{d}\|_1$
. Parts (a,b) follow as for every fixed
![]() $c\gt 0$
,
$c\gt 0$
,
![]() ${\mathcal G}(n,(1+c)\log n/n)$
is a.a.s. Hamiltonian and
${\mathcal G}(n,(1+c)\log n/n)$
is a.a.s. Hamiltonian and
![]() $k$
-connected [Reference Bollobás and Bollobás7]; and
$k$
-connected [Reference Bollobás and Bollobás7]; and
![]() ${\mathcal G}(n,c/n)$
contains every fixed graph minor when
${\mathcal G}(n,c/n)$
contains every fixed graph minor when
![]() $c\gt 1$
[Reference Fountoulakis, Kühn and Osthus15]. Part (c) follows from Theorem 7.2 of [Reference Frankston, Kahn, Narayanan and Park16].
$c\gt 1$
[Reference Fountoulakis, Kühn and Osthus15]. Part (c) follows from Theorem 7.2 of [Reference Frankston, Kahn, Narayanan and Park16].
Remark 1.12. It should be possible to improve or even remove some assumptions such as
![]() $\delta (\textbf{d})^2/\|\textbf{d}\|_1\ge (1+c)\log n/n$
for some fixed
$\delta (\textbf{d})^2/\|\textbf{d}\|_1\ge (1+c)\log n/n$
for some fixed
![]() $c\gt 0$
in part (a), by directly analysing
$c\gt 0$
in part (a), by directly analysing
![]() ${\mathcal G}(n, (1+o(1))f(P(\textbf{d})))$
. For instance, the sharp threshold of Hamiltonicity was studied for the stochastic block model [1]. We did not attempt it as the main objective of this paper is to prove the embedding theorems.
${\mathcal G}(n, (1+o(1))f(P(\textbf{d})))$
. For instance, the sharp threshold of Hamiltonicity was studied for the stochastic block model [1]. We did not attempt it as the main objective of this paper is to prove the embedding theorems.
2. The coupling procedure
2.1 The old and the new
Assume that we aim to embed
![]() ${\mathcal G}(n,p)$
into
${\mathcal G}(n,p)$
into
![]() ${\mathcal G}(n,d)$
where
${\mathcal G}(n,d)$
where
![]() $p=(1-o(1))d/n$
. Regardless of a few minor differences, the coupling procedures employed in [Reference Dudek, Frieze, Ruciński and Šileikis14, Reference Gao, Isaev and McKay17–Reference Gao, Isaev and McKay19, Reference Kim and Vu25, Reference Klimošová, Reiher, Ruciński and Šileikis26] all use the following approach, which was introduced in the original paper of Kim and Vu [Reference Kim and Vu25]: let
$p=(1-o(1))d/n$
. Regardless of a few minor differences, the coupling procedures employed in [Reference Dudek, Frieze, Ruciński and Šileikis14, Reference Gao, Isaev and McKay17–Reference Gao, Isaev and McKay19, Reference Kim and Vu25, Reference Klimošová, Reiher, Ruciński and Šileikis26] all use the following approach, which was introduced in the original paper of Kim and Vu [Reference Kim and Vu25]: let
![]() $x_1,x_2,\ldots, x_m$
be a sequence of random edges, each uniformly and independently chosen from
$x_1,x_2,\ldots, x_m$
be a sequence of random edges, each uniformly and independently chosen from
![]() $K_n$
(here
$K_n$
(here
![]() $m$
is a carefully chosen integer-valued random variable that is concentrated around
$m$
is a carefully chosen integer-valued random variable that is concentrated around
![]() $\|\textbf{d}\|_1/2$
). Sequentially add edges in this sequence to
$\|\textbf{d}\|_1/2$
). Sequentially add edges in this sequence to
![]() $G$
and to
$G$
and to
![]() $G_L$
, respectively. With a small probability
$G_L$
, respectively. With a small probability
![]() ${\epsilon }_i=o(1)$
, edge
${\epsilon }_i=o(1)$
, edge
![]() $x_i$
is rejected by
$x_i$
is rejected by
![]() $G$
; and with a slightly larger (than
$G$
; and with a slightly larger (than
![]() ${\epsilon }_i$
) but still rather small probability
${\epsilon }_i$
) but still rather small probability
![]() $\zeta$
,
$\zeta$
,
![]() $x_i$
is rejected by
$x_i$
is rejected by
![]() $G_L$
. The parameter
$G_L$
. The parameter
![]() ${\epsilon }_i$
is chosen to be proportional to
${\epsilon }_i$
is chosen to be proportional to
![]() $p_i(x_i)$
, the probability that
$p_i(x_i)$
, the probability that
![]() $x_i$
is an edge of
$x_i$
is an edge of
![]() ${\mathcal G}(n,\textbf{d})$
conditional on the event that all the edges that have been added to
${\mathcal G}(n,\textbf{d})$
conditional on the event that all the edges that have been added to
![]() $G$
are edges of
$G$
are edges of
![]() ${\mathcal G}(n,\textbf{d})$
. The key idea of the coupling procedure is that, until
${\mathcal G}(n,\textbf{d})$
. The key idea of the coupling procedure is that, until
![]() $m$
gets very close to
$m$
gets very close to
![]() $dn/2$
, with high probability,
$dn/2$
, with high probability,
![]() $p_i(jk)$
is approximately the same for every edge
$p_i(jk)$
is approximately the same for every edge
![]() $jk$
that has not been added to
$jk$
that has not been added to
![]() $G$
yet. Since
$G$
yet. Since
![]() $x_i$
is uniformly chosen, a small rejection probability
$x_i$
is uniformly chosen, a small rejection probability
![]() ${\epsilon }_i$
suffices to ensure that
${\epsilon }_i$
suffices to ensure that
![]() $x_i$
is added to
$x_i$
is added to
![]() $G$
according to the correct conditional probability. We can prove that with high probability,
$G$
according to the correct conditional probability. We can prove that with high probability,
![]() ${\epsilon }_i=o(1)$
for every
${\epsilon }_i=o(1)$
for every
![]() $1\le i\le m$
, where
$1\le i\le m$
, where
![]() $m$
, as commented earlier, is concentrated around
$m$
, as commented earlier, is concentrated around
![]() $(1-o(1))dn/2$
. Hence we can choose some
$(1-o(1))dn/2$
. Hence we can choose some
![]() $\zeta =o(1)$
such that
$\zeta =o(1)$
such that
![]() ${\epsilon }_i\le \zeta$
for every
${\epsilon }_i\le \zeta$
for every
![]() $1\le i\le m$
. Moreover, (a)
$1\le i\le m$
. Moreover, (a)
![]() $G_L$
obtained after the
$G_L$
obtained after the
![]() $m$
-th iteration is a uniformly random graph conditional on the number of edges it contains, as every edge in
$m$
-th iteration is a uniformly random graph conditional on the number of edges it contains, as every edge in
![]() $\binom{[n]}{2}$
has an equal probability to be added to
$\binom{[n]}{2}$
has an equal probability to be added to
![]() $G_L$
; and (b)
$G_L$
; and (b)
![]() $G_L$
is a subgraph of
$G_L$
is a subgraph of
![]() $G$
, as the rejection probability
$G$
, as the rejection probability
![]() $\zeta$
for
$\zeta$
for
![]() $G_L$
is slightly larger than that for
$G_L$
is slightly larger than that for
![]() $G$
in every step.
$G$
in every step.
Now we are considering
![]() $\textbf{d}$
where the degrees are not all asymptotically the same. The most natural way to extend the previous coupling procedure is to generate the sequence of i.i.d. random edges
$\textbf{d}$
where the degrees are not all asymptotically the same. The most natural way to extend the previous coupling procedure is to generate the sequence of i.i.d. random edges
![]() $x_1,x_2,\ldots, x_m$
where each edge is chosen with probability proportional to
$x_1,x_2,\ldots, x_m$
where each edge is chosen with probability proportional to
![]() $W^*(\textbf{d})$
. This coupling procedure works well when
$W^*(\textbf{d})$
. This coupling procedure works well when
![]() $\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
. This is because the conditional probability
$\Delta (\textbf{d})^2=o(\|\textbf{d}\|_1)$
. This is because the conditional probability
![]() $p_i(jk)$
of
$p_i(jk)$
of
![]() $jk$
being an edge of
$jk$
being an edge of
![]() ${\mathcal G}(n,\textbf{d})$
in step
${\mathcal G}(n,\textbf{d})$
in step
![]() $i$
of the procedure turns out to be proportional to
$i$
of the procedure turns out to be proportional to
![]() $W^*(\textbf{d})_{jk}$
uniformly for all
$W^*(\textbf{d})_{jk}$
uniformly for all
![]() $jk$
during the whole coupling process, resulting a small rejection probability
$jk$
during the whole coupling process, resulting a small rejection probability
![]() ${\epsilon }_i$
. However, rather surprisingly, if there exists
${\epsilon }_i$
. However, rather surprisingly, if there exists
![]() $jk$
such that
$jk$
such that
![]() $d_jd_k=\Omega (\|\textbf{d}\|_1)$
then the ratio
$d_jd_k=\Omega (\|\textbf{d}\|_1)$
then the ratio
![]() $p_i(jk)/W^*_{jk}$
changes in a non-uniform way over
$p_i(jk)/W^*_{jk}$
changes in a non-uniform way over
![]() $jk$
and over time
$jk$
and over time
![]() $i$
of the coupling procedure, resulting larger and larger rejection probability
$i$
of the coupling procedure, resulting larger and larger rejection probability
![]() ${\epsilon }_i$
. As
${\epsilon }_i$
. As
![]() $\zeta$
has to be chosen uniformly during the process, we can only choose
$\zeta$
has to be chosen uniformly during the process, we can only choose
![]() $\zeta =1-o(1)$
, meaning that almost all edges are rejected by
$\zeta =1-o(1)$
, meaning that almost all edges are rejected by
![]() $G_L$
. The coupling procedure thus fails.
$G_L$
. The coupling procedure thus fails.
To overcome the challenges, we develop two novel ideas.
-
• Instead of using the same rejection probability
 $\zeta$
for every edge to be added to
$\zeta$
for every edge to be added to
 $G_L$
, we use different rejection probabilities for different edges. However, for a given edge
$G_L$
, we use different rejection probabilities for different edges. However, for a given edge
 $jk$
, the rejection probability
$jk$
, the rejection probability
 $\zeta _{jk}$
remains uniform throughout the procedure. This uniformity is needed for the output
$\zeta _{jk}$
remains uniform throughout the procedure. This uniformity is needed for the output
 $G_L$
to have the correct distribution.
$G_L$
to have the correct distribution. -
• During the coupling procedure, the value of
 $p_i(jk)/W^*_{jk}$
decreases significantly for edges
$p_i(jk)/W^*_{jk}$
decreases significantly for edges
 $jk$
where
$jk$
where
 $d_jd_k=O(\|\textbf{d}\|_1)$
, but changes little for
$d_jd_k=O(\|\textbf{d}\|_1)$
, but changes little for
 $jk$
where
$jk$
where
 $d_jd_k\gg \|\textbf{d}\|_1$
. Consequently, many rejections (particularly those where
$d_jd_k\gg \|\textbf{d}\|_1$
. Consequently, many rejections (particularly those where
 $d_jd_k\ll \|\textbf{d}\|_1$
) occur already for the construction of
$d_jd_k\ll \|\textbf{d}\|_1$
) occur already for the construction of
 $G$
, and thus the first idea above would not help, as even more rejections would occur for
$G$
, and thus the first idea above would not help, as even more rejections would occur for
 $G_L$
than for
$G_L$
than for
 $G$
. To reduce the rejection probability for the construction of
$G$
. To reduce the rejection probability for the construction of
 $G$
, we “intentionally” boost the probability (by an
$G$
, we “intentionally” boost the probability (by an
 $\omega (1)$
factor) of generating edges
$\omega (1)$
factor) of generating edges
 $jk$
where
$jk$
where
 $d_jd_k\gg \|\textbf{d}\|_1$
in the sequence of random edges
$d_jd_k\gg \|\textbf{d}\|_1$
in the sequence of random edges
 $x_1,x_2,\ldots$
. This probability boosting strategy magically reduces the rejection probability
$x_1,x_2,\ldots$
. This probability boosting strategy magically reduces the rejection probability
 ${\epsilon }_i(jk)$
for
${\epsilon }_i(jk)$
for
 $jk$
such that
$jk$
such that
 $d_jd_k\ll \|\textbf{d}\|_1$
(note that most
$d_jd_k\ll \|\textbf{d}\|_1$
(note that most
 $jk\in \binom{[n]}{2}$
are this type; see Proposition 3.2 in the Appendix). However, the rejection probabilities
$jk\in \binom{[n]}{2}$
are this type; see Proposition 3.2 in the Appendix). However, the rejection probabilities
 ${\epsilon }_i(jk)$
will be high (close to 1) for
${\epsilon }_i(jk)$
will be high (close to 1) for
 $jk$
where
$jk$
where
 $d_jd_k \gg \|\textbf{d}\|_1$
. Nonetheless, the first idea mentioned earlier will be applicable in this case — we reject these
$d_jd_k \gg \|\textbf{d}\|_1$
. Nonetheless, the first idea mentioned earlier will be applicable in this case — we reject these
 $jk$
more often than the others for the construction of
$jk$
more often than the others for the construction of
 $G_L$
. Consequently, the edge probability for such
$G_L$
. Consequently, the edge probability for such
 $jk$
in the final construction of
$jk$
in the final construction of
 $G_L$
turns out to be close to
$G_L$
turns out to be close to
 $1-e^{-1}$
instead of
$1-e^{-1}$
instead of
 $1$
. Note that for pairs
$1$
. Note that for pairs
 $jk$
where
$jk$
where
 $d_jd_k \gg \|\textbf{d}\|_1$
, their edge probability
$d_jd_k \gg \|\textbf{d}\|_1$
, their edge probability
 $W^*_{jk}$
in
$W^*_{jk}$
in
 ${\mathcal G}(n,\textbf{d})$
is asymptotic to 1 by Proposition 1.3. Thus, their edge probabilities in
${\mathcal G}(n,\textbf{d})$
is asymptotic to 1 by Proposition 1.3. Thus, their edge probabilities in
 $G_L$
(which is asymptotic to
$G_L$
(which is asymptotic to
 $1-e^{-1}$
) is smaller than
$1-e^{-1}$
) is smaller than
 $W^*_{jk}$
, implying that our embedding is not “tight”. The good news is that only a small proportion of
$W^*_{jk}$
, implying that our embedding is not “tight”. The good news is that only a small proportion of
 $jk\in \binom{[n]}{2}$
are of this type.
$jk\in \binom{[n]}{2}$
are of this type.
We define the procedure for sequential generation of
![]() ${\mathcal G}(n,W)$
in Section 2.2, the procedure for sequential generation of
${\mathcal G}(n,W)$
in Section 2.2, the procedure for sequential generation of
![]() ${\mathcal G}(n,\textbf{d})$
in Section 2.3. In Section 2.4 we couple the two procedures together to sequentially generate the coupled pair
${\mathcal G}(n,\textbf{d})$
in Section 2.3. In Section 2.4 we couple the two procedures together to sequentially generate the coupled pair
![]() $(G_L,G)$
. The parameters used by the coupling procedure will be specified in Section 2.5. Finally the proof of Theorem1.8 is given in Section 3.
$(G_L,G)$
. The parameters used by the coupling procedure will be specified in Section 2.5. Finally the proof of Theorem1.8 is given in Section 3.
2.2 Sequential generation of
 ${\mathcal G}(n,W)$
${\mathcal G}(n,W)$
We define a sequential sampling procedure SeqApprox-P(
![]() $\textbf{d},\lambda, \Lambda$
), which adds a sequence of edges one at a time, and outputs a random graph where every edge in
$\textbf{d},\lambda, \Lambda$
), which adds a sequence of edges one at a time, and outputs a random graph where every edge in
![]() $\binom{[n]}{2}$
appears independently. The input
$\binom{[n]}{2}$
appears independently. The input
![]() $\lambda$
is a positive real number, and
$\lambda$
is a positive real number, and
![]() $\Lambda \in [0,1]^{[n]\times [n]}$
is a symmetric
$\Lambda \in [0,1]^{[n]\times [n]}$
is a symmetric
![]() $n\times n$
matrix. We may think of
$n\times n$
matrix. We may think of
![]() $\textbf{d}$
as the target degree sequence. As mentioned before, instead of weighting edge probabilities according to their true probabilities in
$\textbf{d}$
as the target degree sequence. As mentioned before, instead of weighting edge probabilities according to their true probabilities in
![]() ${\mathcal G}(n,\textbf{d})$
, we boost the probability of edge
${\mathcal G}(n,\textbf{d})$
, we boost the probability of edge
![]() $jk$
if
$jk$
if
![]() $d_jd_k$
is large. To formalise this notion, we define matrix
$d_jd_k$
is large. To formalise this notion, we define matrix
![]() $Q$
as follows, which provides the probability distribution for the edges to be sequentially sampled in the procedure SeqApprox-P(
$Q$
as follows, which provides the probability distribution for the edges to be sequentially sampled in the procedure SeqApprox-P(
![]() $\textbf{d},\lambda, \Lambda$
).
$\textbf{d},\lambda, \Lambda$
).
Definition 2.1.
Given
![]() $\textbf{d}=(d_1,\ldots, d_n)$
, let
$\textbf{d}=(d_1,\ldots, d_n)$
, let
![]() $Q({\textbf{d}})$
be the symmetric
$Q({\textbf{d}})$
be the symmetric
![]() $n\times n$
matrix defined by
$n\times n$
matrix defined by
![]() $Q_{ij}=Q_{ji}=(\sum _{1\le k\lt \ell \le n}d_kd_\ell )^{-1}d_id_j$
, for every
$Q_{ij}=Q_{ji}=(\sum _{1\le k\lt \ell \le n}d_kd_\ell )^{-1}d_id_j$
, for every
![]() $1\le i\lt j\le n$
, and
$1\le i\lt j\le n$
, and
![]() $Q_{ii}=0$
for every
$Q_{ii}=0$
for every
![]() $1\le i\le n$
.
$1\le i\le n$
.
Procedure SeqApprox-P(
![]() $\textbf{d},\lambda, \Lambda$
) is given below. We use
$\textbf{d},\lambda, \Lambda$
) is given below. We use
![]() ${\textbf{Po}}(\lambda )$
to denote the Poisson distribution with mean
${\textbf{Po}}(\lambda )$
to denote the Poisson distribution with mean
![]() $\lambda$
.
$\lambda$
.

The parameters
![]() $\lambda$
and
$\lambda$
and
![]() $\Lambda$
will be set in Section 2.5. Roughly speaking,
$\Lambda$
will be set in Section 2.5. Roughly speaking,
![]() $\lambda$
is approximately
$\lambda$
is approximately
![]() $\|\textbf{d}\|_1/2$
so that the number of edges in the output of SeqApprox-P(
$\|\textbf{d}\|_1/2$
so that the number of edges in the output of SeqApprox-P(
![]() $\textbf{d},\lambda, \Lambda$
) is close to the number of edges in
$\textbf{d},\lambda, \Lambda$
) is close to the number of edges in
![]() ${\mathcal G}(n,\textbf{d})$
, if only a small proportion of them are to be rejected, which we will prove later. The matrix
${\mathcal G}(n,\textbf{d})$
, if only a small proportion of them are to be rejected, which we will prove later. The matrix
![]() $\Lambda$
is chosen so that
$\Lambda$
is chosen so that
![]() $\Lambda _{jk}$
is approximately
$\Lambda _{jk}$
is approximately
![]() $\|\textbf{d}\|_1/(d_jd_k+\|\textbf{d}\|_1)$
. Since each edge
$\|\textbf{d}\|_1/(d_jd_k+\|\textbf{d}\|_1)$
. Since each edge
![]() $jk$
is selected with probability proportional to
$jk$
is selected with probability proportional to
![]() $d_jd_k$
by the definition of
$d_jd_k$
by the definition of
![]() $Q$
, and due to the choice of
$Q$
, and due to the choice of
![]() $\Lambda$
, edge
$\Lambda$
, edge
![]() $jk$
is selected and accepted with probability proportional to
$jk$
is selected and accepted with probability proportional to
![]() $d_jd_k/(d_jd_k+\|\textbf{d}\|_1)$
, which is approximately
$d_jd_k/(d_jd_k+\|\textbf{d}\|_1)$
, which is approximately
![]() $W^*_{jk}$
as desired. The exact values of
$W^*_{jk}$
as desired. The exact values of
![]() $\lambda$
and
$\lambda$
and
![]() $\Lambda$
are only important when we couple the two sampling processes together. At this point, regardless of their values, we prove that the output of SeqApprox-P(
$\Lambda$
are only important when we couple the two sampling processes together. At this point, regardless of their values, we prove that the output of SeqApprox-P(
![]() $\textbf{d},\lambda, \Lambda$
) has distribution
$\textbf{d},\lambda, \Lambda$
) has distribution
![]() ${\mathcal G}(n,W)$
for some
${\mathcal G}(n,W)$
for some
![]() $W$
as a function of
$W$
as a function of
![]() $\textbf{d},\lambda$
and
$\textbf{d},\lambda$
and
![]() $\Lambda$
. For two matrices
$\Lambda$
. For two matrices
![]() $A$
and
$A$
and
![]() $B$
of the same dimension, we denote by
$B$
of the same dimension, we denote by
![]() $A\odot B$
the Hadamard product of
$A\odot B$
the Hadamard product of
![]() $A$
and
$A$
and
![]() $B$
, defined by
$B$
, defined by
![]() $(A\odot B)_{ij}= A_{ij} B_{ij}$
for every entry
$(A\odot B)_{ij}= A_{ij} B_{ij}$
for every entry
![]() $ij$
.
$ij$
.
Lemma 2.2.
SeqApprox-P(
![]() $\textbf{d},\lambda, \Lambda$
) returns a random graph
$\textbf{d},\lambda, \Lambda$
) returns a random graph
![]() $G$
with distribution
$G$
with distribution
![]() ${\mathcal G}(n,f(\Lambda \odot Q))$
, where
${\mathcal G}(n,f(\Lambda \odot Q))$
, where
![]() $Q=Q(\textbf{d})$
and
$Q=Q(\textbf{d})$
and
![]() $f(x)=1-\exp (-\lambda x)$
.
$f(x)=1-\exp (-\lambda x)$
.
Proof. Let
![]() $e_1 = j_1k_1, \dots, e_N = j_Nk_N$
be an enumeration of the edges in
$e_1 = j_1k_1, \dots, e_N = j_Nk_N$
be an enumeration of the edges in
![]() $\binom{[n]}{2}$
, where
$\binom{[n]}{2}$
, where
![]() $N = \binom{n}{2}$
. For
$N = \binom{n}{2}$
. For
![]() $1 \le i \le N$
, let
$1 \le i \le N$
, let
![]() $X_i$
denote the number of times that edge
$X_i$
denote the number of times that edge
![]() $e_i$
is sampled throughout SeqApprox-P(
$e_i$
is sampled throughout SeqApprox-P(
![]() $\textbf{d},\lambda, \Lambda$
). We prove that the components of
$\textbf{d},\lambda, \Lambda$
). We prove that the components of
![]() $\textbf{X}=(X_1,\ldots, X_N)$
are mutually independent, and consequently, every edge
$\textbf{X}=(X_1,\ldots, X_N)$
are mutually independent, and consequently, every edge
![]() $e_i$
appears independently in
$e_i$
appears independently in
![]() $G$
with probability
$G$
with probability
![]() ${\mathbb P}(X_i\ge 1)$
. For each edge
${\mathbb P}(X_i\ge 1)$
. For each edge
![]() $e_i\in \binom{[n]}{2}$
, the probability that
$e_i\in \binom{[n]}{2}$
, the probability that
![]() $e_i$
is in
$e_i$
is in
![]() $G$
is thus given by
$G$
is thus given by
 \begin{align*}{\mathbb P}(X_i \ge 1) &= 1-{\mathbb P}(X_i=0) =1-\sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} \sum _{j=0}^{m} \binom{m}{j} Q_{e_i}^j (1-Q_{e_i})^{m-j} \left (1-\Lambda _{e_i}\right )^j \\ & =1- \sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} (1- Q_{e_i}+Q_{e_i}(1-\Lambda _{e_i}))^m \\ &= 1- \exp \left (-\lambda +\lambda (1- Q_{e_i}+Q_{e_i}(1-\Lambda _{e_i}))\right )= 1-\exp (-\lambda Q_{e_i}\Lambda _{e_i}), \end{align*}
\begin{align*}{\mathbb P}(X_i \ge 1) &= 1-{\mathbb P}(X_i=0) =1-\sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} \sum _{j=0}^{m} \binom{m}{j} Q_{e_i}^j (1-Q_{e_i})^{m-j} \left (1-\Lambda _{e_i}\right )^j \\ & =1- \sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} (1- Q_{e_i}+Q_{e_i}(1-\Lambda _{e_i}))^m \\ &= 1- \exp \left (-\lambda +\lambda (1- Q_{e_i}+Q_{e_i}(1-\Lambda _{e_i}))\right )= 1-\exp (-\lambda Q_{e_i}\Lambda _{e_i}), \end{align*}
and the probability generating function for
![]() $X_i$
is given by
$X_i$
is given by
 \begin{align*}{\mathbb E} z^{X_i} &=\sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!}\sum _{j=0}^{m} \binom{m}{j} Q_{e_i}^j (1-Q_{e_i})^{m-j} \sum _{k=0}^j \binom{j}{i} \Lambda _{e_i}^k (1-\Lambda _{e_i})^{j-k} z^k \\ &=\sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} \sum _{j=0}^{m} \binom{m}{j} Q_{e_i}^j (1-Q_{e_i})^{m-j} (1-\Lambda _{e_i}+\Lambda _{e_i}z)^j\\ & =\sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} (1-Q_{e_i}+Q_{e_i}(1-\Lambda _{e_i}+\Lambda _{e_i}z))^m=\exp (-\lambda Q_{e_i}\Lambda _{e_i}(1-z)). \end{align*}
\begin{align*}{\mathbb E} z^{X_i} &=\sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!}\sum _{j=0}^{m} \binom{m}{j} Q_{e_i}^j (1-Q_{e_i})^{m-j} \sum _{k=0}^j \binom{j}{i} \Lambda _{e_i}^k (1-\Lambda _{e_i})^{j-k} z^k \\ &=\sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} \sum _{j=0}^{m} \binom{m}{j} Q_{e_i}^j (1-Q_{e_i})^{m-j} (1-\Lambda _{e_i}+\Lambda _{e_i}z)^j\\ & =\sum _{m=0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} (1-Q_{e_i}+Q_{e_i}(1-\Lambda _{e_i}+\Lambda _{e_i}z))^m=\exp (-\lambda Q_{e_i}\Lambda _{e_i}(1-z)). \end{align*}
On the other hand, the probability generating function for the random vector
![]() $\textbf{X}$
is given by
$\textbf{X}$
is given by
 \begin{align*} &\sum _{j_1, \dots, j_N}{\mathbb P}(X_1 = j_1, \dots, X_N = j_N) z_1^{j_1}\cdots z_N^{j_N} = \sum _{m = 0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} \left ( \sum \limits _{i=1}^{N} \big ( Q_{e_i} \Lambda _{e_i} z_i +Q_{e_i}(1-\Lambda _{e_i})\big ) \right )^m\\ &\hspace{1cm}= e^{-\lambda } \exp \left (\sum _{i=1}^N \big (\lambda Q_{e_i}\Lambda _{e_i}z_i +\lambda Q_{e_i}(1-\Lambda _{e_i}) \big )\right ) \\ & \qquad = \prod _{i=1}^N \exp \left (-\lambda \ Q_{e_i} \Lambda _{e_i}+\lambda Q_{e_i} \Lambda _{e_i} z_i\right )= \prod _{i=1}^N{\mathbb E} z^{X_i}, \end{align*}
\begin{align*} &\sum _{j_1, \dots, j_N}{\mathbb P}(X_1 = j_1, \dots, X_N = j_N) z_1^{j_1}\cdots z_N^{j_N} = \sum _{m = 0}^{\infty } e^{-\lambda } \frac{\lambda ^m}{m!} \left ( \sum \limits _{i=1}^{N} \big ( Q_{e_i} \Lambda _{e_i} z_i +Q_{e_i}(1-\Lambda _{e_i})\big ) \right )^m\\ &\hspace{1cm}= e^{-\lambda } \exp \left (\sum _{i=1}^N \big (\lambda Q_{e_i}\Lambda _{e_i}z_i +\lambda Q_{e_i}(1-\Lambda _{e_i}) \big )\right ) \\ & \qquad = \prod _{i=1}^N \exp \left (-\lambda \ Q_{e_i} \Lambda _{e_i}+\lambda Q_{e_i} \Lambda _{e_i} z_i\right )= \prod _{i=1}^N{\mathbb E} z^{X_i}, \end{align*}
where the second last equation above holds because
![]() $\sum _{i=1}^N Q_{e_i}=1$
by definition of
$\sum _{i=1}^N Q_{e_i}=1$
by definition of
![]() $Q$
. Hence we have shown that the components of
$Q$
. Hence we have shown that the components of
![]() $\textbf{X}$
are mutually independent. Thus,
$\textbf{X}$
are mutually independent. Thus,
![]() $G\sim{\mathcal G}(n,W)$
where
$G\sim{\mathcal G}(n,W)$
where
![]() $W$
is the symmetric
$W$
is the symmetric
![]() $n\times n$
matrix given by
$n\times n$
matrix given by
![]() $W_{ij}=1-\exp (-\lambda Q_{ij}\Lambda _{ij})$
for every
$W_{ij}=1-\exp (-\lambda Q_{ij}\Lambda _{ij})$
for every
![]() $i,j\in [n]$
.
$i,j\in [n]$
.
2.3 Sequential generation of
 ${\mathcal G}(n,\textbf{d})$
${\mathcal G}(n,\textbf{d})$
We define procedure SeqSample-D(
![]() $\textbf{d}$
) which sequentially generates a random graph with distribution
$\textbf{d}$
) which sequentially generates a random graph with distribution
![]() ${\mathcal G}(n,\textbf{d})$
. This procedure is essentially the same as previously used in [Reference Gao, Isaev and McKay17–Reference Gao, Isaev and McKay19, Reference Klimošová, Reiher, Ruciński and Šileikis26]. Let
${\mathcal G}(n,\textbf{d})$
. This procedure is essentially the same as previously used in [Reference Gao, Isaev and McKay17–Reference Gao, Isaev and McKay19, Reference Klimošová, Reiher, Ruciński and Šileikis26]. Let
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d})\mid H)$
denotes the probability that
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d})\mid H)$
denotes the probability that
![]() $jk$
is an edge of
$jk$
is an edge of
![]() ${\mathcal G}(n,\textbf{d})$
conditional on
${\mathcal G}(n,\textbf{d})$
conditional on
![]() $H$
being a subgraph of
$H$
being a subgraph of
![]() ${\mathcal G}(n,\textbf{d})$
.
${\mathcal G}(n,\textbf{d})$
.

Given
![]() $\textbf{d}$
, and an integer
$\textbf{d}$
, and an integer
![]() $0\le m\le \|\textbf{d}\|_1/2$
, let
$0\le m\le \|\textbf{d}\|_1/2$
, let
![]() ${\mathcal G}(n,\textbf{d},m)$
denote a uniformly random subgraph of
${\mathcal G}(n,\textbf{d},m)$
denote a uniformly random subgraph of
![]() ${\mathcal G}(n,\textbf{d})$
with exactly
${\mathcal G}(n,\textbf{d})$
with exactly
![]() $m$
edges. The following lemma follows by a simple counting argument and was proved in [Reference Gao, Isaev and McKay18, Lemma 3].
$m$
edges. The following lemma follows by a simple counting argument and was proved in [Reference Gao, Isaev and McKay18, Lemma 3].
Lemma 2.3.
Let
![]() $0\le m \le \|\textbf{d}\|_1/2$
and
$0\le m \le \|\textbf{d}\|_1/2$
and
![]() $G_m$
be the graph obtained after
$G_m$
be the graph obtained after
![]() $m$
iterations of SeqSample-D(
$m$
iterations of SeqSample-D(
![]() $\textbf{d}$
). Then
$\textbf{d}$
). Then
![]() $G_m\sim{\mathcal G}(n,\textbf{d},m)$
.
$G_m\sim{\mathcal G}(n,\textbf{d},m)$
.
Lemma 2.3 (with
![]() $m=\|\textbf{d}\|_1/2$
) immediately implies the following corollary.
$m=\|\textbf{d}\|_1/2$
) immediately implies the following corollary.
Corollary 2.4.
Let
![]() $G$
be the output of
$G$
be the output of
![]() ${\mathrm{\scriptsize SeqSample-D}}(\textbf{d})$
. Then
${\mathrm{\scriptsize SeqSample-D}}(\textbf{d})$
. Then
![]() $G \sim{\mathcal G}(n, \textbf{d})$
.
$G \sim{\mathcal G}(n, \textbf{d})$
.
We need the following lemma, which follows by standard concentration results and can be found in [Reference Gao, Isaev and McKay18, Lemma 4]. We use
![]() ${\textbf{Bin}}(K, p)$
to denote the Binomial distribution with
${\textbf{Bin}}(K, p)$
to denote the Binomial distribution with
![]() $K$
trials and success probability
$K$
trials and success probability
![]() $p$
. (Note that Lemma 4(c) of [Reference Gao, Isaev and McKay18] only states the upper tail bound of part (c) below; but its proof gives both the upper and lower tail bounds.)
$p$
. (Note that Lemma 4(c) of [Reference Gao, Isaev and McKay18] only states the upper tail bound of part (c) below; but its proof gives both the upper and lower tail bounds.)
Lemma 2.5.
Let
![]() $Y \sim{\textbf{Bin}}(K, p)$
for some positive integer
$Y \sim{\textbf{Bin}}(K, p)$
for some positive integer
![]() $K$
and
$K$
and
![]() $p \in [0, 1]$
.
$p \in [0, 1]$
.
-
(a) For any
 ${\epsilon }\ge 0$
,
${\epsilon }\ge 0$
,
 ${\mathbb P}(|Y- p K| \gt{\epsilon } p K) \le 2e^{-\frac{{\epsilon }^2}{2+{\epsilon }} pK}$
.
${\mathbb P}(|Y- p K| \gt{\epsilon } p K) \le 2e^{-\frac{{\epsilon }^2}{2+{\epsilon }} pK}$
. -
(b) If
 $p = j/K$
for some integer
$p = j/K$
for some integer
 $j \in (0, K)$
, then
$j \in (0, K)$
, then
 ${\mathbb P}(Y = j) \ge \frac{1}{3} (p(1-p) K)^{-1/2}$
.
${\mathbb P}(Y = j) \ge \frac{1}{3} (p(1-p) K)^{-1/2}$
. -
(c) Let
 ${\mathcal I}\sim{\textbf{Po}}(\mu )$
for some
${\mathcal I}\sim{\textbf{Po}}(\mu )$
for some
 $\mu \gt 0$
. Then, for any
$\mu \gt 0$
. Then, for any
 ${\epsilon }\ge 0$
,
${\epsilon }\ge 0$
,
 ${\mathbb P}(|{\mathcal I} -\mu |\ge{\epsilon }\mu )\le 2e^{-\frac{{\epsilon }^2}{2+{\epsilon }}\mu }$
.
${\mathbb P}(|{\mathcal I} -\mu |\ge{\epsilon }\mu )\le 2e^{-\frac{{\epsilon }^2}{2+{\epsilon }}\mu }$
.
The following lemma is similar to [Reference Gao, Isaev and McKay18, Lemma 6], whose proof easily extends to more general degree sequences
![]() $\textbf{d}$
discussed in this paper through straightforward adjustments. We include a short proof here. We will use this lemma to gain information on the remaining degree sequence of
$\textbf{d}$
discussed in this paper through straightforward adjustments. We include a short proof here. We will use this lemma to gain information on the remaining degree sequence of
![]() ${\mathcal G}(n,\textbf{d})$
when part of it has been constructed. Note that the probability lower bound
${\mathcal G}(n,\textbf{d})$
when part of it has been constructed. Note that the probability lower bound
![]() $1-\exp \left (-\Omega (\xi ^2 p_m d_j)+2\log n\right )$
below is not necessarily nonnegative. If it is negative then the assertion is trivially true.
$1-\exp \left (-\Omega (\xi ^2 p_m d_j)+2\log n\right )$
below is not necessarily nonnegative. If it is negative then the assertion is trivially true.
Lemma 2.6.
Let
![]() $0\le m\lt \|\textbf{d}\|_1/2$
and
$0\le m\lt \|\textbf{d}\|_1/2$
and
![]() $p_m = (\|\textbf{d}\|_1-2m)/\|\textbf{d}\|_1$
. Let
$p_m = (\|\textbf{d}\|_1-2m)/\|\textbf{d}\|_1$
. Let
![]() $d_j^{G_m}$
denote the degree of
$d_j^{G_m}$
denote the degree of
![]() $j$
in
$j$
in
![]() $G_m$
. For any
$G_m$
. For any
![]() $\xi =\xi _n\in (0,1)$
,
$\xi =\xi _n\in (0,1)$
,
![]() $|d_j-d^{G_m}_j-p_m d_j| \le \xi p_m d_j$
for all
$|d_j-d^{G_m}_j-p_m d_j| \le \xi p_m d_j$
for all
![]() $j \in [n]$
with probability at least
$j \in [n]$
with probability at least
![]() $1-\exp \left (-\Omega (\xi ^2 p_m d_j)+2\log n\right )$
.
$1-\exp \left (-\Omega (\xi ^2 p_m d_j)+2\log n\right )$
.
Proof. Take
![]() $G \sim{\mathcal G}(n, \textbf{d})$
and let
$G \sim{\mathcal G}(n, \textbf{d})$
and let
![]() $\textbf{h} = (h_1, \dots, h_n)$
be the degree sequence of the graph
$\textbf{h} = (h_1, \dots, h_n)$
be the degree sequence of the graph
![]() $H$
obtained by independently keeping every edge of
$H$
obtained by independently keeping every edge of
![]() $G$
with probability
$G$
with probability
![]() $p_m$
. Then,
$p_m$
. Then,
![]() $h_j \sim{\textbf{Bin}}(d_j, p_m)$
for every
$h_j \sim{\textbf{Bin}}(d_j, p_m)$
for every
![]() $j\in [n]$
. By Lemma 2.3, conditioned on the event that
$j\in [n]$
. By Lemma 2.3, conditioned on the event that
![]() $|E(H)| = \|\textbf{d}\|_1/2-m$
,
$|E(H)| = \|\textbf{d}\|_1/2-m$
,
![]() $\textbf{h}$
has the same distribution as
$\textbf{h}$
has the same distribution as
![]() $\textbf{d}-\textbf{d}^{G_m}$
. Therefore, by Lemma 2.5 (a,b), for every
$\textbf{d}-\textbf{d}^{G_m}$
. Therefore, by Lemma 2.5 (a,b), for every
![]() $j\in [n]$
,
$j\in [n]$
,
 \begin{eqnarray*}{\mathbb P}(|d_j-d_j^{G_m}-p_m d_j| \ge \xi p_m d_j) &\le & \frac{{\mathbb P}(|h_j-p_md_j| \ge \xi p_m d_j)}{{\mathbb P}(|E(H)| = \|\textbf{d}\|_1/2-m)} \le \frac{2e^{-\frac{\xi ^2}{2+\xi }p_md_j}}{\frac{1}{3}(p_m(1-p_m)\|\textbf{d}\|_1/2)^{-1/2}}\\ & \le & \sqrt{\|\textbf{d}\|_1} \cdot e^{-\Omega (\xi ^2 p_m d_j)} = \exp \left (-\Omega (\xi ^2 p_m d_j)+\log n\right ), \end{eqnarray*}
\begin{eqnarray*}{\mathbb P}(|d_j-d_j^{G_m}-p_m d_j| \ge \xi p_m d_j) &\le & \frac{{\mathbb P}(|h_j-p_md_j| \ge \xi p_m d_j)}{{\mathbb P}(|E(H)| = \|\textbf{d}\|_1/2-m)} \le \frac{2e^{-\frac{\xi ^2}{2+\xi }p_md_j}}{\frac{1}{3}(p_m(1-p_m)\|\textbf{d}\|_1/2)^{-1/2}}\\ & \le & \sqrt{\|\textbf{d}\|_1} \cdot e^{-\Omega (\xi ^2 p_m d_j)} = \exp \left (-\Omega (\xi ^2 p_m d_j)+\log n\right ), \end{eqnarray*}
as
![]() $\|\textbf{d}\|_1\le n^2$
. The lemma follows by taking the union bound over
$\|\textbf{d}\|_1\le n^2$
. The lemma follows by taking the union bound over
![]() $j\in [n]$
.
$j\in [n]$
.
2.4 Couple the two sequential sampling procedures
Finally we couple the two aforementioned procedures and define procedure Coupling(
![]() $\textbf{d}$
,
$\textbf{d}$
,
![]() $\lambda$
,
$\lambda$
,
![]() $\Lambda$
) which sequentially constructs
$\Lambda$
) which sequentially constructs
![]() ${\mathcal G}(n,W)$
and
${\mathcal G}(n,W)$
and
![]() ${\mathcal G}(n,\textbf{d})$
together. The central idea of Coupling is that marginally, the constructions of
${\mathcal G}(n,\textbf{d})$
together. The central idea of Coupling is that marginally, the constructions of
![]() $G_L\sim{\mathcal G}(n,W)$
and
$G_L\sim{\mathcal G}(n,W)$
and
![]() $G\sim{\mathcal G}(n,\textbf{d})$
follow precisely the procedures SeqApprox-P and SeqSample-D, respectively. As in SeqApprox-P, edges
$G\sim{\mathcal G}(n,\textbf{d})$
follow precisely the procedures SeqApprox-P and SeqSample-D, respectively. As in SeqApprox-P, edges
![]() $jk$
in
$jk$
in
![]() $K_n$
are sequentially sampled independently with probability proportional to
$K_n$
are sequentially sampled independently with probability proportional to
![]() $d_jd_k$
. If
$d_jd_k$
. If
![]() $jk$
was already added to
$jk$
was already added to
![]() $G$
then
$G$
then
![]() $jk$
is accepted by
$jk$
is accepted by
![]() $G_L$
with probability
$G_L$
with probability
![]() $\Lambda _{jk}$
as in SeqApprox-P. If
$\Lambda _{jk}$
as in SeqApprox-P. If
![]() $jk$
was not in
$jk$
was not in
![]() $G$
, then
$G$
, then
![]() $jk$
is accepted to
$jk$
is accepted to
![]() $G$
with some probability
$G$
with some probability
![]() $\eta _{jk}$
so that the probability that
$\eta _{jk}$
so that the probability that
![]() $jk$
is selected and accepted by
$jk$
is selected and accepted by
![]() $G$
is proportional to the probability that
$G$
is proportional to the probability that
![]() $jk$
is in
$jk$
is in
![]() ${\mathcal G}(n,\textbf{d})$
, conditional on the current construction of
${\mathcal G}(n,\textbf{d})$
, conditional on the current construction of
![]() $G$
, as desired in SeqSample-D. On the other hand,
$G$
, as desired in SeqSample-D. On the other hand,
![]() $jk$
is accepted by
$jk$
is accepted by
![]() $G_L$
with probability
$G_L$
with probability
![]() $\Lambda _{jk}$
as required by SeqApprox-P. If
$\Lambda _{jk}$
as required by SeqApprox-P. If
![]() $\eta _{jk}\ge \Lambda _{jk}$
then we can couple the two operations so that
$\eta _{jk}\ge \Lambda _{jk}$
then we can couple the two operations so that
![]() $jk$
is added to
$jk$
is added to
![]() $G_L$
only when it is added to
$G_L$
only when it is added to
![]() $G$
. On the other hand, if
$G$
. On the other hand, if
![]() $\eta _{jk}\lt \Lambda _{jk}$
then we simply sample
$\eta _{jk}\lt \Lambda _{jk}$
then we simply sample
![]() $G_L\sim{\mathcal G}(n,W)$
and
$G_L\sim{\mathcal G}(n,W)$
and
![]() $G\sim{\mathcal G}(n,\textbf{d})$
independently. We can prove that the latter case happens rarely. The formal description of Coupling is given below.
$G\sim{\mathcal G}(n,\textbf{d})$
independently. We can prove that the latter case happens rarely. The formal description of Coupling is given below.

Lemma 2.7.
Let
![]() $(G_L,G)$
be the output of Coupling(
$(G_L,G)$
be the output of Coupling(
![]() $\textbf{d},\lambda, \Lambda$
).
$\textbf{d},\lambda, \Lambda$
).
-
(a)
 $G_L\sim{\mathcal G}(n, f(\Lambda \odot Q))$
where
$G_L\sim{\mathcal G}(n, f(\Lambda \odot Q))$
where
 $Q=Q(\textbf{d})$
and
$Q=Q(\textbf{d})$
and
 $f(x)=1-\exp (-\lambda x)$
.
$f(x)=1-\exp (-\lambda x)$
. -
(b)
 $G\sim{\mathcal G}(n,\textbf{d})$
.
$G\sim{\mathcal G}(n,\textbf{d})$
. -
(c) If IndSample(
 $\textbf{d},\lambda, \Lambda$
) is not called during the execution of Coupling(
$\textbf{d},\lambda, \Lambda$
) is not called during the execution of Coupling(
 $\textbf{d},\lambda, \Lambda$
), then
$\textbf{d},\lambda, \Lambda$
), then
 $G_L\subseteq G$
in the output of Coupling(
$G_L\subseteq G$
in the output of Coupling(
 $\textbf{d},\lambda, \Lambda$
).
$\textbf{d},\lambda, \Lambda$
).
Proof. Parts (a,b) are trivially true if IndSample(
![]() $\textbf{d},\zeta$
) is called. Now assume that IndSample(
$\textbf{d},\zeta$
) is called. Now assume that IndSample(
![]() $\textbf{d},\zeta$
) is not called. Part (c) follows directly by the coupling procedure, as every edge is added to
$\textbf{d},\zeta$
) is not called. Part (c) follows directly by the coupling procedure, as every edge is added to
![]() $G_L$
only when it is, or has been added to
$G_L$
only when it is, or has been added to
![]() $G$
. For (a), note that if IndSample(
$G$
. For (a), note that if IndSample(
![]() $\textbf{d},\zeta$
) is not called then the edges are sequentially added to
$\textbf{d},\zeta$
) is not called then the edges are sequentially added to
![]() $G_L$
exactly as in SeqApprox-P(
$G_L$
exactly as in SeqApprox-P(
![]() $\textbf{d}, \lambda, \Lambda$
), and thus part (a) follows by Lemma 2.2. For part (b), notice that in each step
$\textbf{d}, \lambda, \Lambda$
), and thus part (a) follows by Lemma 2.2. For part (b), notice that in each step
![]() $i$
, edge
$i$
, edge
![]() $jk$
is added to
$jk$
is added to
![]() $G_{i-1}$
with probability
$G_{i-1}$
with probability
![]() $Q_{jk}\eta _{jk}^{(i)}$
, which is proportional
$Q_{jk}\eta _{jk}^{(i)}$
, which is proportional
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}) \mid G_{i-1})$
. Thus, the edges are added to
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}) \mid G_{i-1})$
. Thus, the edges are added to
![]() $G$
exactly as in the execution of SeqSample-D(
$G$
exactly as in the execution of SeqSample-D(
![]() $\textbf{d}$
), and part (b) follows by Corollary 2.4.
$\textbf{d}$
), and part (b) follows by Corollary 2.4.
2.5 Specify
 $\lambda$
and
$\lambda$
and
 $\Lambda$
for the coupling procedure
$\Lambda$
for the coupling procedure
By the assumptions
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
and
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
and
![]() $\delta (\textbf{d})\gg \log n$
, there exist
$\delta (\textbf{d})\gg \log n$
, there exist
![]() $\xi, \zeta, \zeta '=o(1)$
that go to zero sufficiently slowly so that
$\xi, \zeta, \zeta '=o(1)$
that go to zero sufficiently slowly so that
To see why they exist, notice that there exists
![]() $\zeta '=o(1)$
satisfying [4] since
$\zeta '=o(1)$
satisfying [4] since
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
. Moreover, since
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
. Moreover, since
![]() $\delta (\textbf{d})\gg \log n$
, we may assume that
$\delta (\textbf{d})\gg \log n$
, we may assume that
![]() $\zeta '$
goes to 0 sufficiently slowly so that [2] is satisfied and there exists
$\zeta '$
goes to 0 sufficiently slowly so that [2] is satisfied and there exists
![]() $\xi$
satisfying [3]. Finally, given [4] and
$\xi$
satisfying [3]. Finally, given [4] and
![]() $\xi =o(1)$
, the right-hand side of [5] is
$\xi =o(1)$
, the right-hand side of [5] is
![]() $o(1)$
, and hence there exists
$o(1)$
, and hence there exists
![]() $\zeta$
satisfying [5].
$\zeta$
satisfying [5].
Choose
![]() $\xi, \zeta, \zeta '$
that satisfy all the conditions above. For the coupling procedure, we set
$\xi, \zeta, \zeta '$
that satisfy all the conditions above. For the coupling procedure, we set
3. Proof of Theorem1.8
Let
![]() $\Delta =\Delta (\textbf{d})$
,
$\Delta =\Delta (\textbf{d})$
,
![]() $Q=Q(\textbf{d})$
, and
$Q=Q(\textbf{d})$
, and
![]() $P=P(\textbf{d})$
. By Lemma 2.7, it suffices to show that
$P=P(\textbf{d})$
. By Lemma 2.7, it suffices to show that
as
![]() $1-\exp (-(1+o(1))P_{ij})=(1+o(1))(1-e^{-P_{ij}})$
for every
$1-\exp (-(1+o(1))P_{ij})=(1+o(1))(1-e^{-P_{ij}})$
for every
![]() $ij$
.
$ij$
.
Proof of
(9). For every
![]() $1\le j\lt k\le n$
,
$1\le j\lt k\le n$
,
Since
![]() $\lambda = (1-\zeta ')\|\textbf{d}\|_1/2$
by [6], and by [7]
$\lambda = (1-\zeta ')\|\textbf{d}\|_1/2$
by [6], and by [7]
 \begin{align*} \lambda \Lambda _{jk} Q_{jk} & = \frac {(1-\zeta ') \|\textbf {d}\|_1}{2} \frac {(1-\zeta )\|\textbf {d}\|_1}{\|\textbf {d}\|_1+d_jd_k} \frac {2d_jd_k}{\|\textbf {d}\|_1^2(1+ O(\Delta /\|\textbf {d}\|_1) } \\ & = \left (1+O\left (\zeta +\zeta '+\frac {\Delta }{\|\textbf {d}\|_1}\right )\right ) \frac {d_jd_k}{\|\textbf {d}\|_1+d_jd_k}, \end{align*}
\begin{align*} \lambda \Lambda _{jk} Q_{jk} & = \frac {(1-\zeta ') \|\textbf {d}\|_1}{2} \frac {(1-\zeta )\|\textbf {d}\|_1}{\|\textbf {d}\|_1+d_jd_k} \frac {2d_jd_k}{\|\textbf {d}\|_1^2(1+ O(\Delta /\|\textbf {d}\|_1) } \\ & = \left (1+O\left (\zeta +\zeta '+\frac {\Delta }{\|\textbf {d}\|_1}\right )\right ) \frac {d_jd_k}{\|\textbf {d}\|_1+d_jd_k}, \end{align*}
and (9) follows by noting that
![]() $\zeta, \zeta ',\Delta /\|\textbf{d}\|_1=o(1)$
.
$\zeta, \zeta ',\Delta /\|\textbf{d}\|_1=o(1)$
.
Proof of
(8). By Lemma 2.5(c) (with
![]() $\mu =\lambda$
and
$\mu =\lambda$
and
![]() ${\epsilon }=\lambda ^{-1/3}$
) and [6], a.a.s.
${\epsilon }=\lambda ^{-1/3}$
) and [6], a.a.s.
![]() ${\mathcal I}=(1+O(\lambda ^{-1/3}))\lambda = (1-\zeta '+O(\|\textbf{d}\|_1^{-1/3}))\|\textbf{d}\|_1/2$
. It suffices then to show that a.a.s. throughout the execution of Coupling(
${\mathcal I}=(1+O(\lambda ^{-1/3}))\lambda = (1-\zeta '+O(\|\textbf{d}\|_1^{-1/3}))\|\textbf{d}\|_1/2$
. It suffices then to show that a.a.s. throughout the execution of Coupling(
![]() $\textbf{d},\lambda, \Lambda$
),
$\textbf{d},\lambda, \Lambda$
),
![]() $\eta ^{(i)}_{x_i}\ge \Lambda _{x_i}$
for every
$\eta ^{(i)}_{x_i}\ge \Lambda _{x_i}$
for every
![]() $1\le i\le{\mathcal I}$
, where
$1\le i\le{\mathcal I}$
, where
![]() $x_i$
is the random edge sampled in the
$x_i$
is the random edge sampled in the
![]() $i$
th iteration. Let
$i$
th iteration. Let
![]() $m_i$
be the number of edges in
$m_i$
be the number of edges in
![]() $G_i$
. Since a.a.s.
$G_i$
. Since a.a.s.
![]() ${\mathcal I}=(1-\zeta '+O(\|\textbf{d}\|_1^{-1/3}))\|\textbf{d}\|_1/2$
and
${\mathcal I}=(1-\zeta '+O(\|\textbf{d}\|_1^{-1/3}))\|\textbf{d}\|_1/2$
and
![]() $m_i\le{\mathcal I}$
for every
$m_i\le{\mathcal I}$
for every
![]() $1\le i\le{\mathcal I}$
, it follows then by [2] that a.a.s.
$1\le i\le{\mathcal I}$
, it follows then by [2] that a.a.s.
where
![]() $p_{m_i}$
is defined by
$p_{m_i}$
is defined by
![]() $1-2m_i/\|\textbf{d}\|_1$
as in Lemma 2.6.
$1-2m_i/\|\textbf{d}\|_1$
as in Lemma 2.6.
By Lemma 2.6 (with
![]() $\xi$
chosen in Section 2.5), [10] and [3], with probability at least
$\xi$
chosen in Section 2.5), [10] and [3], with probability at least
we have that
![]() $|d_j-d^{G_i}_j-p_{m_i} d_j| \le \xi p_{m_i} d_j$
for all
$|d_j-d^{G_i}_j-p_{m_i} d_j| \le \xi p_{m_i} d_j$
for all
![]() $j \in [n]$
. Now take the union bound over all the
$j \in [n]$
. Now take the union bound over all the
![]() ${\mathcal I}\le \|\textbf{d}\|_1/2$
steps, we conclude that
${\mathcal I}\le \|\textbf{d}\|_1/2$
steps, we conclude that
Next, we estimate
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}) \mid G_i)$
. Note that Proposition 1.3 gives
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}) \mid G_i)$
. Note that Proposition 1.3 gives
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}) \mid G_i)$
when
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}) \mid G_i)$
when
![]() $G_i=\emptyset$
. Here, we apply another corollary of [Reference Gao and Ohapkin20], [Theorem 1], given in Theorem3.1 below, which estimates the edge probabilities in
$G_i=\emptyset$
. Here, we apply another corollary of [Reference Gao and Ohapkin20], [Theorem 1], given in Theorem3.1 below, which estimates the edge probabilities in
![]() ${\mathcal G}(n,\textbf{d})$
when conditioned on a set of edges
${\mathcal G}(n,\textbf{d})$
when conditioned on a set of edges
![]() $H$
being present in
$H$
being present in
![]() ${\mathcal G}(n,\textbf{d})$
.
${\mathcal G}(n,\textbf{d})$
.
For two degree sequences
![]() $\textbf{d}$
and
$\textbf{d}$
and
![]() $\textbf{g}$
, we say
$\textbf{g}$
, we say
![]() $\textbf{d}\preceq \textbf{g}$
if
$\textbf{d}\preceq \textbf{g}$
if
![]() $d_i\le g_i$
for every
$d_i\le g_i$
for every
![]() $i\in [n]$
. Given a graph
$i\in [n]$
. Given a graph
![]() $H$
on
$H$
on
![]() $[n]$
, let
$[n]$
, let
![]() $\textbf{d}^H$
denote the degree sequence of
$\textbf{d}^H$
denote the degree sequence of
![]() $H$
.
$H$
.
Theorem 3.1.
Suppose
![]() $H$
is a graph on
$H$
is a graph on
![]() $[n]$
with
$[n]$
with
![]() $\textbf{d}^{H}\preceq \textbf{d}$
, and let
$\textbf{d}^{H}\preceq \textbf{d}$
, and let
![]() $\textbf{t} = \textbf{d}-\textbf{d}^H$
. Suppose that
$\textbf{t} = \textbf{d}-\textbf{d}^H$
. Suppose that
![]() $J(\textbf{d})=o(\|\textbf{t}\|_1)$
and suppose
$J(\textbf{d})=o(\|\textbf{t}\|_1)$
and suppose
![]() $jk \not \in H$
. Then
$jk \not \in H$
. Then
where
![]() ${\mathbb P}(jk \in{\mathcal G}(n, \textbf{d}) \mid H)$
denotes the probability that
${\mathbb P}(jk \in{\mathcal G}(n, \textbf{d}) \mid H)$
denotes the probability that
![]() $jk\in{\mathcal G}(n,\textbf{d})$
conditional on the event that
$jk\in{\mathcal G}(n,\textbf{d})$
conditional on the event that
![]() ${\mathcal G}(n,\textbf{d})$
contains
${\mathcal G}(n,\textbf{d})$
contains
![]() $H$
as a subgraph.
$H$
as a subgraph.
We first verify that the assumption
![]() $J(\textbf{d})=o(\|\textbf{t}\|_1)$
of Theorem3.1 is satisfied for every
$J(\textbf{d})=o(\|\textbf{t}\|_1)$
of Theorem3.1 is satisfied for every
![]() $i\le{\mathcal I}$
with
$i\le{\mathcal I}$
with
![]() $H=G_i$
. By (10) we may assume that
$H=G_i$
. By (10) we may assume that
![]() $p_{m_i}\ge \zeta '/2$
for every
$p_{m_i}\ge \zeta '/2$
for every
![]() $1\le i\le{\mathcal I}$
(which holds a.a.s.). Let
$1\le i\le{\mathcal I}$
(which holds a.a.s.). Let
![]() $\textbf{t}_i=\textbf{d}-\textbf{d}^{G_i}$
. Then,
$\textbf{t}_i=\textbf{d}-\textbf{d}^{G_i}$
. Then,
By [4],
![]() $J(\textbf{d})\ll \zeta ' \|\textbf{d}\|_1$
and consequently
$J(\textbf{d})\ll \zeta ' \|\textbf{d}\|_1$
and consequently
![]() $J(\textbf{d})/\|\textbf{t}_i\|_1=O(J(\textbf{d})/\zeta '\|\textbf{d}\|_1)=o(1)$
for every
$J(\textbf{d})/\|\textbf{t}_i\|_1=O(J(\textbf{d})/\zeta '\|\textbf{d}\|_1)=o(1)$
for every
![]() $1\le i\le{\mathcal I}$
. By Theorem3.1, [11] and [12], a.a.s.
$1\le i\le{\mathcal I}$
. By Theorem3.1, [11] and [12], a.a.s.
where
![]() $J(\textbf{d})/p_{m_i}\|\textbf{d}\|_1 + \xi = O(J(\textbf{d})/\zeta '\|\textbf{d}\|_1 + \xi )=o(1)$
as shown before. Recall that
$J(\textbf{d})/p_{m_i}\|\textbf{d}\|_1 + \xi = O(J(\textbf{d})/\zeta '\|\textbf{d}\|_1 + \xi )=o(1)$
as shown before. Recall that
It follows that
Notice that
Thus,
Hence,
Acknowledgement
We thank two anonymous referees for their valuable advice in improving the presentation of the paper.
Funding statement
Research supported by NSERC RGPIN-04173-2019.
Appendix
We prove a few properties of degree sequences
![]() $\textbf{d}$
where
$\textbf{d}$
where
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
Proposition 3.2.
Let
![]() $\textbf{d}=\textbf{d}_n$
be a sequence of degree sequences such that
$\textbf{d}=\textbf{d}_n$
be a sequence of degree sequences such that
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
. Let
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
. Let
![]() $\Delta =\max \{d_i,i\in [n]\}$
. Then,
$\Delta =\max \{d_i,i\in [n]\}$
. Then,
-
(a)
 $\Delta =o(n)$
.
$\Delta =o(n)$
. -
(b) For every
 ${\epsilon }\gt 0$
,
${\epsilon }\gt 0$
,
 $ |\{ij: d_id_j\ge{\epsilon } \|\textbf{d}\|_1\}|\le{\epsilon } n^2$
for all sufficiently large
$ |\{ij: d_id_j\ge{\epsilon } \|\textbf{d}\|_1\}|\le{\epsilon } n^2$
for all sufficiently large
 $n$
.
$n$
.
Proof.
For (a), suppose on the contrary that
![]() $\Delta \ge \delta n$
for some absolute constant
$\Delta \ge \delta n$
for some absolute constant
![]() $\delta \gt 0$
. Then,
$\delta \gt 0$
. Then,
 \begin{equation*} \|\textbf {d}\|_1=\sum _{i=1}^n d_i \le \delta ^{-1} \sum _{i=1}^{\delta n} d_i \le \delta ^{-1} J(\textbf {d}), \end{equation*}
\begin{equation*} \|\textbf {d}\|_1=\sum _{i=1}^n d_i \le \delta ^{-1} \sum _{i=1}^{\delta n} d_i \le \delta ^{-1} J(\textbf {d}), \end{equation*}
contradicting with
![]() $J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
$J(\textbf{d})=o(\|\textbf{d}\|_1)$
.
For (b), note that
![]() $J(\textbf{d})\ge \Delta d_{\Delta }$
and thus
$J(\textbf{d})\ge \Delta d_{\Delta }$
and thus
![]() $\Delta d_{\Delta } = o(\|\textbf{d}\|_1)$
. It follows that for every
$\Delta d_{\Delta } = o(\|\textbf{d}\|_1)$
. It follows that for every
![]() $i,j \in [n]$
such that
$i,j \in [n]$
such that
![]() $j\ge \Delta$
,
$j\ge \Delta$
,
![]() $d_id_j \le \Delta d_{\Delta } = o(\|\textbf{d}\|_1)$
. Thus, part (b) follows by
$d_id_j \le \Delta d_{\Delta } = o(\|\textbf{d}\|_1)$
. Thus, part (b) follows by
![]() $\Delta =o(n)$
from part (a).
$\Delta =o(n)$
from part (a).
Example 3.3.
We construct an example of degree sequences
![]() $\textbf{d}\preceq \textbf{g}$
for which there exists
$\textbf{d}\preceq \textbf{g}$
for which there exists
![]() $jk$
such that
$jk$
such that
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))= 1-o(1)$
and
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{d}))= 1-o(1)$
and
![]() ${\mathbb P}(jk\in{\mathcal G}(n,\textbf{g}))=o(1)$
. Let
${\mathbb P}(jk\in{\mathcal G}(n,\textbf{g}))=o(1)$
. Let
![]() $\textbf{t}$
be a degree sequence where
$\textbf{t}$
be a degree sequence where
![]() $t_1=t_2=n^{2/3}$
, and
$t_1=t_2=n^{2/3}$
, and
![]() $t_3=\cdots =t_n=1$
(without loss of generality we assume that
$t_3=\cdots =t_n=1$
(without loss of generality we assume that
![]() $n^{2/3}$
is an integer and
$n^{2/3}$
is an integer and
![]() $\|\textbf{t}\|_1$
is even). Let
$\|\textbf{t}\|_1$
is even). Let
![]() $\textbf{g}=(n-1)\textbf{1}-\textbf{t}$
, and let
$\textbf{g}=(n-1)\textbf{1}-\textbf{t}$
, and let
![]() $\textbf{d}$
be
$\textbf{d}$
be
![]() $(n-2n^{2/3})$
-regular. Obviously,
$(n-2n^{2/3})$
-regular. Obviously,
![]() $\textbf{d}\preceq \textbf{g}$
. By symmetry, the probability that vertices 1 and 2 are adjacent in
$\textbf{d}\preceq \textbf{g}$
. By symmetry, the probability that vertices 1 and 2 are adjacent in
![]() ${\mathcal G}(n,\textbf{d})$
is equal to
${\mathcal G}(n,\textbf{d})$
is equal to
![]() $(n-2n^{2/3})/(n-1)=1-o(1)$
. By Proposition 1.3
, the probability that these two vertices are adjacent in
$(n-2n^{2/3})/(n-1)=1-o(1)$
. By Proposition 1.3
, the probability that these two vertices are adjacent in
![]() ${\mathcal G}(n,\textbf{t})$
is
${\mathcal G}(n,\textbf{t})$
is
![]() $1-o(1)$
, and consequently, their adjacency probability in
$1-o(1)$
, and consequently, their adjacency probability in
![]() ${\mathcal G}(n,\textbf{g})$
is
${\mathcal G}(n,\textbf{g})$
is
![]() $o(1)$
, as
$o(1)$
, as
![]() ${\mathcal G}(n,\textbf{g})$
has the same distribution as the complement of
${\mathcal G}(n,\textbf{g})$
has the same distribution as the complement of
![]() ${\mathcal G}(n,\textbf{t})$
.
${\mathcal G}(n,\textbf{t})$
.