Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Austin, Tim
2008.
On exchangeable random variables and the statistics of large graphs and hypergraphs.
Probability Surveys,
Vol. 5,
Issue. none,
Lo, Allan
2009.
Cliques in graphs with bounded minimum degree.
Electronic Notes in Discrete Mathematics,
Vol. 34,
Issue. ,
p.
163.
Shapira, Asaf
and
Yuster, Raphael
2010.
On the density of a graph and its blowup.
Journal of Combinatorial Theory, Series B,
Vol. 100,
Issue. 6,
p.
704.
Hatami, Hamed
2010.
Graph norms and Sidorenko’s conjecture.
Israel Journal of Mathematics,
Vol. 175,
Issue. 1,
p.
125.
Conlon, David
Fox, Jacob
and
Sudakov, Benny
2010.
An Approximate Version of Sidorenko’s Conjecture.
Geometric and Functional Analysis,
Vol. 20,
Issue. 6,
p.
1354.
Razborov, Alexander A.
2010.
On 3-Hypergraphs with Forbidden 4-Vertex Configurations.
SIAM Journal on Discrete Mathematics,
Vol. 24,
Issue. 3,
p.
946.
Gromov, Mikhail
2010.
Singularities, Expanders and Topology of Maps. Part 2: from Combinatorics to Topology Via Algebraic Isoperimetry.
Geometric and Functional Analysis,
Vol. 20,
Issue. 2,
p.
416.
Pikhurko, Oleg
2010.
An analytic approach to stability.
Discrete Mathematics,
Vol. 310,
Issue. 21,
p.
2951.
Nikiforov, V.
2010.
The number of cliques in graphs of given order and size.
Transactions of the American Mathematical Society,
Vol. 363,
Issue. 3,
p.
1599.
Allen, Peter
Böttcher, Julia
Hladký, Jan
and
Piguet, Diana
2011.
A density Corrádi-Hajnal theorem.
Electronic Notes in Discrete Mathematics,
Vol. 38,
Issue. ,
p.
31.
Razborov, Alexander A.
2011.
On the Fon-Der-Flaass interpretation of extremal examples for Turán’s (3, 4)-problem.
Proceedings of the Steklov Institute of Mathematics,
Vol. 274,
Issue. 1,
p.
247.
Lovász, L.
and
Szegedy, B.
2011.
Finitely forcible graphons.
Journal of Combinatorial Theory, Series B,
Vol. 101,
Issue. 5,
p.
269.
LO, ALLAN
2012.
Cliques in Graphs With Bounded Minimum Degree.
Combinatorics, Probability and Computing,
Vol. 21,
Issue. 3,
p.
457.
Das, Shagnik
Huang, Hao
Ma, Jie
Naves, Humberto
and
Sudakov, Benny
2013.
A problem of Erdős on the minimum number of k -cliques.
Journal of Combinatorial Theory, Series B,
Vol. 103,
Issue. 3,
p.
344.
CSIKVÁRI, PÉTER
2013.
Note on the Smallest Root of the Independence Polynomial.
Combinatorics, Probability and Computing,
Vol. 22,
Issue. 1,
p.
1.
Ugander, Johan
Backstrom, Lars
and
Kleinberg, Jon
2013.
Subgraph frequencies.
p.
1307.
Mohar, Bojan
2013.
Handbook of Graph Theory, Second Edition.
Vol. 20134658,
Issue. ,
p.
1038.
Ilić, Aleksandar
and
Milosavljević, Nikola
2013.
The weighted vertex PI index.
Mathematical and Computer Modelling,
Vol. 57,
Issue. 3-4,
p.
623.
Mubayi, Dhruv
2013.
Counting substructures II: Hypergraphs.
Combinatorica,
Vol. 33,
Issue. 5,
p.
591.
Harangi, Viktor
2013.
On the density of triangles and squares in regular finite and unimodular random graphs.
Combinatorica,
Vol. 33,
Issue. 5,
p.
531.


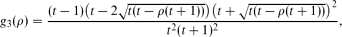
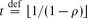 is the integer such that
is the integer such that 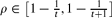 .
.