Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Katz, Nets Hawk
and
Koester, Paul
2010.
On Additive Doubling and Energy.
SIAM Journal on Discrete Mathematics,
Vol. 24,
Issue. 4,
p.
1684.
Tokushige, Norihide
2011.
A product version of the Erdős–Ko–Rado theorem.
Journal of Combinatorial Theory, Series A,
Vol. 118,
Issue. 5,
p.
1575.
Ben-Sasson, Eli
Lovett, Shachar
and
Ron-Zewi, Noga
2012.
An Additive Combinatorics Approach Relating Rank to Communication Complexity.
p.
177.
EVEN-ZOHAR, CHAIM
2012.
On Sums of Generating Sets in ℤ2n.
Combinatorics, Probability and Computing,
Vol. 21,
Issue. 6,
p.
916.
Lovett, Shachar
2012.
Equivalence of polynomial conjectures in additive combinatorics.
Combinatorica,
Vol. 32,
Issue. 5,
p.
607.
Sanders, Tom
2012.
The structure theory of set addition revisited.
Bulletin of the American Mathematical Society,
Vol. 50,
Issue. 1,
p.
93.
Breuillard, Emmanuel
Green, Ben
and
Tao, Terence
2013.
Erdős Centennial.
Vol. 25,
Issue. ,
p.
129.
Bibak, Khodakhast
2013.
Number Theory and Related Fields.
Vol. 43,
Issue. ,
p.
99.
Even-Zohar, Chaim
and
Lev, Vsevolod F.
2013.
Small asymmetric sumsets in elementary abelian 2-groups.
Discrete Mathematics,
Vol. 313,
Issue. 5,
p.
689.
Even-Zohar, Chaim
and
Lovett, Shachar
2014.
The Freiman–Ruzsa theorem over finite fields.
Journal of Combinatorial Theory, Series A,
Vol. 125,
Issue. ,
p.
333.
Schoen, Tomasz
and
Shkredov, Ilya D.
2014.
Roth’s theorem in many variables.
Israel Journal of Mathematics,
Vol. 199,
Issue. 1,
p.
287.
FREIMAN, GREGORY
HERZOG, MARCEL
LONGOBARDI, PATRIZIA
and
MAJ, MERCEDE
2014.
SMALL DOUBLING IN ORDERED GROUPS.
Journal of the Australian Mathematical Society,
Vol. 96,
Issue. 3,
p.
316.
Dell, Holger
and
Van Melkebeek, Dieter
2014.
Satisfiability Allows No Nontrivial Sparsification unless the Polynomial-Time Hierarchy Collapses.
Journal of the ACM,
Vol. 61,
Issue. 4,
p.
1.
Ben-Sasson, Eli
Lovett, Shachar
and
Ron-Zewi, Noga
2014.
An Additive Combinatorics Approach Relating Rank to Communication Complexity.
Journal of the ACM,
Vol. 61,
Issue. 4,
p.
1.
Nathanson, M. B.
2014.
Growth Polynomials for Additive Quadruples and (h, k)-Tuples.
Acta Mathematica Hungarica,
Vol. 143,
Issue. 1,
p.
44.
Shkredov, Ilya Dmitrievich
2015.
Структурные теоремы в аддитивной комбинаторике.
Успехи математических наук,
Vol. 70,
Issue. 1(421),
p.
123.
Wolf, J.
2015.
Finite field models in arithmetic combinatorics – ten years on.
Finite Fields and Their Applications,
Vol. 32,
Issue. ,
p.
233.
Sanders, Tom
2015.
A statistical approach to covering lemmas.
European Journal of Combinatorics,
Vol. 48,
Issue. ,
p.
19.
Kirshner, Naomi
and
Samorodnitsky, Alex
2020.
On the ℓ4:ℓ2 ratio of functions with restricted Fourier support.
Journal of Combinatorial Theory, Series A,
Vol. 172,
Issue. ,
p.
105202.
Xie, Ning
Xu, Shuai
and
Xu, Yekun
2021.
Computer Science – Theory and Applications.
Vol. 12730,
Issue. ,
p.
460.
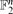 : if
: if  is a set for which |A + A| ≤ K|A| then A is contained in a subspace of size
is a set for which |A + A| ≤ K|A| then A is contained in a subspace of size 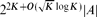 ; except for the
; except for the 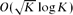 error, this is best possible. If in addition we assume that A is a downset, then we can also cover A by O(K46) translates of a coordinate subspace of size at most |A|, thereby verifying the so-called polynomial Freiman–Ruzsa conjecture in this case. A common theme in the arguments is the use of compression techniques. These have long been familiar in extremal set theory, but have been used only rarely in the additive combinatorics literature.
error, this is best possible. If in addition we assume that A is a downset, then we can also cover A by O(K46) translates of a coordinate subspace of size at most |A|, thereby verifying the so-called polynomial Freiman–Ruzsa conjecture in this case. A common theme in the arguments is the use of compression techniques. These have long been familiar in extremal set theory, but have been used only rarely in the additive combinatorics literature.