Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T04:38:25.025Z Has data issue: false hasContentIssue false
  • English
  • Français

The Zeroes of Functions Related to Dirichlet L-Functions

Published online by Cambridge University Press:  20 November 2018

Lenrd Weinstein
Lenrd Weinstein*
Affiliation:
Department of Mathematics, Temple University, Philadelphia, Pennsylvania 19122
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Hecke, [3], has shown for x a real Dirichlet character modulo q, the associated Dirichlet L-function L(s, x) has infinitely many zeroes on the line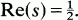

Here, using a method of Polya, [5], we show that both the real and imaginary parts of a function associated to L(s, x) through the functional equation, have infinitely many zeroes on any line

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 24 , Issue 1 , 01 March 1981 , pp. 53 - 57
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Berlowitz, B., Extensions of a theorem of Hardy, Acta Arithmetic. 14 (1962), 203-207.Google Scholar
2. Davenport, H., Multiplicative number theory, Markham Publishing Company, Chicago, 1967.Google Scholar
3. Hecke, E., Über Dirichlet-reihen mit funktionalgleichung und ihre nullstellen auf der mittelgeraden, Sitzungsberichte der Bayerischen Akademie der Wissenschaften. Mathematisch—Natur wissenschaftliche Abteilung (1962), 73-95.Google Scholar
4. Lang, S., Algebraic number theory, Addison Wesley Publishing Company, Inc. Reading, Mass., 1970.Google Scholar
5. Pôlya, G., Über die algebraisch-funktion theoretischen Untersuchungen von J. L. W. V. Jensen, Kgl. Danske Videnskabernes Selskab. 7 (1962), No. 17.Google Scholar
6. Titchmarsh, E. C., The theory of the Riemann zeta-function, Clarendon Press, Oxford, 1951.Google Scholar