Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mathieu, Martin
1988.
Elementary operators on prime C*-algebras II.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 3,
p.
275.
Magajna, Bojan
1991.
On the relative reflexivity of finitely generated modules of operators.
Transactions of the American Mathematical Society,
Vol. 327,
Issue. 1,
p.
221.
Magajna, Bojan
1993.
A transitivity theorem for algebras of elementary operators.
Proceedings of the American Mathematical Society,
Vol. 118,
Issue. 1,
p.
119.
Saksman, Eero
and
Tylli, Hans-Olav
1999.
The Apostol–Fialkow Formula for Elementary Operators on Banach Spaces.
Journal of Functional Analysis,
Vol. 161,
Issue. 1,
p.
1.
Mathieu, Martin
2001.
Recent Progress in Functional Analysis, Proceedings of the International Functional Analysis Meeting on the Occasion of the 70th Birthday of Professor Manuel Valdivia.
Vol. 189,
Issue. ,
p.
363.


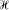 be a separable Hilbert space,
be a separable Hilbert space, 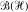 the algebra of all bounded operators on
the algebra of all bounded operators on 