Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T05:58:16.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability on the basis of Orthogonal Trajectories

Published online by Cambridge University Press:  20 November 2018

T. A. Burton
T. A. Burton*
Affiliation:
University of Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a system of differential equations of second order given by

1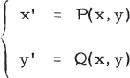

(' = d/dt) where P and Q have continuous first partial derivatives with respect to x and y in some open and simply connected set R containing O = (0, 0) which we assume to be the only singular point in R. In fact, let R be the whole plane; for if not then the following discussion can be modified.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 8 , Issue 5 , October 1965 , pp. 647 - 658
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Lefschetz, S., Differential Equations: Geometric Theory. Interscience Publishers, New York, 1957.Google Scholar
2. Nemystskii, V. and Stepanov, V., Qualitative Theory of Differential Equations, Princeton University Press, Princeton, New Jersey, 1960.Google Scholar
3. Hurewicz, W., Lectures on Ordinary Differential Equations. Wiley and Technology Press of M. I. T., New York, 1958.Google Scholar
4. Pozarickii, G., On non-steady motion of conservative holonomic systems. PMM 20 (1956), pp. 429-433.Google Scholar
5. Hahn, W., Theory and Application of Liapunov' s Direct Method. Prentice-Hall, New Jersey, 1963.Google Scholar
6. Massera, J., Contributions to Stability Theory. Annals of Math., V.64(1956), pp. 184-186.Google Scholar
7. Duff, G., Limit-Cycles and Rotated Vector Fields. Annals of Math., V.57 (1951), pp. 15-31.Google Scholar