Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T16:06:44.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Separating Splitting Tilting Modules and Hereditary Algebras

Published online by Cambridge University Press:  20 November 2018

Ibrahim Assem
Ibrahim Assem*
Affiliation:
Fakultät Für Mathematik Universität Bielefeld 4800, Bielefeld 1 Federal Republic of Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a finite-dimensional algebra over an algebraically closed field. By module is meant a finitely generated right module. A module T^ is called a tilting module if 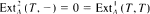and there exists an exact sequence 0 → A^ → T' → T" → 0 with T'. T" direct sums of summands of T. Let B = End T^·T^ is called separating (respectively, splitting) if every indecomposable A-module M (respectively, B-module N) is such that either Hom^(T,M) = 0 or 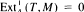(respectively, N ⊗ T = 0 or 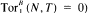. We prove that A is hereditary provided the quiver of A has no oriented cycles and every separating tilting module is splitting.

Keywords

Primary 16A46secondary 16A64Representations of hereditary algebrastilting modules
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 30 , Issue 2 , 01 June 1987 , pp. 177 - 181
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Assem, I. and Happel, D., Generalized tilted algebras of type An , Comm. Algebra 9(20) (1981), pp. 2101–2125.Google Scholar
2. Assem, I., Torsion theories induced by tilting modules, Can. J. Math. 36(5) (1984), pp. 899–913.Google Scholar
3. Auslander, M. and Reiten, I., Modules determined by composition factors, Illinois J. Math. 29(2) (1985), pp. 280–301.Google Scholar
4. Auslander, M., Platzeck, M.I. and Reiten, I., Coxeterfunctors without diagrams, Trans. Amer. Math. Soc. 250(1979), pp. 1–46.Google Scholar
5. Bongartz, K., Tilted algebras, Proc. ICRA III (Puebla, 1980), Springer Lecture Notes No. 903 (1981), pp. 26-38.Google Scholar
6. Gabriel, P., Auslander-Reiten sequences and representation-finite algebras, Proc. ICRA II (Ottawa, 1979), Springer Lecture Notes No. 831 (1980), pp. 1–71.Google Scholar
7. Happel, D. and Ringel, C.M., Tilted algebras, Trans. Amer. Math. Soc. 274(2) (1982), pp. 399–443.Google Scholar
8. Hoshino, M., On splitting torsion theories induced by tilting modules, Comm. Algebra 11(4) (1983), pp. 427–440.Google Scholar
9. Tachikawa, H. and Wakamatsu, T., Applications of reflection functors for selfinjective algebras, Proc. ICRA IV (Ottawa, 1984), Springer Verlag Lecture Notes 1177 (1986), pp. 308–327.Google Scholar