Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T04:47:06.025Z Has data issue: false hasContentIssue false
  • English
  • Français

Ordinary Singularities of Algebraic Curves

Published online by Cambridge University Press:  20 November 2018

Ferruccio Orecchia
Ferruccio Orecchia*
Affiliation:
Istttuto di Matematica Dell, ‘Universita’ di Genova, Via L. B. Alberti, 4, 16132-Genova-Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

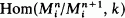Let A be the local ring at a singular point p of an algebraic reduced curve. Let M (resp. Ml,..., Mh) be the maximal ideal of A (resp. of Ā). In this paper we want to classify ordinary singularities p with reduced tangent cone: Spec(G(A)). We prove that G(A) is reduced if and only if: p is an ordinary singularity, and the vector spaces span the vector space 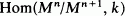. If the points of the projectivized tangent cone Proj(G(A)) are in generic position then p is an ordinary singularity if and only if G(A) is reduced. We give an example which shows that the preceding equivalence is not true in general.

Keywords

13H1514H2014H45Algebraic curveordinary singularitybranchestangent conetangent spaceVeronese embedding
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 24 , Issue 4 , 01 December 1981 , pp. 423 - 431
Copyright
Copyright © Canadian Mathematical Society 1981

References

[D] Davis, E. D., On the geometric interpretation of seminormality, Proc. of A.M.S., Vol. 68, (1978), 1-5.Google Scholar
[F] Fulton, W., Algebraic curves, Mathematics Lecture Note Series, W. A. Benjamin, New York (1969).Google Scholar
[H] Hartshorne, R., Algebraic geometry, Graduate texts in mathematics, Springer Verlag, New York, (1977).Google Scholar
[L] Lipman, J., Stable ideals and Arf rings, Amer. J. Math., Vol. 93, (1971), 649-685.Google Scholar
[M] Mumford, D., Introduction to algebraic geometry, Harvard Lecture Notes, (1967).Google Scholar
[O] Orecchia, F., Points in generic position and conductor of curves with ordinary singularities, Queen's Mathematical Preprint, No. 1979-26.Google Scholar
[S] Sally, J., Number of generators of ideals in local rings, Lect. Notes in Pure and Applied Math., Marcel Dekker, New York, (1978).Google Scholar
[Sh] Shafarevich, I. R., Basic algebraic geometry, Grundlehren 213, Springer Verlag, Heildelberg (1974).Google Scholar