Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
QIAO, PU
and
ZHAN, XINGZHI
2022.
ON A PROBLEM OF ERDŐS ABOUT GRAPHS WHOSE SIZE IS THE TURÁN NUMBER PLUS ONE.
Bulletin of the Australian Mathematical Society,
Vol. 105,
Issue. 2,
p.
177.
Basavaraju, Manu
van Leeuwen, Erik Jan
and
Saei, Reza
2024.
Maximal induced matchings in K4-free and K5-free graphs.
Discrete Applied Mathematics,
Vol. 359,
Issue. ,
p.
407.


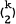 edges. Erdos [1] proved that if a graph G
edges. Erdos [1] proved that if a graph G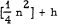 edges, then it contains at least
edges, then it contains at least 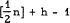 complete 3-graphs if it contains any at all. The main object of this note is to extend this result to complete k-graphs.
complete 3-graphs if it contains any at all. The main object of this note is to extend this result to complete k-graphs.