Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:56:21.326Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Deterministic and Asymptotic σ-Algebras of a Markov Operator

Published online by Cambridge University Press:  20 November 2018

Ulrich Krengel  and
Michael Lin
Ulrich Krengel
Affiliation:
Institut für Mathematische Stochastik, Lotzestrasse 13, D-3400 Göttingen, West Germany
Michael Lin
Affiliation:
Dept. of Mathematics and Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, Israel
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let P be a Markov operator on L∞(X, Σ, m) which does not disappear (i.e., P1A ≡ 0 => 1A ≡ 0 ) . We study the relationship between the σ-algebras

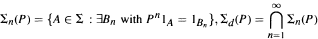
(the deterministicσ-algebra), and the asymptoticσ-algebra

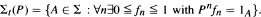
When m is a σ-finite invariant measure, 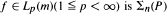measurable iff p*npnf = f, and also iff Pnf has the same distribution as f . The case of a convolution operator on a locally compact group is considered.

Keywords

60J0560J15:47A35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 32 , Issue 1 , 01 March 1989 , pp. 64 - 73
Copyright
Copyright © Canadian Mathematical Society 1989

References

1.[AB] Akcoglu, M. A. and Boivin, D., Approximation of Lp contractions by isometries, to appear.Google Scholar
2. Bougerol, [B] P., Une majoration universelle des fonctions de concentration sur les groupes localement compacts non-compacts. Proceeding conf. probability measures, Springer Lecture notes, 706, (1979), 36-40.Google Scholar
3. Derriennic, [D] Y., Lois “zéro ou deux” pour les processus de Markov. Applications aux marches aléatoires, Ann. Inst. Henri Poincaré (B) 12 (1976) 111–129.Google Scholar
4. Derriennic, [DL] Y. and Lin, M., Sur le comportement asymptotique des puissances de convolution d'une probabilité, Ann. Inst. Henri Poincaré (B) 20 (1984) 127–132.Google Scholar
5. Foguel, [FI] S. R., The ergodic theory of Markov processes, Van Nostrand Reinhold, New York, 1969.Google Scholar
6. [F2] Selected topics in the study of Markov operators, Carolina lecture series, Chapel-Hill, 1980.Google Scholar
7. Krengel, [K] U., Ergodic theorems, De Gruyter, Berlin-New York, 1985.Google Scholar
8. Krengel, [KL] U. and Lin, M., Order preserving non-expansive operators in L\, Israel J. of Math. 58, (1987), 170–192.Google Scholar
9. Lin, [LI] M., Mixing for Markov operators, Z. Wahr. verw. Geb. 19 (1971), 231–242. Google Scholar
10. [L2] Convergence of the iterates of a Markov operator, Z. Wahr. verw. Geb. 29 (1974), 153–163. Google Scholar
11. [L3] On weakly mixing Markov operators and non-singular transformations, Z. Wahr. verw. Geb. 55 (1981), 231–236. Google Scholar
12. [L4] Convergence of convolution powers of a probability on a LCA group, Semesterbericht Funktional analysis, Univ. Tubingen, (Winter 1982/3), 1–10.Google Scholar
13. Rosenblatt, [R] M., Markov processes. Structure and asymptotic behavior, Springer, Berlin- Heidelberg, 1971.Google Scholar
14. Woess, [W] W., Aperiodische Warhrscheinlichkeitsmasse auf Topologischen Gruppen, Monatsh. Math. 90 (1980), 339–345. Google Scholar