No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
In [2, page 3831], Varopoulos proves that for any ∈ > 0 there exists a function 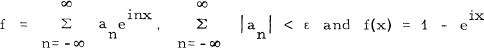 on a neighbourhood of 0. Indeed, if 0 < ∈ < π/2, then f(x) defined to be equal to 1 - e when -eix
on a neighbourhood of 0. Indeed, if 0 < ∈ < π/2, then f(x) defined to be equal to 1 - e when -eix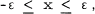 , linear on [∈, 2π - ∈] and of period 2π, is an example of such a function.
, linear on [∈, 2π - ∈] and of period 2π, is an example of such a function.
The above result can be used to give a direct proof of the following result without reference to the L2 theory [1, Theorem 2.6.4].