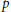Let $p$, 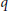$q$ be prime numbers with 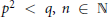${{p}^{2}}\,<\,q,\,n\,\in \,\mathbb{N}$, and $H$ a semisimple Hopf algebra of dimension 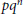$p{{q}^{n}}$ over an algebraically closed field of characteristic 0. This paper proves that $H$ must possess one of the following two structures: (1) $H$ is semisolvable; (2) $H$ is a Radford biproduct 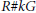$R\#kG$, where 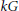$kG$ is the group algebra of group $G$ of order 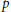$p$ and 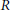$R$ is a semisimple Yetter–Drinfeld Hopf algebra in 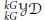$_{kG}^{kG}y\mathcal{D}$ of dimension 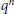${{q}^{n}}$.